局部非线性边界条件下热量方程解的空间渐近性

陈雪姣, 李远飞, 李宗锎

(广州华商学院 数据科学学院, 广州 511300)

0 引 言

关于热传导方程的Phragmén-Lindelöf型二择性研究目前已取得了很多结果[1-20]. 通常情况下, 这类问题定义一个半无穷的柱体为

R={(x1,x2,x3)|(x1,x2)∈D,x3>0},

其中D是坐标平面x1Ox2上的一个有界闭区域. 先假设方程的解在柱体R的侧面上满足零边界条件, 然后证明解随空间变量或者呈指数式(多项式)增长或者呈指数式(多项式)衰减. 例如: 文献[1]研究了一些热传导理论中伪抛物方程在零边界条件下解的空间二择性； 考虑到热量在柱体侧面上与外界发生热交换的情况, 文献[6]研究了调和方程

Δu=0, (x1,x2,x3,t)∈R×(0,T),

在边界条件

下的解空间二择性; 文献[7-8]对文献[6]的研究做了进一步推广; 文献[9]把上述研究推广到二元混合物中的热传导方程上; 文献[10]研究了带阻尼项的波动方程在半无穷柱体上解的空间二择性; 文献[11]进一步研究了波动方程在球体外部区域上解的空间爆破与衰减性质.

文献[15]考虑了瞬态调和方程在非线性动力边界条件下解的空间渐近性. 先把柱体的侧面分成两部分, 即∂D=Ω1∪Ω2,Ω1∩Ω2=Ø, 再假设解在Ω1和Ω2上分别满足不同的边界条件, 然后证明解的空间二择一性质. 受文献[15]的启发, 本文研究非标准条件下的热量方程：

其中

δ是一个大于零的常数. 本文假设存在大于零的常数C1, 使得

(6)

条件(6)可以满足, 例如可取f(u)为

f(u)=a1(2-cosu)u2p-1,

(7)

其中a1>0.

本文工作是对目前已有结果的进一步推广, 但与已有结果相比, 有几点不同： 1) 与文献[15]相比, 本文把解的二择一结果推广到非标准情形下； 2) 与文献[1]相比, 本文考虑了非线性边界条件, 因此, 文献[1]中成立的某些微分不等式在本文不再成立, 文献[1,15]的方法并不能直接应用到本文中, 文献[1]是本文结果的一个特例； 3) 本文把已有结果进一步推广到更一般的抛物方程中.

1 主要结果

令Dz表示R在x3=z处的横截面, 即

Dz={(x1,x2,x3)|(x1,x2)∈D,x3=z}.

令Rz表示R的一个子集, 即

Rz={(x1,x2,x3)|(x1,x2)∈Dx3,x3≥z≥0}.

显然,R0=R,D0=D.此外, 记

Ω1(z)=Ω1×{z},Ω2(z)=Ω2×{z}.

引理1[16]如果u是一个光滑函数,D是二维空间中的一个有界区域, 则存在大于零的常数C2, 使得

首先建立一个辅助函数

(8)

在式(8)中利用散度定理和方程(1)-(5), 可得

其中z0是x3轴上的一个点. 对式(9)微分, 可得

通过对函数E(z,T)进行分析, 可得以下二择一定理.

定理1设u为方程(1)-(5)在一个半无穷柱体R上的解, 其中f(u)满足式(6),δ2>1. 则或者

成立, 或者

成立, 其中β1是大于零的常数.

注1定理1表明, 当z→∞时方程(1)-(5)的解或者指数式增长或者指数式衰减.

定理2设u为方程(1)-(5)在一个半无穷柱体R上的解, 其中f(u)满足式(6),δ2=1. 则或者

(13)

成立, 或者

(14)

成立, 其中c4,β2和Q0是大于零的常数.

此时需要限定时间长度T、参数δ及区域Ω2, 使得

成立, 再结合式(10)可得

利用与定理1和定理2类似的方法可得解的二择一定理.

注3由Q0的定义可知, 要使式(12)和(14)有意义, 必须推导-E(0,T)的上界. 采用与文献[7-8,15]类似的方法可得以下定理.

定理3设u为方程(1)-(5)在一个半无穷柱体R上的解, 其中f(u)满足式(6)及

(15)

则有

-E(0,t)≤C,

其中C是大于零的常数.

2 主要结果的证明

2.1 定理1的证明

对于式(16), 存在以下两种情形.

E(z,T)≥E(z0,T)>0,z≥z0>0.

由式(16)可得

即

(17)

对式(17)从z0到z积分, 可得

(18)

再结合式(9)可得式(11).

情形2) 如果对任意的z>0, 均有E(z,T)<0. 此时由式(16)可得

即

(19)

对式(19)从0到z积分, 可得

(20)

结合式(20),(21)可得式(12). 证毕.

2.2 定理2的证明

由于δ2=1, 所以式(9),(10)可以写为

(22)

(23)

此时, 重新计算式(16), 可得

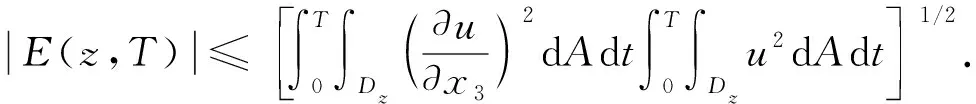
(24)

利用引理1和Schwarz不等式, 可得

其中M1=[t·measure(Ω2)]1/2. 利用式(6), 可得

其中M2=[t·measure(Ω2)]p/(p-1). 将式(26)代入式(25), 可得

(28)

对于式(28), 存在以下两种情形.

情形1) 如果存在一个点z0>0, 使得E(z0,T)>0, 与上述分析类似可得E(z,T)≥0, ∀z≥z0. 所以式(28)可以写为

(29)

利用Young不等式, 可得

(30)

把式(30)代入式(29), 可得

(31)

(32)

对式(32)从z0到z积分, 可得

在式(33)中舍弃不等式左边的非正项, 可得

(34)

(35)

式(35)表明E(z,T)随z→∞指数式增长. 再结合式(20)即可完成式(13)的证明.

情形2) 对任意的z≥0, 均有E(z,T)<0. 此时由式(28),(30)可得

(36)

类似式(32), 可得

(37)

对式(37)从0到z积分, 可得

注意到-E(z,T)≤-E(0,T), 所以在式(38)中舍弃最后两项, 可得

(39)

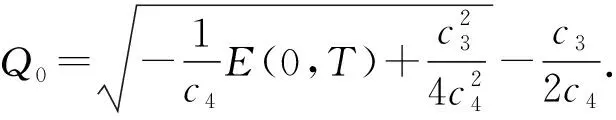
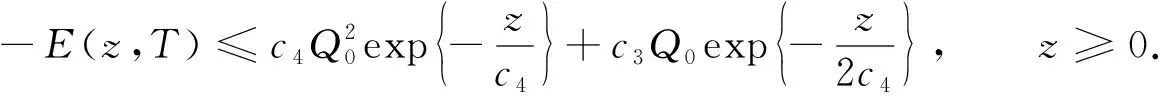
(40)

(41)

结合式(40),(41)可得式(14). 证毕.

3 模型推广

考虑二元混合物中的热量方程, 该模型适用于层状复合材料的热传导问题[21], 文献[22-23]对该模型做了进一步的讨论和推广. 文献[3]得到了非标准条件下二元混合物中热量方程的解在R上的空间衰减估计, 其中假设解在柱体的边界上满足齐次Dirichlet条件; 文献[9]研究了二元混合物中热量方程在侧面上满足非齐次Neumann条件的情形, 得到了解的二择性. 与文献[3,23]不同, 本文考虑局部非线性条件下解的渐近性.

二元混合物中的热量方程可以写为

其中k1,k2,b1,b2,δ1,δ是大于零的常数.

在式(45)中, 函数f1(u)和f2(v)满足

(48)

其中C3,C4>0,q1,q2>1.

为得到解二择一定理, 首先建立辅助函数:

(49)

利用散度定理和方程组(42)-(47), 可得

采用与主要结果证明中类似的方法, 可得：

(51)

对式(51)进行类似的分析, 可得以下定理.

定理4设u为问题(42)-(47)在一个半无穷柱体R上的解, 其中f1(u),f2(v)满足式(48),δ2>1. 则或者

成立, 或者

成立, 其中β3是大于零的常数.

定理5设u为问题(42)-(47)在一个半无穷柱体R上的解, 其中f1(u),f2(v)满足式(48),δ2=1. 则或者

成立, 或者