n阶多时滞微分方程的周期解

李文金, 庞彦尼

(1. 吉林财经大学 应用数学学院, 长春 130117; 2. 吉林大学 数学学院, 长春 130012)

0 引 言

时滞微分方程在生物数学、工程、经济、信息等领域应用广泛, 可用于描述动物血红细胞再生、种群生态系统、心脏起搏等现象. 目前, 关于微分方程振动理论及其应用的研究已有很多成果[1-7], 特别是关于二阶微分方程的研究已有较大进展, 但对于微分方程中含有多时滞量, 用上下解的单调迭代技巧处理其周期解的存在性和唯一性的研究文献报道较少.

考虑n阶时滞微分方程

-u(n)(t)=f(t,u(t),u(t-τ1),u(t-τ2),…,u(t-τn)),t∈

(1)

ω-周期解的存在性, 即满足方程(1)和u(t+ω)=u(t)的解, 其中f:×n+1→连续且关于t以ω为周期,τ1,τ2,…,τn为正常数. 本文利用单位算子扰动理论, 通过建立新的极大值原理, 讨论方程(1)ω-周期解的存在性和唯一性. 本文结果推广了文献[1]中二阶多时滞微分方程

-u(2)(t)=f(t,u(t),u(t-τ1),u(t-τ2),…,u(t-τn)),t∈

ω-周期解的存在性.

1 预备知识

记Cω()是以ω为周期的全体连续函数按范数构成的Banach空间. 对()是以ω为周期的m阶连续可微函数全体按范数构成的Banach空间. 记()是Cω()中的非负函数锥. 设Mn为正常数, 且

根据文献[8]中引理2.4知, 微分算子Lnu=u(n)+Mu在周期边界条件下满足极大值原理, 且有下列引理.

引理1[8]设M∈(0,Mn)为一个常数, 则n阶线性边值问题

存在唯一解Φ∈Cn[0,ω], 且对∀t∈[0,ω],Φ(t)>0.

引理2[9]设M∈(0,Mn), 则对∀h∈Cω(),n阶线性微分方程

-u(n)(t)+Mu(t)=h(t),t∈

(2)

存在唯一ω-周期解

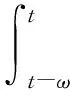
(3)

且解算子S:Cω()()是线性全连续算子.

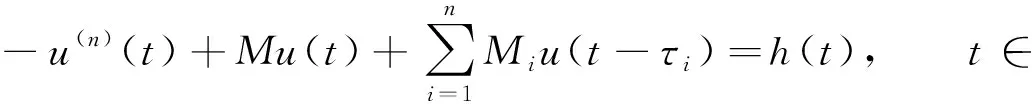
(4)

周期解的存在性, 其中M>0,Mi≥0.

引理3线性方程(2)的ω-周期解算子S:Cω()→Cω()具有下列性质:

1) 范数‖S‖=1/M;

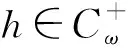
证明: 1) 由S的定义可知,

即‖S‖≤1/M.

另一方面, 取h0=1, 则h0∈Cω(), ‖h0‖C=1, 且于是有

(5)

故性质1)成立.

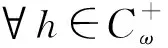
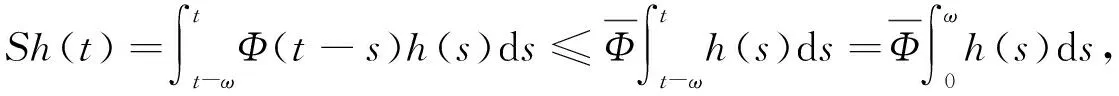
(6)

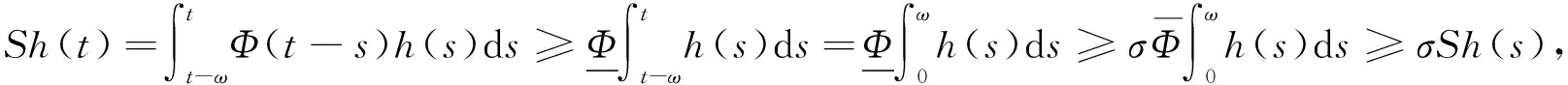
(7)

故性质2)成立. 证毕.

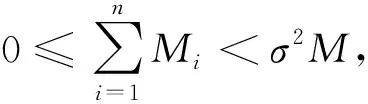
证明： 由线性方程ω-周期解的表示式(3)知,u∈Cω()是方程(4)的ω-周期解当且仅当

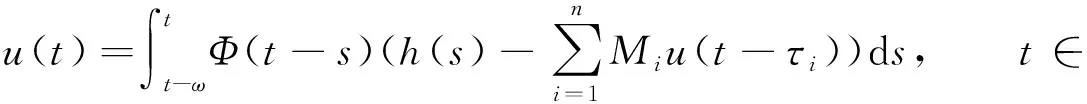
(8)

定义算子B:Cω()→Cω()为

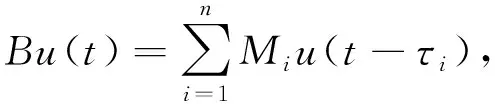
(9)

则B:Cω()→Cω()为正的有界线性算子, 易知结合式(3),(8),(9), 有

(I+SB)u(t)=Sh(t),t∈.

(10)

由单位算子扰动理论可知,I+SB为有界线性逆算子：

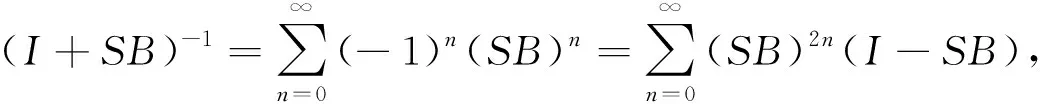
(11)

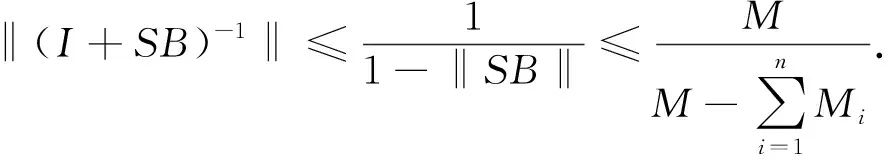
(12)

因此算子方程(10)有唯一解

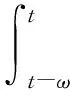
(13)

其为方程(4)的ω-周期解. 由式(3)知,S:Cω()→Cω()是线性全连续算子, 由(I+SB)-1的有界线性可知,T=(I+SB)-1S是全连续的. 由式(11)～(13)可得

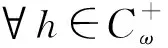
因此(I-SB)S是正的, 即T:Cω()→Cω()是一个正算子. 证毕.

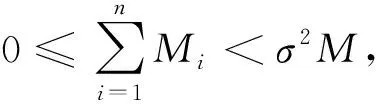
则u(t)≥0,t∈.

证明： 令

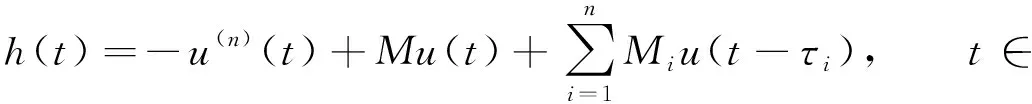
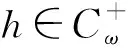
为利用单调迭代技巧, 类似周期边值问题上下解的概念[10], 本文引入方程(1)上下ω-周期解的定义.

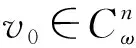
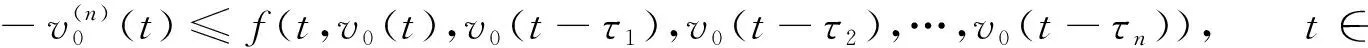
(14)

则称v0是方程(1)的下ω-周期解; 若上述不等号取反向, 则称v0是方程(1)的一个上ω-周期解.

2 主要结果

定理1设f:×n+1→连续, 关于t以ω为周期, 且v0和w0是方程(1)的下ω-周期解和上ω-周期解,v0≤w0,v0≤Qv0,Qw0≤w0, 则方程(1)在v0和w0之间存在最小ω-周期解和最大ω-周期解, 且可分别以v0,w0为初始元作迭代得到.

若f在v0和w0之间还满足以下条件:

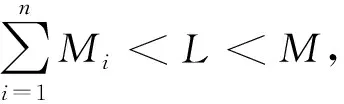
则方程(1)在v0和w0之间存在唯一解u*.

证明： 令D=[v0,w0]={u∈Cω()|v0≤u≤w0}. 定义算子F:D→Cω()为

于是F:D→Cω()连续、有界, 且为增算子. 则方程(1)在D中的解等价于算子Q=T∘F:D→Cω()有不动点, 且由F的序增性及T的线性和正性可知Q=T∘F是增算子, 即对∀u1,u2∈[v0,w0], 满足u1≤u2, 则Qu1≤Qu2.

对Q用增算子不动点定理单调迭代求解. 下面分三步证明.

1) 证明算子Q在D中有不动点. 分别以v0,w0为初始元作迭代序列:

vn=Qvn-1,wn=Qwn-1,n=1,2,….

(15)

根据算子Q的单调性, 有

v0≤v1≤v2≤…≤vn≤…≤wn≤…≤w2≤w1≤w0,

(16)

则{vn}和{wn}分别在序区间D上单调递增和单调递减. 由Q的紧性可知, {vn},{wn}⊂[v0,w0]为Cω()中的相对紧集, 有一致收敛的子列. 因此{vn}和{wn}均在Cω()中收敛, 即(), 使得又因为D为Cω()中的凸闭集, 故在式(15)中令n→∞, 则由Q的连续性知,所以和都是算子Q在D中的不动点.

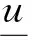
vn≤u*≤wn.

(17)

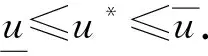
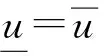
则

‖wn-vn‖C≤(M-L)n·‖Tn‖·‖w0-v0‖C.

(18)

由于{vn}和{wn}在Cω()中分别单调递增收敛到及单调递减收敛到所以在式(18)中, 当n→∞时, 有从而即u*是方程(1)在方程v0和w0之间的唯一解. 证毕.