一类受白噪声扰动群聚模型的动力学行为
张艳妮, 周 冉, 陈霄雨
(1. 吉林建筑科技学院 基础科学部, 长春 130114; 2. 吉林大学 数学学院, 长春 130012; 3. 海军航空大学青岛校区 基础教研室, 山东 青岛 266041)
0 引 言
群聚现象也称为协调运动[1-2], 在生物、物理、化学及社会经济系统等领域普遍存在. 例如: 冬季南飞的大雁以一致的速度向同一方向飞行; 鱼群、羊群向相同方向结群运动; 人类语言由呼叫声和肢体语言向语言的演化等[3-5]. Vicsek等[6]从统计物理的角度首次提出了描述动物群体行为的数学模型; Cucker等[7]基于简单的速度匹配思想建立了如下Cucker-Smale模型(简称C-S模型):
其中:λ表示耦合强度, 当λ>0时表示第i个和第j个个体相互吸引, 当λ<0时表示第i个和第j个个体相互排斥;aij(t)表示第i个和第j个个体之间相互作用, 计算公式为
Ha等[8-9]研究了一类具有加性白噪声的随机C-S模型, 证明了在给定的模型结构下不会出现强群聚现象; Ahn等[10]考虑一类具有乘性白噪声的随机C-S模型, 在权重函数有非负下界的条件下, 证明了系统呈强随机群聚行为.
本文主要考虑如下具有乘性白噪声扰动的随机种群模型:

(1)
其中: (xi,vi)∈2d,xi(t)和vi(t)分别表示第i个个体在t时刻的位置和速度状态;λ>0表示耦合强度;Ψ(|xj-xi|)是衡量个体间相互影响的交流权重函数,Ψ(s)是单调不增的C1类函数;D≥0表示噪声强度; dW(t)表示白噪声, 其期望为0, 且〈dW(t)·dW(t*)〉=δ(t-t*), 〈 〉表示求期望;gi(v)dW(t)是乘性白噪声,gi(v)=vi-ve,ve是d中的常向量.
定义1如果系统(1)的任何解(xi(t),vi(t))(i=1,2,…,N)都满足下列条件:
则称系统(1)呈强随机群聚行为.
本文研究系统(1)的强随机群聚行为. 首先, 考虑两个个体的群聚模型强随机群聚行为; 其次, 对N个个体群聚模型(1), 在交流权重函数有正下界的条件下, 证明其呈强随机群聚行为.
1 无条件群聚
下面考虑N=2的情形, 此时系统(1)可简化为如下方程:
其中Ψ12=Ψ21=Ψ(|x2-x1|). 令x(t)=x1(t)-x2(t),v(t)=v1(t)-v2(t), 则

(2)

引理1设(x,v)是系统(2)的解, 则有

(3)
其中v0=v(0)=v1(0)-v2(0).

从而式(3)成立. 证毕.
定理1设λ>0,Ψ(s)>0, 则存在正常数Tε和TM, 使得当t>max{Tε,TM}时, 有
证明: 由重对数律得
故对任意ε>0, 存在Tε>0, 使得当t>Tε时, 有
注意到
故对任意M>0, 存在TM>0, 使得当t>TM时, 有
因此, 当t>max{Tε,TM}时, 有|W(t)|≤(1+ε)Mt.
选取ε,M使得
代入式(3)可得所证结论.

2 一般群聚模型分析
令

于是, 系统(1)可分解为大尺度系统

(4)
和微尺度系统

(5)
首先, 考虑大尺度系统(4). 注意到d(vc-ve)=D(vc-ve)dW(t), 由It公式得
积分得
其中C为常数. 从而
命题1存在T>0, 使得(xc,vc)满足下列条件:
1) 〈vc(t)-ve〉=vc(0)-ve, 〈xc(t)-xc(0)〉=vc(0)t,t>0;
3) |xc(t)-(xc(0)+tve)|≤C(T,D)|vc(0)-ve|,t>T.
证明: 2)显然成立, 下面证明1)和3).

于是
同理可得
〈xc(t)-xc(0)〉=vc(0)t.
3) 注意到

故
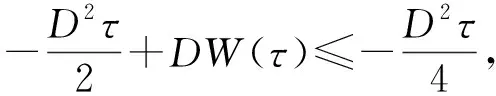
|xc(t)-(xc(0)+tve)|≤C(T,D)|vc(0)-ve|.
证毕.

其次, 考虑微尺度系统(5).



(8)
注意到
故有
由Hölder不等式可得
即

(10)


(11)


(12)
证明: 设Ψ(s)≥Ψ*>0,s∈(0,+∞). 由式(11)得

(13)

结合式(13)得
记C1(N,k,c)≜C(N,k)·ck/2, 则
(14)
将式(14)两边积分得
再取对数得式(12)成立. 证毕.


(15)

于是
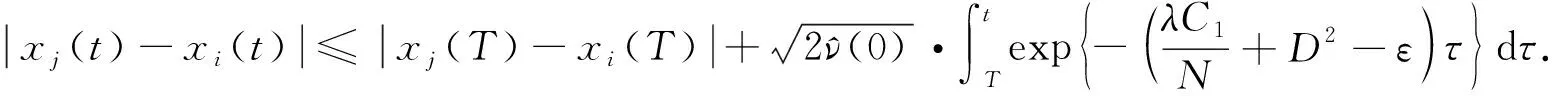
(16)
由式(15),(16)知, 模型(1)呈强随机群聚行为.

