带有Riemann初值简化色谱方程组的初边值问题
刘冬冬, 俞康宁, 郭俐辉
(1. 新疆大学 数学与系统科学学院, 乌鲁木齐 830046; 2. 昌吉学院 数学系, 新疆 昌吉 831100)
0 引 言
色谱法作为一种高效的分离和分析技术, 广泛应用于化学和工程领域, 其能将样品中不同的组分迅速分离, 并逐一分析. 色谱理论模型是数学物理领域中的重要组成部分, 目前已得到广泛关注. 本文考虑简化色谱方程组

(1)
的初边值问题
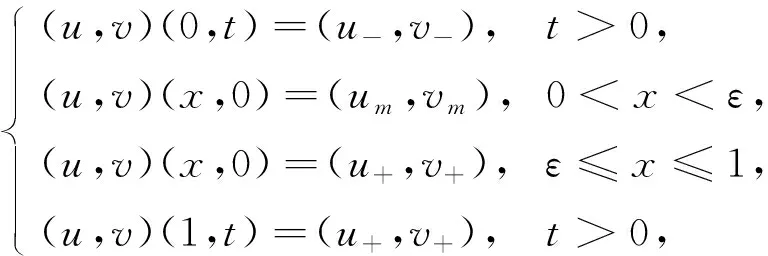
(2)
其中(u-,v-),(um,vm),(u+,v+)为常状态, 且u≥0,v≥0. 方程组(1)可由

(3)
经过变量替换u=u1+u2,v=u1-u2得到, 其中u1和u2表示两种溶液的浓度.
目前, 关于色谱方程组和Dirac激波相关性质的研究已取得很多结果[1-11]. 例如: Shen[1]通过特征线法和波的相互作用得到了方程组(3)Riemann解的稳定性; Li等[2]利用黏性消失法研究了简化色谱方程组(1)当-1 (4) 的Riemann问题. 特别地, 当u=0时, 其两个特征值为1, 因此在相平面(u,v)中, 方程组(1)当u=0时是抛物退化的. 关于双曲方程初边值问题的研究也得到广泛关注[12-14]. 特别地, Joseph等[15]研究了基于Riemann初值的边值问题, 在假设初边值位于其中一个Riemann不变量的水平集上, 构造了非守恒弹性动力学方程组的精确解; Yao等讨论了双曲守恒律方程组的初边值问题, 根据边界熵不等式得到了边界x=0处初边值问题的解[16], 之后又得到了双边界初边值问题的解[17]. 上述研究结果表明, 在经典意义下, 色谱方程组的初边值问题是不适定的, 即方程组的解既不存在也不唯一, 从而需要给出合适的边界熵不等式. 本文考虑简化色谱方程组的初边值问题, 通过找到合适的边界熵条件, 根据基本波及Dirac激波在边界上的相互作用, 利用边界熵不等式使初边值问题(1)-(2)的解存在且唯一. 下面简要介绍简化色谱方程组(1)-(4)的Riemann问题, 详细过程参见文献[6]. 方程组(1)-(4)的基本波为疏散波 (5) 和激波 (6) 以及接触间断 (7) 由式(5),(6)知疏散波曲线与激波曲线共线, 故方程组(1)属于Temple类型[18]. 当u+>u-=0时, 可得到具有奇异性的Dirac激波解, 在分布意义下Dirac激波解满足广义Rankine-Hugoniot条件: (8) 根据基本波的性质, 可将方程组(1)-(4)的初值问题分为以下3种情形: 1) 0≤u+ 下面通过选择方程组(1)的熵流对, 利用黏性消失法给出弱熵解(u,v)(x,t)在x=1处的边界熵不等式[19]. 考虑带有黏性项的色谱方程组 (9) 其中 (10) 对任意熵流对(η,q)[19-20], 满足 qT=ηTf′(u,v), (11) (12) 在分布意义下, 方程组(1)在{(x,t)|x>0,t>0}中存在解(u,v), 使得对每个熵流对都满足熵不等式: η(u,v)t+q(u,v)x≤0. (13) 因此, 根据熵不等式(13)可得边界处的充分条件: 边界熵不等式. 综上, 可得: 定理1在边界x=1处, 对任意t>0和熵流对(η,q), 初边值问题(1)-(2)在x=1上的取值(u,v)(1-,t)与边界值(u+,v+)(1,t)满足边界熵不等式: (14) 本文只推导了边界x=1处的边界熵不等式, 边界x=0处类似. 定义1对于空间中的任意状态(u+,v+), 对每个熵流对(η,q)均满足 (15) 的状态(u,v)所构成的集合, 称为边界上可容许解的集合L(u+,v+). 根据定义1, 初边值问题(1)-(2)的边界熵条件可表示为 (u,v)(1-,t)∈L(u+,v+),t>0. 由Kruzkov熵流对[20]可知方程组(1)的熵流对满足 (16) 对任意固定状态(u+,v+), 由边界熵不等式(15)可得 将式(17)简化为 (18) 若k不在u和u+之间, 则不等式(18)恒成立. 因此, 可得如下两个性质. 性质1边界x=1上的可容许解(u,v)满足集合 L(u+,v+)={(u,v)|u-k≤0,k∈[u,u+]}, 或者 L(u+,v+)={(u,v)|u-k≥0,k∈[u+,u]}. 性质2边界x=0上的可容许解(u,v)满足(u,v)(0,t)=(u-,v-). 下面讨论简化色谱方程组(1)-(2)的初边值问题. 考虑利用文献[3]具有3个常状态初值的方法, 求解方程组(1)具有3个初值 (19) 的Riemann问题, 这里0<ε≤1. 通过验证方程组(1)-(19)的Riemann解在{(0,t)|t>0}和{(1,t)|t>0}上是否满足边界熵条件, 得到初边值问题(1)-(2)的解, 表示为(u,v)(x,t)=(u,v)(x,t)|Γ1, 其中Γ1={(x,t): 0≤x≤1,t>0}. 注1对于x=1处的边界值, 根据ε=1,ε<1以及1在相互作用点的不同位置, 利用边界熵不等式, 可得初边值问题(1)-(2)的解. 下面分别对0≤u+ 情形1) 0=um 由于um=0,u-,u+>0, 从(ε,0)发出Dirac激波. 当u->um=0时,R1的前向波与J1在直线x=t处重合, 即J1的左状态是(0,0), 如图1所示. (20) (21) 公民在民主程序中的表意行为是有偏好倾向的,这种倾向对民主价值是减损的,甚至是负面的,这是民主不可回避的问题。从古代到革命时代都是如此,特别是自毁式偏好和不道德的偏好影响了民主的价值体现。民主偏好的存在不仅影响到公民民主意识的形成,也影响到了公民和政府的良性互动。传统的研究已经充分认识到了公民意志表达的这种缺陷,但是没有改变这种状态的进路,至少在“互联网”之前都是如此。 则 (22) 显然成立. 由于式(21)也是初值问题(1)-(20)在Dirac函数支撑下的弱解, 因此易证明方程组(1)的第一个方程成立. 将式(21)代入方程组(1)的第二个方程, 当t>t′时, 在分布意义下, 有 (23) 由性质1和性质2可知, 初边值问题(1)-(2)的解分为ε=1和ε<1两种情形. 当ε>1时, 边界熵不等式不成立. 当ε=1时, 通过边界熵不等式,x=0和x=1处初边值问题(1)-(2)的解可表示为 (24) 当ε<1时, 考虑相互作用点位置x′,x″与1的大小关系, 可得初边值问题(1)-(2)的解如下: 当ε<1 (25) 当x′=1时, 初边值问题(1)-(2)在x=0和x=1处的解与ε=1一致; 当x′<1时, 初边值问题(1)-(2)在x=0和x=1处的解为 (26) 情形2) 0 如图2所示, 当t很小时, 初值问题(1)-(19)的解可表示为 图2 当0 根据性质1和性质2, 初边值问题(1)-(2)的解可为如下两种形式: 当ε=1时, 根据边界熵不等式, 边界x=0和x=1上的初边值问题(1)-(2)的解为 (27) 当ε<1时, 考虑到相互作用点x′, 对于ε<1 对于x′=1,x′<1 情形3) 0 如图3所示, 初值问题(1)-(19)的解可表示为 图3 当0 当t充分大时, 初值问题(1)-(19)的解可表示为 同理, 基于性质1和性质2, 可构造多种情形下初边值问题(1)-(2)的解. 当ε=1时, 边界x=0和x=1处初边值问题(1)-(2)的解可表示为 (28) 当ε<1时, 通过考虑相互作用点位置x′,x″与1的大小关系, 对于ε<1 对于1=x′,x′<1 下面利用迎风格式模拟[22]的数值结果验证初边值问题(1)-(2)理论分析的正确性. 本文仅对情形1)、情形2)和情形3)中ε=1和ε<1的情形进行数值模拟, 其余情形类似, 其中时间t=3.6 s. 例1给定初值 (u-,v-)=(6,2), (um,vm)=(0,3), (u+,v+)=(5,5). 图4 当ε=1时情形1)中初值问题(1)-(19)中u和v值Fig.4 Values of u and v of initial value problem (1)-(19) when ε=1 in case 1) 则情形1)当ε=1时的数值模拟结果如4和图5所示, 当ε=0.5时的数值模拟结果如图6和图7所示. 由图4和图5可见, 初值问题(1)-(19)与初边值问题(1)-(2)在区域[0,1]内有相同的解. 由图6和图7可见, 初值问题(1)-(19)与初边值问题(1)-(2)的解完全相同. 例2给定初值 (u-,v-)=(4,1), (um,vm)=(5,5), (u+,v+)=(3,4), 图5 当ε=1时情形1)中初边值问题(1)-(2)中u和v值Fig.5 Values of u and v of initial boundary value problem (1)-(2) when ε=1 in case 1) 图6 当ε=0.5时情形1)中初值问题(1)-(19)中u和v值Fig.6 Values of u and v of initial value problem (1)-(19) when ε=0.5 in case 1) 图7 当ε=0.5时情形1)中初边值问题(1)-(2)中u和v值Fig.7 Values of u and v of initial boundary value problem (1)-(2) when ε=0.5 in case 1) 图8 当ε=1时情形2)中初值问题(1)-(19)中u和v值Fig.8 Values of u and v of initial value problem (1)-(19) when ε=1 in case 2) 则情形2)当ε=1时的数值模拟结果如图8和图9所示, 当ε=0.4时的数值模拟结果如图10和图11所示. 由图8~图11可见, 初值问题(1)-(19)与初边值问题(1)-(2)的解完全一致. 例3给定初值 (u-,v-)=(1,3), (um,vm)=(3,2), (u+,v+)=(5,4), 则情形3)当ε=1时的数值模拟结果如图12和图13所示, 当ε=0.6时的数值模拟结果如图14和图15所示. 由图12~图15可见, 初值问题(1)-(19)与初边值问题(1)-(2)的解完全一致. 图9 当ε=1时情形2)中初边值问题(1)-(2)中u和v值Fig.9 Values of u and v of initial boundary value problem (1)-(2) when ε=1 in case 2) 图10 当ε=0.4时情形2)中初值问题(1)-(19)中u和v值Fig.10 Values of u and v of initial value problem (1)-(19) when ε=0.4 in case 2) 图11 当ε=0.4时情形2)中初边值问题(1)-(2)中u和v值Fig.11 Values of u and v of initial boundary value problem (1)-(2) when ε=0.4 in case 2) 图12 当ε=1时情形3)中初值问题(1)-(19)中u和v值Fig.12 Values of u and v of initial value problem (1)-(19) when ε=1 in case 3) 图13 当ε=1时情形3)中初边值问题(1)-(2)中u和v值Fig.13 Values of u and v of initial boundary value problem (1)-(2) when ε=1 in case 3) 图14 当ε=0.6时情形3)中初值问题(1)-(19)中u和v值Fig.14 Values of u and v of initial value problem (1)-(19) when ε=0.6 in case 3) 图15 当ε=0.6时情形3)中初边值问题(1)-(2)中u和v值Fig.15 Values of u and v of initial boundary value problem (1)-(2) when ε=0.6 in case 3) 综上, 本文基于黏性消失法建立了边界熵不等式, 由初值问题(1)-(19)的Riemann解结合边界熵不等式得到了初边值问题(1)-(2)当ε=1和ε<1的解, 并利用数值模拟进一步验证了理论分析的正确性.
1 预备知识





2 边界熵不等式







3 两点初边值问题


















4 数值模拟