聚焦度量过程，感悟面积本质

张明

【摘 要】从度量的角度认识“量”的本质，贯穿整个小学阶段，从长度、面积，到角度、体积在数学知识内容和学习方法上都具有内在的联系。本文以“量面积”的活动为主线，从长方形的面积到其他图形的面积，在不同测量对象的变化中进一步加深学生对面积本质的认识。

【关键词】面积本质 度量 单元整体教学

一、教学设计思考

“面积”是北师大版数学三年级下册第五单元的内容，开展“量面积”活动的教学是我们在进行“面积”单元统整时设计的第2课时。从内容来讲，本节课涵盖了原教材“长方形的面积”这一内容，是学生在前一课时初步认识面积和面积单位的基础上，以长方形、正方形为研究对象，进一步从度量的角度进行“面”的大小刻画，理解面积本质。同时，本节课也是本单元继续学习面积单位换算和面积相关应用的重要基础。从知识之间的整体联系来看，本节课与之前学习的长度的度量，以及后续要学习的角度、体积的相关知识，在学习方式上具有一致性;长方形的面积知识也是后续其他平面图形，如平行四边形、三角形、梯形、圆形等面积度量转化的基础。

作为承前启后的一节课，怎样让学生既能从知识内容上感受前后联系，从度量角度加深对面积本质的进一步认识，又能在学习方法上进行迁移，感受学习方式的一致性呢？结合学情调研和教学实践分析，基于单元统整的理念，在教材整合和教学重构方面，我们进行了如下的思考与尝试。

（一）突出“量”的活动，感悟度量本质

测量是将测量对象和标准单位进行比较的过程。学生在前一节课的学习中已经能用面积单位“铺满”图形的方式度量图形的面积。本节课继续聚焦“量”面积的活动，从长方形、正方形入手，拓展至其他学生认识的平面图形，在“量”的活动中，进一步理解面积的本质是面积单位的累加，即测量对象内部包含的面积单位的多少。

（二）沟通“量”的方法，理解公式本质

基于教学前测和教学实践经验，教师未教授相关知识之前，有些学生就已经知道长方形面积=长×宽，以及学习后容易将“长方形面积=长×宽”与“长方形周长=（长+宽）×2”混淆，是学习长方形面积这一内容时，常遇到的问题。究其原因，学生感到困难的从来都不是测量的结果，而是学生未能很好地从“量”的方法上，建立起长、宽与内部所包含面积单位数量之间的联系。因此，本节课力求引导学生升级“量”的方式，实现从铺满，到不铺满，再到公式计算的过渡，理解面积公式是“数”法（面积单位）优化的结果，建立起一维“长、宽”和二维“面积”之间的对应和联系。

（三）丰富“量”的素材，积累活动经验

三年级学生思维正处在由具体形象思维向抽象逻辑思维逐渐过渡的发展阶段，这样的思维特点决定了其对长方形面积的探究过程，还是需要借助一定的直观“测量”活动，才能到达最后合理抽象公式进行推理计算。有效的数学活动经验，应该要能促进有效的数学思考。在安排“量”的素材时，教师既要考虑对象的丰富性，如量长方形、正方形，以及其他平面图形时，也要考虑方式的多样性，如铺满“量”、不铺满“量”、想象“量”，满足不同学生的能力需求，引导学生积累“量”面积的活动经验，实现长方形面积刻画从形象到抽象，从直觉到推理的过程。

（四）变换“量”的对象，实现方法迁移

长方形的面积探究，是学生从度量角度感悟面积本质的一个例子和应用，同时也是后续学习其他图形面积的基础。因此，本节课还要注意揭示知识的纵横联系，在进行不同图形“量”面积的活动时，教师要引导学生在不同的图形变换的基础上思考其中的不变，促进学生对“图形的度量”整体知识网络的建构和学习方法的迁移。同时也注重从统整的视角审视整个小学阶段的“测量”教学，帮助学生建立学习长度、面积、角度以及体积等知识的整体框架。

基于以上思考，我们将本课的学习目标定位为：在升级“量”法、优化“数”法的过程中，探究并理解长方形的面积公式;在“量”更多平面图形面积的过程中，发展学生的空间观念、培养学生的知识迁移能力，从度量角度进一步理解面积的意义，引导学生在探究交流中发展数学表达能力，建立“测量”的数学知识网络。

二、教学过程

环节一：探究长方形的面积

活动1：挑战激趣，升级“量”

（1）量一量：长方形的面积是多少

师：上节课我们认识了什么是面积，同学们了解了选择不同的面积单位，在图形上铺满，就能知道这个图形的面积是多少。这节课我们继续研究长方形的面积（板书：量长方形的面积），不过难度要升级了——不铺满！你能知道长方形的面积是多少吗？

生：能！

课件呈现活动要求。

选一选：选择一种学习材料（每组提供1张长方形的纸、1把直尺、1平方厘米的小正方形若干）。

铺一铺：一眼看出你的测量方法。

填一填：长方形的面积是多少。

师：老师收集了一些同学的作品，看看大家是怎样“不铺满”，也能知道长方形面积的。

学生作品展示：

（2）说一说：测量面积的方法和结果

师：请同学们看一看以上作品，并说一说。

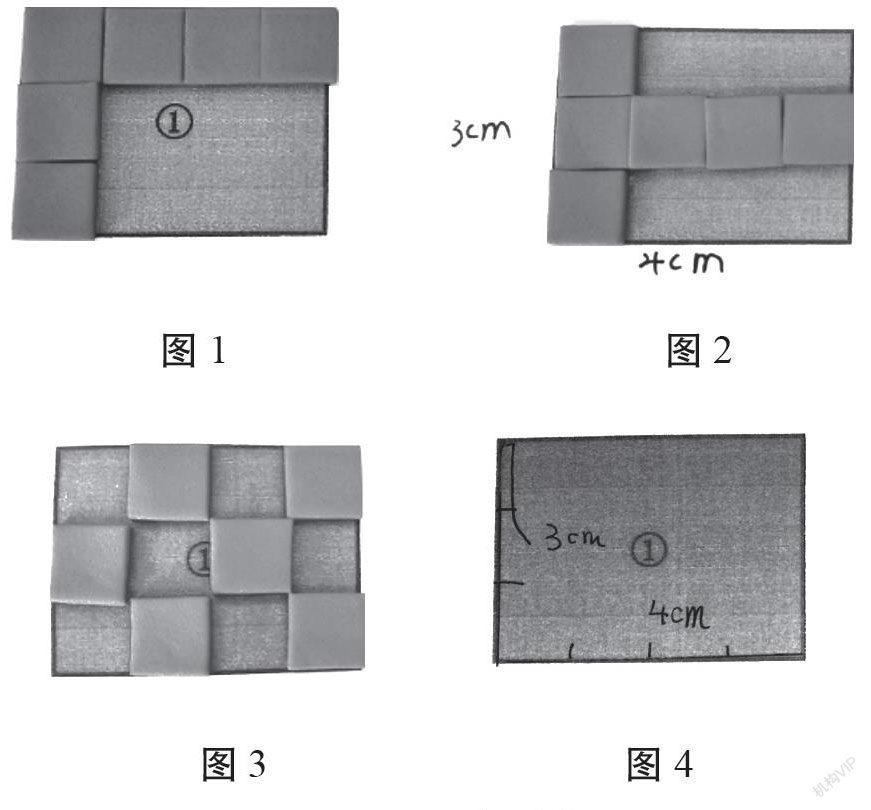
生1：图1把第一排铺好了，铺了4个1平方厘米的小正方形，一共有3行，3×4=12，一共是12个1平方厘米的小正方形，也就是12平方厘米。

生2：圖2和图1其实是一样的，只要把图1中第一行的4个1平方厘米的小正方形移了下来，就是图2。所以图2也可以用3×4=12，得出长方形纸的面积是12平方厘米。

生3：图3虽然没有铺满，但是每一个空的地方都相当于一个1平方厘米的小正方形，我们通过想象填上去的话，也是一行有4个，一共有3行。

师：如果把图3中没有铺上去的小正方形添上去，一行也有4个1平方厘米的小正方形，能铺3行，一共12个。谁还有其他的方法吗？

生4：我来说图4，宽是3厘米，平均分成3段，长是4厘米，平均分成4段，再用3×4，就可以得出12平方厘米。

师：图4都没有铺，你是怎样看出是12平方厘米的？4代表什么？3又表示什么意思？

生：4表示长方形的长边上能摆4个1平方厘米的小正方形，宽边上能摆3行，一共就是3×4=12（平方厘米）。

[设计意图]围绕“量”字开启教学，激活学生度量学习的活动经验，并在此基础上升级“量”法挑战，激发学生探究的兴趣和学习需要。

活动2：交流沟通，理解“量”

师：同学们想到了这么多升级后的“量”法，都知道了这个长方形纸的面积是12平方厘米。老师把大家的方法放大了展示到黑板上（贴板书），这些方法之间有什么联系吗？

生：都可以用3×4=12，长方形的面积是12平方厘米。

师：既可以用3乘4，也可以用4乘3，这里的4代表什么？3代表什么呢？

生1：4代表长方形的长，3代表长方形的宽。

生2：4代表长方形的长，表示能铺4平方厘米，3代表长方形的宽，表示能铺3个1平方厘米，铺满的话就是4×3=12（平方厘米）。

师：（结合黑板上板书）你们的意思就是说，原来需要铺满才能知道面积，现在只需要知道一行有几个这样的小正方形，一共有几行就能知道面积。或者说只要知道长边上有几个这样的面积单位，宽边上有几个这样的面积单位就可以了。所以长方形的面积，我们还可以怎样计算？

生：4×3=12。

（师板书12=4×3）

师：4是什么？3是什么？也就是长方形的面积可以用……

生：长方形的面积=长×宽。

（师板书）

师：在这几种方法中，你都能找到长方形的面积等于长乘宽吗？

师指名学生找一找，说一说。

[设计意图]展示学生不同的“量”面积的方式，从“不铺满”测量面积的方式中，优化“数”面积单位的方法，找到长、宽与长方形所包含面积单位个数之间的对应关系，理解公式的本质。

活动3：丰富素材，想象“量”

师：用升级后的玩法，如果1格表示1平方厘米，你能快速说出下面这些长方形的面积是多少吗？

课件逐一出示下面的长方形，指名学生说一说。

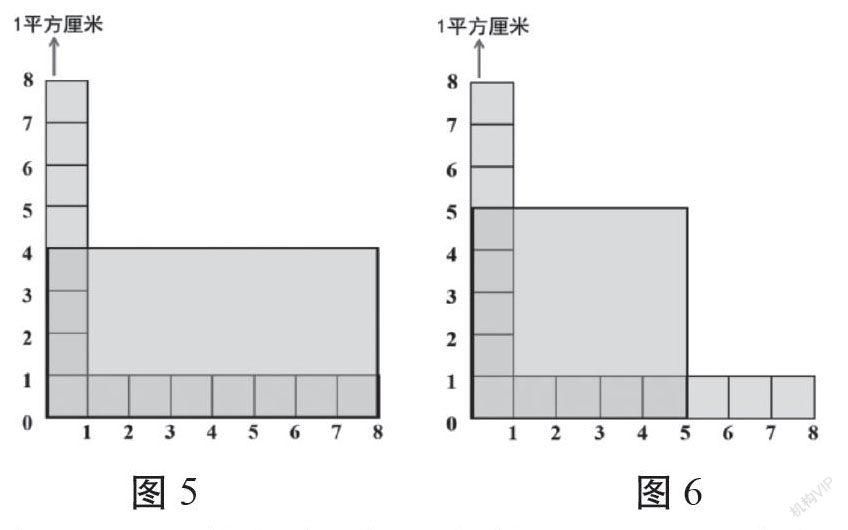
生1：图5是长方形，面积是8×4=32（平方厘米），8代表一行有8个1平方厘米，共4行，面积是32平方厘米。

生2：图6中，一行有5个1平方厘米，共5行，面积是5×5=25（平方厘米）。

师：图6也是一个正方形，所以正方形的面积可以怎样简化算呢？

生：正方形面积=边长×边长。

（师板书）

环节二：探究其他图形的面积

活动4：变换图形，拓展“量”

（1）尝试操作

师：真厉害！这么快就完成了长方形、正方形面积测量方法的升级，接下来我们继续升级，你们敢接受挑战吗？你们还能测量出更多图形的面积吗？（板书：更多图形）猜一猜，我们可能要挑战测量哪些图形的面积？

生：三角形、平行四邊形、梯形……（见图7）

课件出示：

活动要求：

标一标，画一画：一眼看出你的测量方法;

填一填：图形的面积是多少？

生独立完成挑战卡，小组内交流，每人挑战一个，快速完成的同学可以申请再挑战一个图形。

（2）汇报交流

师：我们一起来看看同学们是怎样测量的。

①平行四边形。

生1：我把平行四边形上多出来的一部分切下来，移到左边，刚好拼成了一个长方形（见图8）。

生2：我也是这样拼接的，拼起来之后变成了长4厘米、宽3厘米的长方形，面积可以用4×3=12（平方厘米），见图9。

师：切下来，补过去，是个好办法！由平行四边形变成了长方形，形状变了，但是什么没变？

生：面积没变。

师：哦，同学们把平行四边形的面积转化成了长方形的面积，真不错。

②三角形。

生1：我是把三角形里面两个半格的小三角形拼在一起，就是1个1平方厘米整格。4个半格的小三角形刚好拼成2个整格，还有6个原本就是整格的，一共8平方厘米（见图10）。

生2：我觉得这整个三角形像是大正方形的一半，正方形的面积是4×4=16平方厘米，一半刚好是8平方厘米（见图11）。

③梯形。

图12 图13

生1：我在多出来的那个部分画上了格子，大概是4个格子的一半，也就是2格。其余的部分是4×3=12 （格），一共是14平方厘米（见图12）。

生2：我和他的方法差不多，我把多的部分分出来，就是一个三角形，面积应该是2平方厘米，其余部分是12平方厘米，加起来也就是梯形的面积14平方厘米（见图13）。

（3）小结思考

师：同学们，当我们需要测量不规则的图形面积时，你们都想到了哪些好办法？

生1：可以数一数图形中有几个格子，就能知道面积是多少平方厘米。

生2：可以把多出来的部分切下来，移过去补上，转化成我们会算的图形。

生3：2个半格的可以拼在一起算一格。

……

师：是的，我们可以用割补的方法，拼一拼、凑一凑，把不好测量的图形转化成我们会测量的长方形，再计算面积。

[设计意图]长方形面积是后续学习多边形面积计算和转化的基础，引导学生变化图形，“量”其他平面图形的面积，在操作中直观让学生初步体会，不管哪种平面图形，其面积都是要看所包含单位面积的个数，不是整格的可以进行拼一拼、补一补，初步体会转化思想。

环节三：课堂小结，前后整合

师：同学们，上节课我们从原来的“量长度”到“量面积”。这节课，我们对测量长方形面积的方法进行了升级，还研究了测量更多图形面积的方法。现在你对“量面积”有什么体会呢？

生1：可以把不规则的转化成规则的图形。

生2：“量面积”时要知道里面有多少个小方格。

生3：不一样的图形，只要分一分、补一补，就能变成规则的图形。

……

师：除了量线段的长度、量面的大小，以后我们还会学习量角的大小，量体积的大小。今天的学习，对你们有什么启示吗？

生1：在以后的学习中也会用到今天学过的方法。

生2：我觉得用今天学习的方法解题会比较轻松。

生3：以后量角或体积的话，应该有更小或更大的单位。

……

师：同学们，让我们带着今天“量面积”过程的学习方法和思考，共同期待后续的学习吧！

[设计意图]“图形度量”的教学贯穿于小学阶段，从一维的长度到二维求面积，再到三维求体积，以及角度的刻画，在内容、数学思维以及学习方式上都具有密切的联系，因此在教学时，不能管中窥豹只见一斑，要引导学生树立“度量”学习的全局观，加强知识的前后联系思考，促进整体知识网络的建构。

三、课后反思

长方形的面积教学，内容主线清晰明了，为什么不上成一节传统课，用量一量、摆一摆归纳面积公式，应用公式解决问题呢？反正最终也是要让学生掌握面积计算公式。为什么还要大张旗鼓“量面积”？分析这节课，我们觉得最大的特点是，通过有效的数学操作活动，促进了学生对面积本质的数学思考。

（一）聚焦联结，合理组织学习活动

为什么学生会出现混淆周长和面积的情况？为什么高年级学生学习多边形面积时容易混淆公式？究其原因是学生对面积的本质理解不到位。学生除了认识面积之外，真的没有其他学习面积的数学活动经验了吗？其实不然，长方形的面积属于“图形度量”的教学，与长度测量一脉相承。教师只有正确把握学情和知識间的联系，才能对本节课有合理的目标定位，组织以“量”为主线的学习活动，实现从度量角度理解把握面积本质的目的。

（二）问题驱动，恰当优化操作策略

操作活动是积累数学活动的重要途径。整节课聚焦“量面积”活动，学生充分地经历了“长方形面积”直观测量的过程。积累活动经验的目的是为了促进学生有效地数学思考。为什么“长方形的面积=长×宽”？“长×宽”究竟是在计算什么？在问题驱动下，实现长方形的面积从具体直观的“量”到借助数学抽象推理的“不量”，也即利用面积公式计算面积。

（三）拓展联系，有效促进深度学习

史宁中教授认为，度量是人的本能，即我们先天具有感知数量多少和距离远近的能力。因此，即使多边形面积、角度、体积等内容的学习安排在三年级以后，也需要我们在学习面积之初，就树立“结构化”“整体化”的意识。根据学生的学习能力、认知需求以及生活经验，进行有针对性的前延后拓，合理迁移，才能有效促进学生对于“度量”知识的整体建构，让深度学习发生。