基于最大应变能密度幅值的胎圈疲劳寿命预测方法*

曹雷天，王国林**，梁 晨，柏 林，王伟斌

(1.江苏大学 汽车与交通工程学院，江苏 镇江 212013；2.建大橡胶(中国)有限公司，江苏 昆山 215300)

随着仿真技术的发展，有限元仿真分析的方法逐渐应用在有关轮胎疲劳耐久的研究中。在轮胎开发阶段如果能够准确地评估轮胎在实际使用过程中的疲劳寿命(Nf)，将大大降低企业的研发成本，缩短研发周期。

目前已经发展出了众多结合有限元仿真预测轮胎的疲劳寿命的方法，如基于连续力学产生的基于应变、应力和能量的方法等[1]。国内外学者也使用不同方法对轮胎疲劳寿命进行了研究：Pidaparti等[2]使用有限元分析研究了由帘线-橡胶复合材料疲劳引起的裂纹形式的断裂破坏，证明了裂纹类型、载荷和裂纹尺寸对J积分的值有很大影响；Yan等[3]使用应力分析参数方法和断裂力学方法研究轮胎结构参数对子午线卡车轮胎关键区域应力参数的影响，并预测了带束边缘耐久性能；Previati等[4]利用最大应力、最大应变、应变能密度(SED)、J积分等方法预测带束层边缘的寿命并证明了这些方案的有效性；Kim[5]通过有限元法的稳态滚动分析和带束层边缘区域橡胶化合物的Nf方程，建立了基于SED的系统方法来预测与速度相关的失效行驶距离；Nyaaba等[6]247-249采用开裂能量密度理论来预测巨型轮胎的裂纹成核寿命。

我国在轮胎疲劳分析领域也做了大量研究工作，陈洛兵[7]采用SED最速下降法成功预测了胎圈疲劳裂纹扩展方向。徐振[8]基于ABAQUS有限元分析软件对轮胎耐久性能进行了分析，通过提取帘线材料的应力确定了钢丝帘线的危险区域。姜明磊[9]基于断裂力学理论，建立不同裂纹尺寸的局部模型，计算裂纹尖端J积分并采用Nf公式计算轮胎Nf。谢熠萌[10]基于裂纹扩展方法，通过疲劳实验获取了目标橡胶材料破坏撕裂能、裂纹扩展速率等疲劳参数，并通过仿真获得应力-应变历史并准确预测了轮胎耐久寿命。刘悦[11]以轮胎耐久性为主要考量，确定了胎面耐磨性和胎肩耐疲劳性能两个目标函数，建立轮胎优化模型。优化方案较初始设计方案的耐久性能提升超过20%。程钢等[12]分析了侧倾角对轮胎接地区中心截面SED分布的影响，从而为提高轮胎耐久性能提供了理论依据。何川[13]基于虚拟裂纹闭合技术开发自定义疲劳断裂单元，成功预测带束层部位和胎圈部位的Nf。

从上文可以看出目前不同预测轮胎寿命的方法均具有一定的有效性。由于大部分子午线轮胎实际的破坏区域是以胎肩区域为主，针对胎圈区域进行寿命预测相对较少，而本文的研究对象则是以胎圈破坏为主，所以需要确认一种可以用于胎圈Nf预测的方法。由于在工程实践中SED应用广泛，根据Abraham等[14]的研究，SED比基于应变的预测参数更为有效、准确，本文采用基于应变能密度幅值(ΔSED)的方法预测轮胎胎圈区域Nf。

1 有限元模型的建立与验证

1.1 有限元模型的建立

为使轮胎有限元模型有更高的精度，根据公司提供的轮胎断面实物制作了断面夹具并进行了断面扫描,如图1所示，将扫描结果导入CAD中绘制轮胎结构，然后导入Hypermesh中绘制网格，如图2所示。

图1 轮胎断面实物及夹具

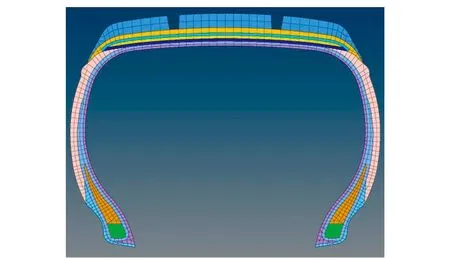
图2 二维有限元模型

各部分橡胶材料参数采用单轴拉伸实验获得，如图3所示，使用Yeoh本构模型拟合材料参数，帘线部分采用目前公认的描述帘线橡胶复合性能的rebar单元，轮辋和路面定义为刚性。应用ABAQUS中的*SYMMETRIC MODEL GENERATION命令将二维网格模型旋转成三维网格模型，整个模型共有92 800个单元，114 300个节点，如图4所示。

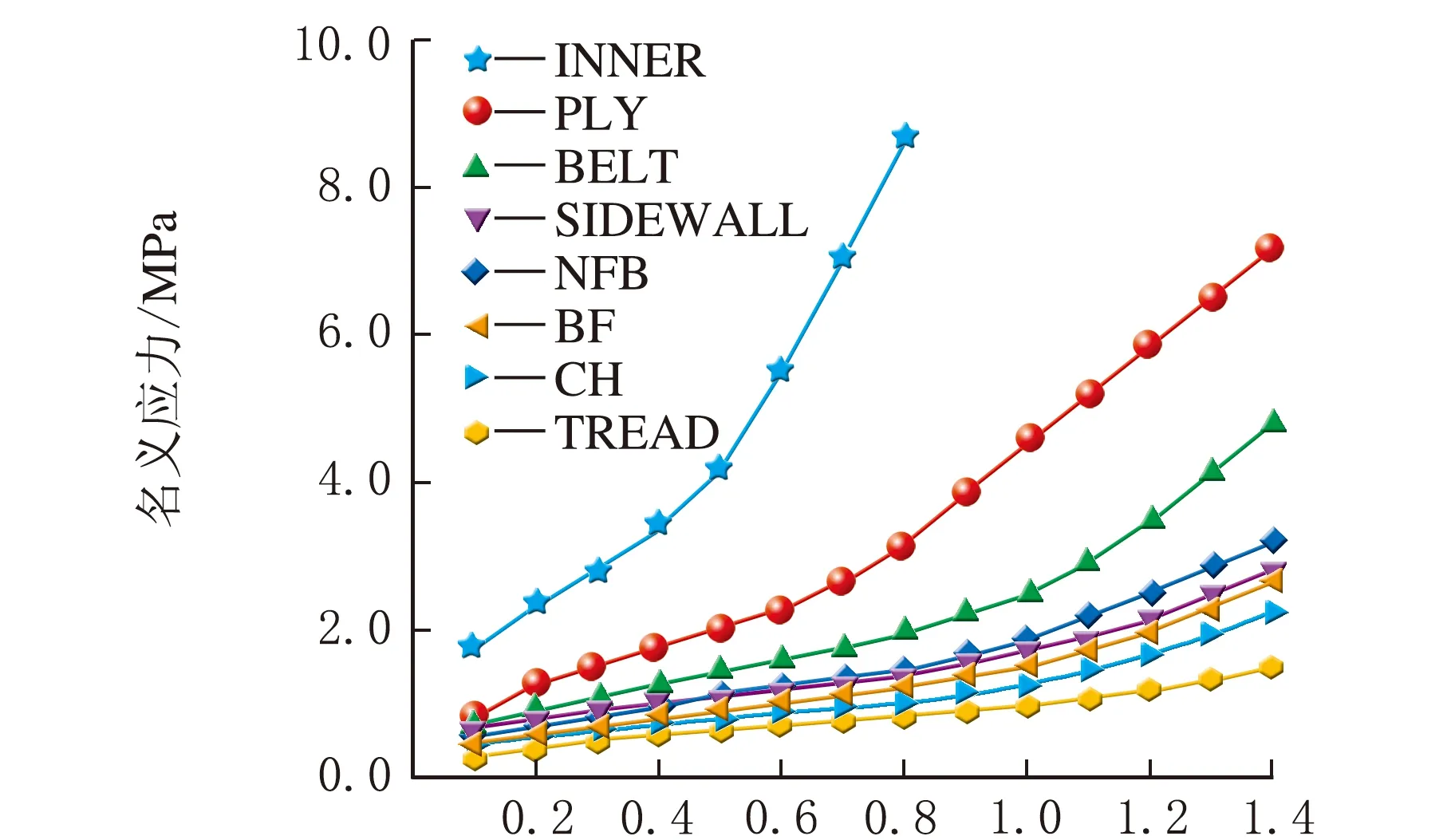
名义应变/%图3 不同胶料的应力应变响应曲线

图4 三维有限元模型

1.2 有限元模型的验证

在建立完成三维有限元模型后，将轮胎和轮辋进行过盈装配，再进行充气，充气完成后施加径向载荷。为了简化模型以便于问题的分析，本文将轮辋和路面定义为解析刚体。轮辋安装完成后，对轮胎内衬层施加0.55 MPa的均布压力，以模拟轮胎充气过程，施加的载荷为17 468 N，摩擦模型选用库伦模型，加载过程如图5所示。

图5 加载过程

本文利用ABAQUS提供的一种隐式算法模拟轮胎在转鼓路面的自由滚动，自由滚动的速度和耐久性实验的速度保持一致，滚动速度设定为40 km/h。通过插值求出当轮胎与地面的摩擦力恰好为0时的临界角速度，轮胎自由滚动角速度大小为35.96 rad/s，方向为顺时针；并设定转鼓逆时针转动，角速度大小为13.11 rad/s。

根据GB/T 23663—2009标准，对轮胎进行径向刚度测试。轮胎的径向刚度实验在GT-LT-5000型轮胎综合强度实验机上进行。测试前需将轮胎胎压调整为额定气压0.55 MPa，在室温环境下预置24 h后再进行刚度测试。载荷工况与也有限元仿真时保持一致，对轮胎施加径向载荷，并记录轮胎径向位移与径向载荷的关系曲线，如图6所示。

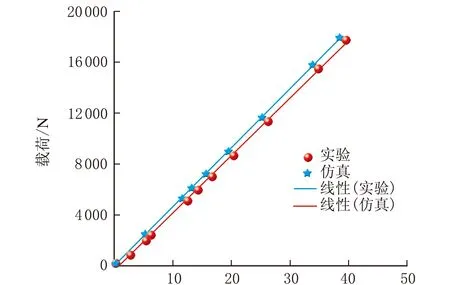
径向变形/mm图6 径向刚度特征曲线

由图6可知，仿真结果与实验数据具有良好的一致性，证明所建的有限元模型计算精度高，可用于后续轮胎胎圈的疲劳仿真研究。

2 轮胎胎圈疲劳寿命预测

2.1 试样制备

为了得到胶料关于ΔSED的Nf方程，需通过实验获得胎圈各胶料ΔSED和Nf的曲线。为此利用EKT-2102-DF疲劳实验机对胎圈附近胶料进行了单轴拉伸疲劳实验。试样的尺寸和形状根据GB/T 1688-2008(硫化橡胶伸张疲劳的测定)标准设计,试样长度为100 mm，厚度为2 mm,如图7和图8所示(单位，mm)。

为减少Nf数据分散而导致获取的Nf曲线的误差，结合实验标准，在同一加载工况下，采用5个哑铃形试样进行实验，取Nf的平均值。

根据1.2中有限元仿真计算结果和硫化橡胶伸张疲劳测定标准，每一种胶料的最大应变设置如表1所示。实验的环境温度为(23±2)℃。为了方便计数和避免突发故障，使用摄像头对实验过程进行监测。当同组实验的所有试样完全断裂时，停止实验。

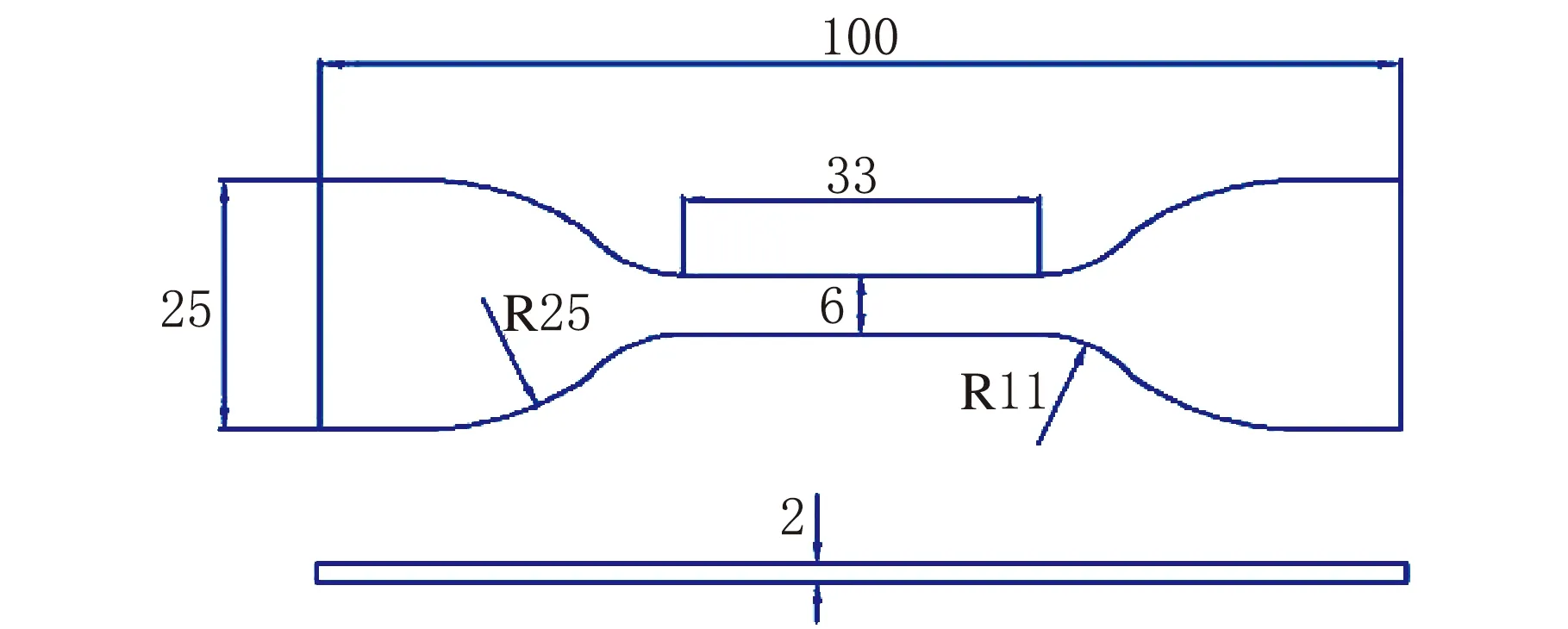
图7 试样几何尺寸

图8 哑铃状试样

表1 各胶料实验应变

2.2 实验结果处理

表2为3种胶料在不同最大应变下的Nf结果。

欲绘制3种胎圈胶料的ΔSED与Nf的ΔSED-Nf曲线，得出基于ΔSED的Nf方程，还需要求出胶料在不同最大应变下的ΔSED。

SED是材料的应力-应变曲线包含的面积，单位为MJ/m3。在ASTM-D4482-07(国际橡胶性能-拉伸循环疲劳实验方法标准)中[15]，提供了计算橡胶试样拉伸实验SED的方法。这种方法需要根据试样拉伸获得的应力应变数据，绘制出试样的应力-应变曲线，来计算每条曲线包含的面积，进而可以得出不同胶料在不同应变下的SED。

表2 3种胶料在不同最大应变下的Nf

胎体层胶、三角胶、耐磨胶的应力-应变关系曲线由静态加载下的单轴拉伸实验获得，结果如图9所示。

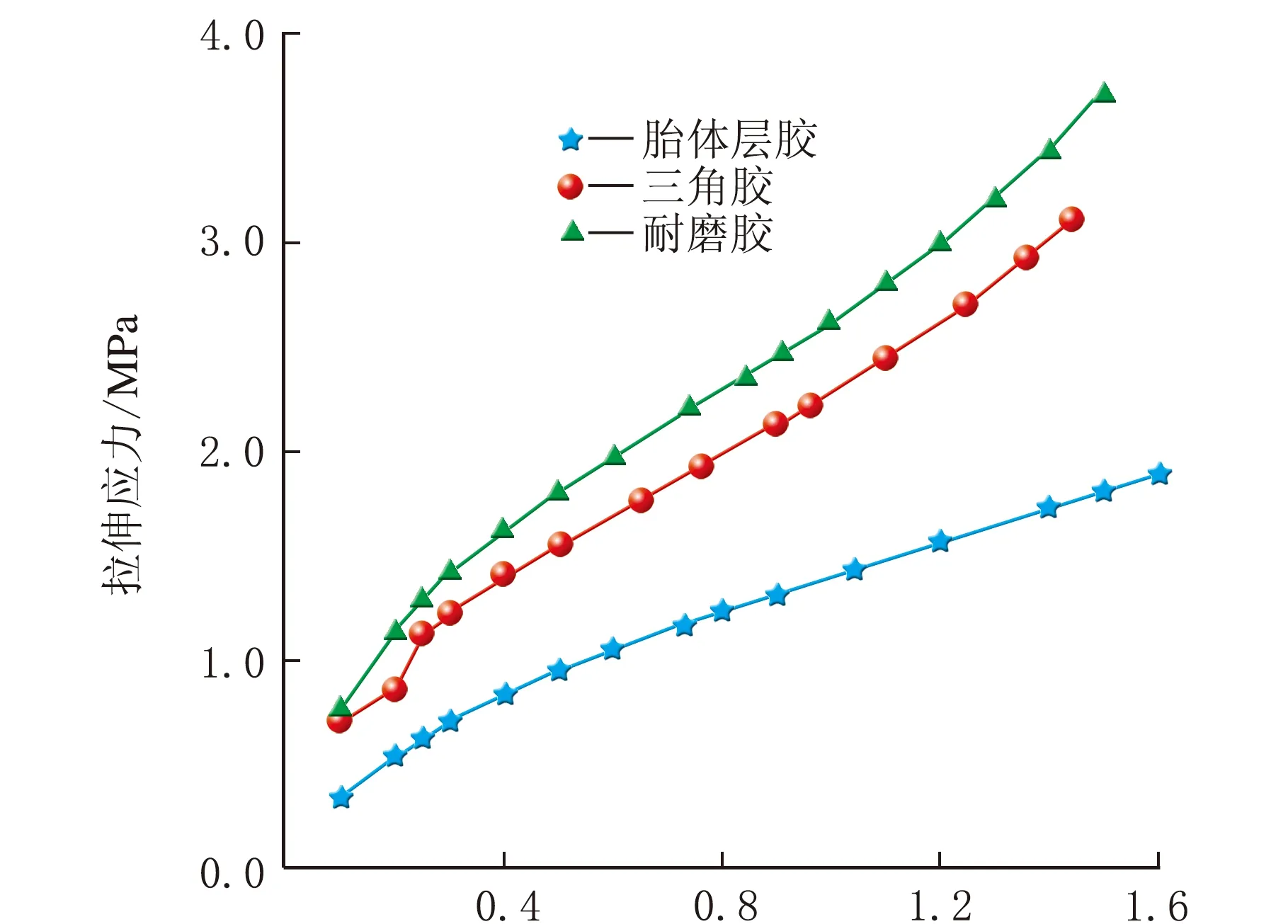
应变/%图9 3种胎圈胶料的应力-应变曲线

本文利用ASTM-D4482-07推荐的Simpson公式法计算不同应变下的SED，如式(1)所示。由于循环实验的最小SED都为0，故最小SED也都为0，因此试样的ΔSED即为不同应变下的SED。

(1)

式中：a为最小应变；b为最大应变。

计算整理后，得出3种胎圈胶料在不同最大应变下的ΔSED，如表3所示。

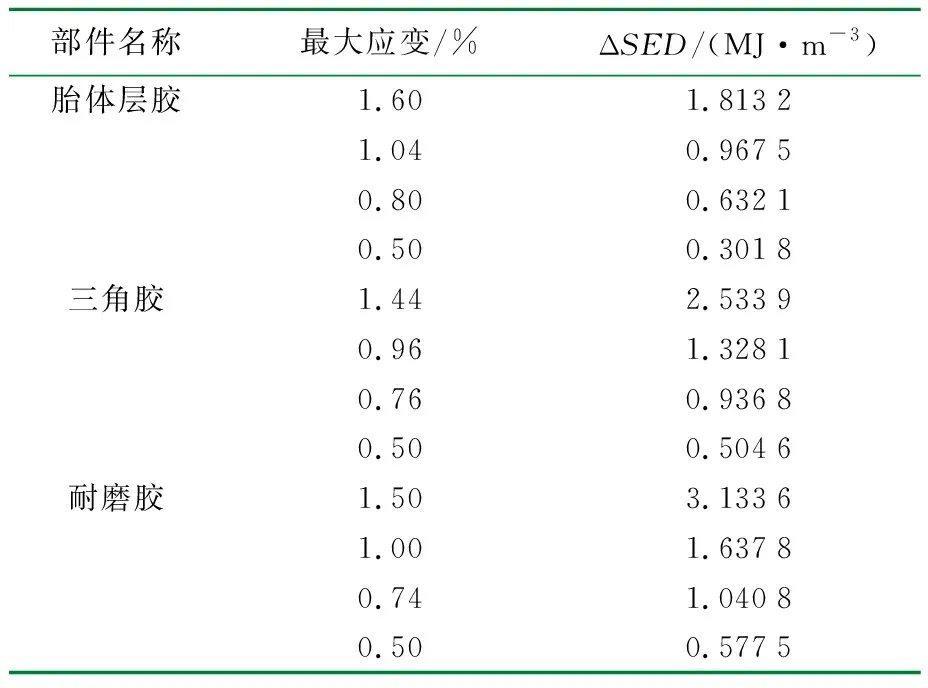
表3 3种胶料在不同最大应变下的ΔSED

2.3 胶料Nf方程

根据2.2中处理得到的3种胎圈胶料试样在不同最大应变下的ΔSED与Nf，分别绘制出的胎圈胶料的ΔSED-Nf曲线如图10所示。

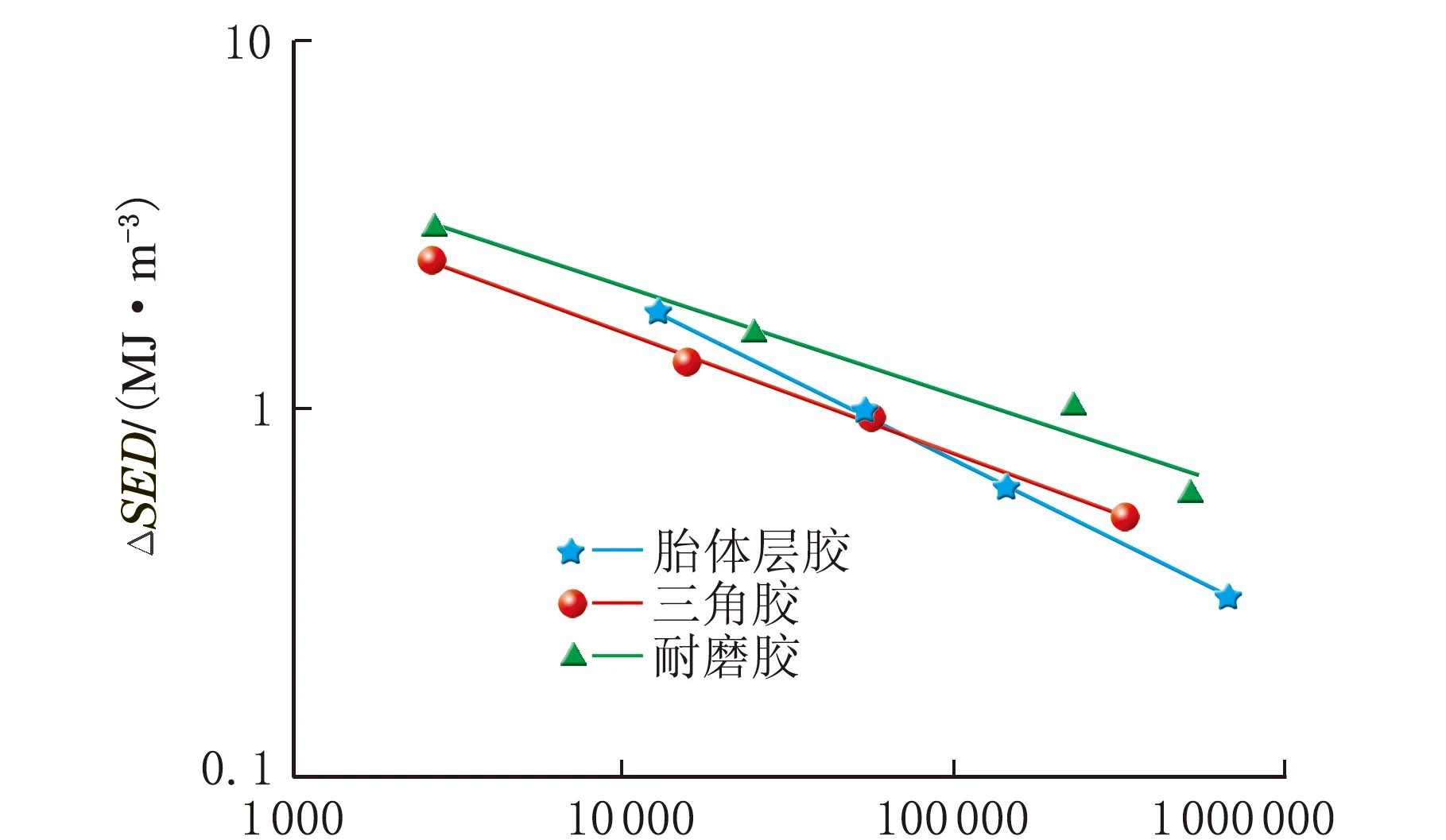
Nf/次图10 3种胎圈胶料ΔSED-Nf曲线

对图10的实验数据进行拟合，得出的胶料的Nf方程，如式(2)～式(4)所示。

(2)

(3)

(4)

为方便后续Nf的计算，对式(2)～式(4)进行形式上的简单转换，便得到了这3种胶料的基于ΔSED的Nf方程，如式(5)～式(7)所示。

胎体层胶的Nf方程为：

Nf=49220(ΔSED)-2.22

(5)

三角胶的Nf方程为：

Nf=42788(ΔSED)-3.04

(6)

耐磨胶的Nf方程为：

Nf=140 691(ΔSED)-3.4

(7)

2.4 轮胎Nf预测

根据1.2中有限元仿真分析得出的胎体层胶、三角胶和耐磨胶3种胶料的SED分布情况求得最大应变能密度幅值(ΔSEDmax)，分别代入Nf方程式(5)～式(7)中，即可测得这3种胎圈胶料在胎压为0.55 MPa，负载为17 468 N，速度40 km/h的工况下的Nf。通过式(8)可以将Nf转换成轮胎胎圈的疲劳行驶距离。

Df=2πR×Nf

(8)

式中：Df轮胎胎圈的疲劳行驶距离；R为轮胎的自由滚动半径。

这3种胎圈胶料的Nf和Df预测结果如表4所示。

表4 各胶料的Nf和Df预测结果

由表4可以看出，对于研究目标175/75R14型轮胎而言，在充气压力为0.55 MPa,实验速度40 km/h,负荷为17 468 N时，三角胶的Nf最短，胎体层胶的Nf预测结果和三角胶较为接近，耐磨胶的Nf最长。因此，胎圈部位的Nf受三角胶料的影响最大，当轮胎承受长时间的循环载荷时，三角胶由于Nf较短，最早发生疲劳破坏，可以基于三角胶的Nf方程对175/75R14型轮胎的胎圈Nf进行大致预测。

为了验证上述预测方法的可靠性和准确性，在GC-YLSN-1114型轮胎耐久性转鼓实验机上对现行方案的175/75R14型轮胎进行了耐久性实验。实验工况：充气压力为0.55 MPa,实验速度为40 km/h,负荷为17 468 N。实验转股直径为1.707 m，在常温下进行实验，取4次实验平均值作为疲劳实验的结果，轮胎疲劳破坏形式为胎圈裂。预测值与实验结果对比如表5所示。

表5 预测Df与实验Df

由表5和式(8)可知，胎圈Df预测值与实际疲劳实验获得的Df误差较大，为进一步验证该预测方法的有效性，修改了部分轮胎结构参数(三角胶高度、反包高度)如表6所示，设计了3种断面结构不一致的轮胎。分别对3种轮胎进行耐久性实验与Nf预测。耐久实验仍进行4次，取平均值作为疲劳实验的结果，并确认轮胎的破坏区域为胎圈，结果见表7。

表6 断面结构修改结果对比

表7 不同断面方案预测Df与实验Df对比

由表7可知，虽然预测Df与实验Df相差较大，但是预测Df与实验Df的关系较为明显，实验Df是预测Df的4.27～4.56倍之间，取平均值4.39重新计算预测Df，结果见表8，可得误差最大为3.9%，具有良好的一致性，说明了这种预测胎圈疲劳Df方法的可靠性，可以应用于轮胎胎圈疲劳寿命的预测。对于预测Df与实验Df相差较大这一情况，通过一些学者的研究[16]可以确定原因之一是由于胶料在测定Nf的单轴拉伸实验中的最小应变与轮胎实际运行中产生的最小应变不符，即本研究采用单轴拉伸实验中最小应变为0。即最小载荷为0，而非零载荷的单轴拉伸实验会产生应变结晶效应，从而改善橡胶的拉伸强度，进而使橡胶部件的Nf提高数倍甚至一个数量级[6]250-252。通过仿真结果可以确认，本文所分析的轮胎三角胶部分存在最小应变，由此可以确认，本研究所用最小应变为0的单轴拉伸实验获得的材料参数来预测胎圈区域Nf是导致预测值偏小的原因之一。

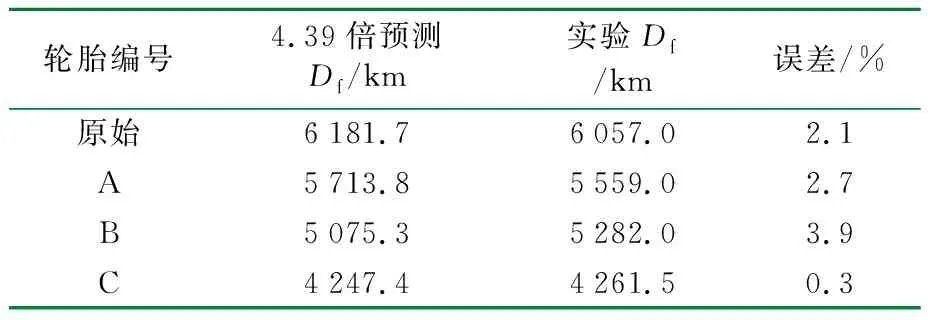
表8 预测Df与实验Df的误差对比

3 结 论

以175/75R14型轻卡子午线轮胎为研究对象，首先建立了轮胎有限元模型，并利用径向刚度实验对比验证了模型的有效性。根据单轴拉伸循环实验得出了各个胎圈胶料的Nf，结合应力应变数据，得出了不同最大应变下的胶料ΔSED。对实验数据处理后分别绘制了胎体层胶、三角胶、耐磨胶的ΔSED-Nf曲线，拟合得出了3种胎圈胶料的基于应ΔSED的Nf预测方程，并预测得出了3种胎圈胶料的Nf。结果表明三角胶的Nf最短，因而胎圈部位的Nf受三角胶料的影响最大，可以基于三角胶的Nf方程对175/75R14型轮胎的胎圈Nf进行大致预测。

为验证这种方法的有效性，进行了耐久性实验。发现实验Df与预测Df差距较大，为进一步验证该预测方法的有效性，试制了3种断面结构不一致的轮胎并分别进行耐久性实验与Df预测，从结果确认了预测Df与耐久实验结果之间的规律，证明可将这种方法应用于胎圈Nf的预测，最后对利用ΔSED计算轮胎Df时预测值偏低的情况进行了分析。