基于Hopkinson 压杆的M 型试样动态拉伸实验方法研究*

2020-08-26 06:40董新龙俞鑫炉

爆炸与冲击 2020年8期

舒旗，董新龙，俞鑫炉

（1. 宁波大学冲击与安全工程教育部重点实验室，浙江宁波 315211；2. 北京理工大学机电学院，北京 100081）

在设计和分析冲击载荷作用的工程结构时，需通过实验获取材料可靠的动态力学性能，来发展或校核材料的本构模型。分离式霍普金森压杆（split Hopkinson pressure bar, SHPB）动态实验技术加载简单、测试精度高，已广泛用于高应变率下材料动态压缩性能研究[1-5]，而高应变率下的动态拉伸、扭转性能的测试，目前仍相对困难[6]。近几十年，已发展了多种形式Hopkinson 拉杆实验装置，其中最被关注的问题就是试样与入射杆和透射杆的连接对测试结果的影响[7-13]。目前，在Hopkinson 拉杆实验装置中，主要采用粘接、螺纹或销钉等方式，将入射杆、透射杆与试样轴肩连接。由于连接强度低[8-10]，这些粘接方式无法满足较高强度材料的性能测试需要；而螺栓及销钉连接必须有极高的加工和安装精度，以保证测试结果的可靠性。Nicholas[7]探讨了连接对测试结果的影响，并指出：对带连接螺纹的试样，要得到可靠的高应变率拉伸实验结果，必须保证试样与拉杆螺纹孔间无任何间隙的精密配合，并保证拉伸试样与杆完全水平对齐；连接螺纹间隙或试样与杆端接触不紧密，将会产生反射应力波，并被来回传播放大，导致实验结果的极大误差，难以获得准确可靠的拉伸材料性能结果。目前，Hopkinson 拉杆常采用的连接方式是，将带有螺纹肩部的拉伸试样直接拧入杆两端的螺纹孔中。在拉伸波作用下，试样的螺纹肩部、头部与杆端必定分离，出现自由面，而应力波在自由面的反射，会导致实验误差。而且，粘接是通过有机胶黏剂将试样粘结在入射杆和透射杆之间，这样虽可以避免螺纹或销钉连接中存在的间隙干扰，但因有机胶黏层具用较大黏弹性，拉伸时黏胶层产生的大变形对采用一维应力波理论计算的试样应变有较大影响[13]，并且胶粘固化时间长、实验效率低。

对于Hopkinson 拉伸杆实验技术存在的问题，Mohr 等[14]曾提出采用Hopkinson 压杆对M 型试样加载，M 型试样可将压缩应力波转为对试样的动态拉伸加载，这样可以避免试样与杆的连接问题。但该方法提出后，未见采用和实验验证。一方面，可能是M 型试样加工相对困难，另一方面，动态拉伸工程应用需求较多的是薄板材料（如汽车钢板），不适合制作M 型拉伸试样。近年来，增材制造的应用领域不断发展，3D 打印金属材料的动态拉伸性能及破坏特性研究也被关注[15-17]，有必要发展小试样的动态单轴拉伸实验方法。为此，本文中，对M 型试样动态拉伸实验开展实验和有限元数值分析，分析M 型试样的设计，探讨试样Hopkinson 动态实验的一维应力和均匀性假设、实验数据处理方法、加载波形、M 型试样弹性修正等对实验结果的影响，并进一步开展准静态及动态实验验证。以期为M 型动态拉伸试样的设计、分析和应用提供参考。

1 M 型试样拉伸实验和分析

1.1 M 型试样拉伸原理

M 型试样的拉伸及加载原理如图1（a）所示，该方法最大特点是，将在试样两端施加的压缩载荷转换为对DE、D1E1两段的拉伸加载。实验中，可通过对DE、D1E1拉伸标段的受力、变形分析，获得材料的拉伸性能。该方法既可用于准静态拉伸试验，同时也可以方便地通过Hopkinson 压杆加载开展材料动态拉伸实验，如图1（b）所示。该方法实验安装便捷，不需要试件与Hopkinson 拉杆间的连接，避免了连接间隙引起的反射应力波给实验带来的误差。Mohr 等[14]为保证试样整体刚度，设计试件厚度较大，拉伸标段DE、D1E1与试样整体厚度相同，拉伸段为宽度远大于厚度的薄板形，可按一维应变拉伸状态处理。

图1 M 型试样的拉伸加载原理Fig.1 Schematic of quasi-static and dynamic tensile test for M-specimen

1.2 试样设计和变形分析

由于M 型试样拉伸标段DE、D1E1仅为结构的一部分，有必要对试样在压缩载荷作用过程中力的传递、各部分的变形状态和对实验结果的影响进行分析，合理设计M 型试样以保证拉伸标段DE、D1E1的均匀拉伸变形。

1.2.1 刚度分析

理论上，M 型拉伸试样整体结构（见图1（a））中，ABC、ABC1、EFG、E1F1G1和CBC1部分应有足够的刚度，保证加载过程这些部分压缩和转动变形尽量小，避免对试样拉伸段DE、D1E1的变形产生影响。由于Hopkinson 压杆尺寸受限制，试样的整体尺寸和刚度是有限的。在压缩过程中，各部分变形量不同，会导致试样的FG 段绕E 点发生转动，图2（a）为M 型试样加载有限元模拟结果。由图2（a）可见：由于试样发生畸变，G 和G1点向外运动，形成外八字形状，对DE 拉伸标段有附加弯矩作用，影响拉伸结果。因此，在试样结构和尺寸设计时，应考虑尽可能减小畸变影响。为此，采用封闭M 型试样设计，并减小AB 和ED 段间的间隙Δ，如图2（b）所示，以增加试样整体的刚度，减小畸变影响。

针对直径14.5 mm 的Hopkinson 压杆，设计试样尺寸（见图2（b））分别为：a=4.4 mm，b=14 mm，c=14 mm，d=12 mm，e=7.2 mm，间隙Δ=0.1 mm，试样的整体厚度h=3.5 mm。试样拉伸标段尺寸为：长l0=2.2 mm，截面为1 mm（厚度t）×1.5 mm（宽度w）的矩形。

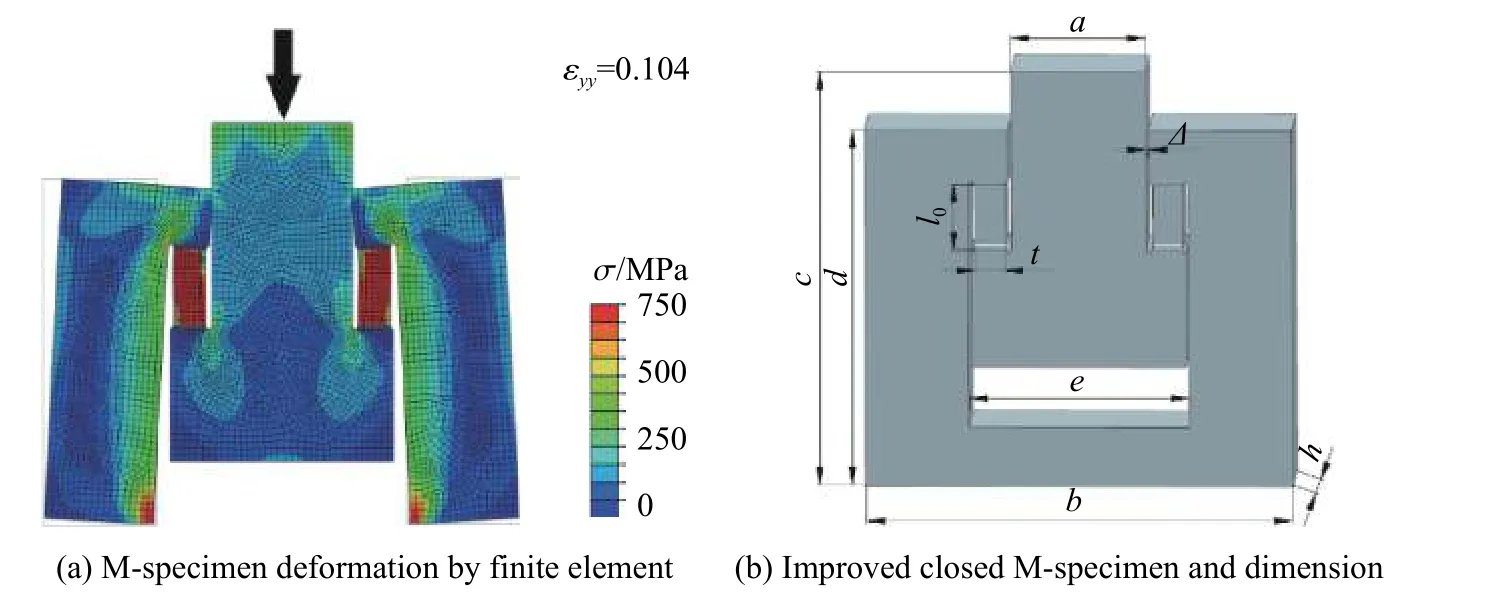
图2 M 型试样变形和改进Fig.2 M-shaped specimen deformation and improvement

1.2.2 拉伸应力应变分析

无论是M 型试样的准静态实验还是Hopkinson 动态实验，一般只能测得试样两端的压缩载荷 F (t) 和总位移 U (t) ，而M 型试样拉伸标段只是其中一部分。因此，试样两端测得的位移U 包含试样拉伸标段的变形和试样其他部分的弹性变形贡献。为了获得试样拉伸标段的变形位移，设试样拉伸标段ED 塑性变形引起的位移为 Up(t) ，而试样弹性变形部分引起的位移为 Ue(t) ，则有：

假设 Ue(t) 与试样的整体刚度相关，并与施加的载荷力成正比：

则拉伸标段的工程塑性应变可表示为：

式中：K 为试样刚度系数， F (t) 为试样两端的压缩力， l0为拉伸标段的初始长度。

拉伸标段的工程应力可表示为：

式中：A=2wt 为拉伸标段的横截面积。则相应的真应力、真应变分别为：

实验中，只要测试M 型试样两端的载荷 F (t) 和位移 U (t) ，确定试样刚度系数K，就可分析得到材料拉伸标段的应力应变曲线。

1.2.3 Hopkinson 动态加载分析

基于Hopkinson 压杆的M 型试样动态拉伸实验加载测试原理如图1（b）所示，M 型试样位于入射杆与透射杆之间。

假设在加载过程中所设计的M 型拉伸试样满足Hopkinson 杆实验的一维应力条件，即εi(t)+εr(t)=εt(t) ，则根据一维应力波理论，可方便得到M 型试样x1、x2两端的动态载荷 F (t) 、速度差 dv(t)和位移 U (t) :

式中： εi(t) 、 εr(t) 、 εt(t) 分别为入射波、反射波和透射波的应变，Ab为压杆的横截面积， c0为压杆的弹性波速，E 为压杆的弹性模量； vx1(t) 、 vx2(t) 分别为试样与入射杆的速度、透射杆接触面x1、x2处的速度。

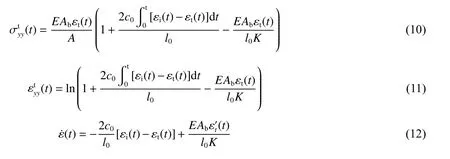
2 动态有限元分析

为了探讨在Hopkinson 压杆实验加载过程中所设计M 型试样的一维应力和试样均匀性条件，分析动态数据处理方法的可靠性，采用有限元方法，对在Hopkinson 压杆加载下的封闭M 型试样波传播特性和变形特征开展数值分析。

2.1 有限元模型

采用Abaqus/Explicit 有限元程序，对分离式Hopkinson 压杆作用下M 型试样动态拉伸实验进行建模和分析。试样采用C3D8R 四面体实体单元，共有20 760 个单元，其中拉伸标段8 800 个单元，最小单元尺寸为0.01 mm。试样拉伸段截面较小，采用铝合金杆，以提高透射波信号。入射杆和透射杆直径为14.5 mm、长1 000 mm，采用C3D10M 实体单元，入射杆33 641 个单元，透射杆20 184 个单元，最小单元尺寸为0.04 mm。

为了便于比较不同加载波形、不同加载率下应力波在试样中传播的特征，不考虑金属试样本构应变率效应，采用简单的指数硬化弹塑性模型： σ =A+Bεn。其中，A、B、n 分别为材料的屈服强度、应变强化系数、应变硬化指数，取A=620 MPa、B=200 MPa、n=0.3，弹性模量Es=210 GPa。铝合金压杆采用线弹性本构：Eb=71.1 GPa，ν=0.35， = 2.70 kg/m3。

2.2 有限元结果和分析

有限元模拟中，采用了不同撞击杆速度撞击入射杆，考察不同加载率、不同加载波形下M 型试样的动态响应特征和Hopkinson 实验基本假设的满足情况。

2.2.1 改进后试样的变形特征

在300 mm 撞击杆以速度v=2.38 m/s 冲击下，M 型试样与透射杆接触端的作用力、试样两端压缩位移和试样整体变形特征，如图3 所示。由图3 可见：动态加载过程中，试样压缩位移稳定增大；当t=95 μs时，试样两端位移U=0.241 mm、拉伸标段轴向应变达到εyy=0.104，试样整体仍保持均匀、稳定变形状态，没有发生明显的畸变，与原开口M 型试样变形状态相比（见图2（a）），试样整体的弯曲畸变得到明显改善。可见，在保持结构基本尺寸不变的情况下，改进封闭的M 型试样设计，试样整体刚度得到显著提高，试样畸变的影响明显减小。

图3 M 型试样的加载力、压缩位移和整体变形Fig.3 Dynamic force, compression displacement and global deformation of M-specimen

再对试样拉伸标段的应力分布均匀性进行分析，图4 为封闭M 型试样拉伸标段的应力演化和不同位置的等效应力曲线。由图4 可见：在加载前期（t＜27 μs，压缩位移小于15 μm），试样拉伸标段仍存在畸变引起的弯矩作用，但随着拉伸变形的发展，在试样整体压缩位移至35 μm 后，沿试样拉伸标段不同位置的等效应力趋于均匀，畸变引起的弯矩减小。因此，试样拉伸标段的变形可看作一维应力拉伸状态。

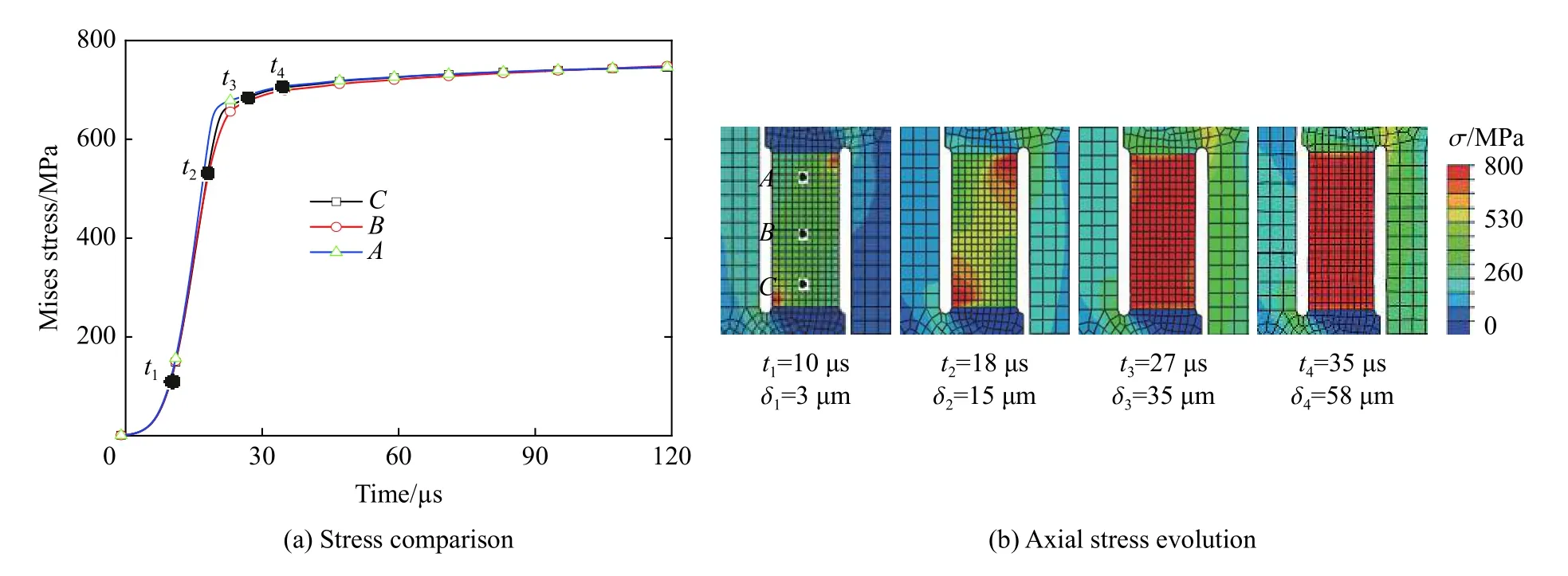
图4 拉伸标段不同位置点的应力比较和轴向应力演化Fig.4 Stress comparison and axial stress evolution at different points of tensile section

2.2.2 Hopkinson 实验基本假设满足情况

Hopkinson 压杆动态实验分析要求试样设计必须满足一维应力假设，即 εi(t)+εr(t)=εt(t) 。用有限元模拟了撞击杆速度v0分别为2.38、3.50、4.50 和6.80 m/s 状况下，M 型试样在不同加载速度下的响应特性和试样两端动态力的平衡状态。

当撞击杆速度v0=2.38 m/s 时，入射杆和透射杆上的入射波 εi(t) 、反射波 εr(t) 和透射波 εt(t) ，如图5（a）所示。按Hopkinson 一维应力假设，由式（7）可得试样两端的加载力曲线，如图5（b）所示，可见两者符合较好。不同速度的有限元结果均有类似的结果，表明所设计的M 型试样均能较好满足Hopkinson 压杆实验的一维应力假设，可以按式（7）分析M 型试样的动态拉伸力。

图5 典型的入射波、反射波和透射波Fig.5 Typical incident, reflected and transmitted wave

图5（b）中，M 型试样两端动态力均存在震荡现象。不同速度下的模拟结果如图6 所示，可见，随着冲击速度的增大，试样载荷震荡也增大，并且震荡周期近似相同，约15.78 μs。这是由于，M 型试样结构中存在多个自由表面（如图1 中CBC1和EF），应力波在试样中按A→B→C→D→E→F→G 顺序传播，过程中将在自由面发生反射、透射。从A 到E 距离为20.85 mm，按试样材料弹性波速5 170 m/s 计算，来回反射传播时间约为8.2 μs，与震荡半周期近似相同。该震荡周期是应力波在自由面反射、透射引起，而其本身具有短历时上升，弥散震荡的矩形应力加载波经试样自由面反射、透射会被放大，加剧波形的震荡，这将影响实验拉伸应力分析。

为了减小动态力的震荡对实验分析的影响，在入射杆端加贴紫铜片，调整为三角波形加载。图7 为

图6 不同速度下载荷的震荡Fig.6 Loading oscillation at different velocities

图7 三角波加载下的入射波、反射波和透射波Fig.7 Incident, reflected and transmitted wave by pulse shaper

三角波形加载的典型入射波、反射波和透射波，还给出了与 εi(t)+εr(t) 的比较。由图7 可见，与矩形波加载相比，试样两端力的震荡明显减小，同时试样两端准静态平衡假设也更好符合。因此，在高应变率下M 型试样的Hopkinson 实验中，建议采用波形整形器方式加载，有利于改善应力平衡、减小试样结构的影响。

2.2.3 拉伸应变分析和弹性修正

采用波形整形器加载时，有限元模拟的典型M 型试样动态载荷 F (t) 和试样两端的总位移U (t) ，如图8 所示。作为比较，图8 中还有试样拉伸标段两端的实际位移Ul(t) 和通过入射波 εi(t) 、反射波 εr(t) 和透射波 εt(t) 按式（9）得到的试样两端总位移Ub(t) 。由图8 可见：Ub(t) 与试样实际位移 U (t) 很好符合，表明采用Hopkinson 一维应力分析可以准确得到M 型试样两端的位移；而试样两端位移 U (t) 大于Ul(t) ，正如上节分析，M 型试样结构的弹性变形影响不能忽略，在计算拉伸标段应变时，需对 U (t) 进行修正，消除位移 U (t) 中由M 型试样结构弹性变形引起的部分。

M 型试样载荷F(t)-位移U(t)曲线如图9 所示，弹性段斜率K 为M 型试样的刚度系数，K=49.101 kN/mm。根据式（1）～（2），可计算试样拉伸标段的塑形变形位移： Up(t)=U(t)-F(t)/K ，相应的 F (t) -Up(t) 曲线如图9 所示。为了校验拉伸塑性变形位移Up(t)的可靠性，图9 还给出了有限元模拟的试样拉伸标段两端的实际位移Ul(t) ，位移Ul(t) 包含弹性和塑性变形两部分的贡献。因试样拉伸标段为单轴拉伸变形，塑性变形产生的位移 Ups(t) 为：

式中： F (t)l0/(EsAs) 为标段弹性变形部分。相应的 F (t) - Ups(t) 曲线如图9 所示，可见 F (t) - Ups(t) 曲线与 F (t) -Up(t) 曲线符合，说明对试样整体位移 U (t) 弹性修正后，可以得到精确的试样拉伸标段塑性位移Up(t) ，这验证了修正方法的可行性。因此，在M 型试样Hopkinson 动态拉伸实验中，可以通过入射波、反射波和透射波，直接采用式（10）～（12），得到M 型试样拉伸标段的应力、塑性应变和应变率。

图8 动态载荷、位移和标段位移Fig.8 Dynamic force, global and local displacement

图9 力-位移曲线及修正Fig.9 Amendment of force-displacement curve

图10 为不同撞击速度下有限元计算的一组动态真应力应变曲线，图10 还给出了试样拉伸标段中点的等效应力应变曲线和相应材料的本构方程曲线，三者符合较好。这表明，基于Hopkinson 压杆的M 型试样动态拉伸实验的应力-塑性应变曲线能较好地反映材料的动态拉伸性能。图11 为不同冲击速度（1.7～6.8 m/s）下有限元模拟的一组应力应变曲线。由图11 可见，加载应变率可达4 700 s-1甚至更高，因此，基于Hopkinson 压杆的M 型试样拉伸实验可实现高应变率的动态拉伸测试。

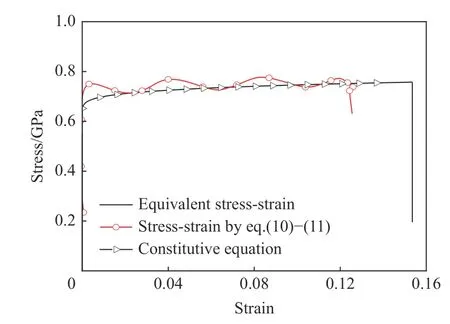
图10 实验模拟应力应变曲线和本构方程Fig.10 Stress-strain curves and constitutive equation

3 M 型试样Hopkinson 动态实验验证

图11 不同应变率下的真应力应变曲线Fig.11 True stress-strain curves under different strain rates

3.1 试样和实验测试

3.1.1 试样制备

M 型拉伸试样由德国Eos M280 型金属粉末3D 打印机制备。采用颗粒度为35 μm 的GP1 不锈钢粉制作，其化学成分分别为：w(Fe)= 74.54%，w(Mn)=0.61%，w(Cu)=2.69%，w(Si)=0.63%，w(C)=0.05%，w(Cr)=17.54%，w(Ni)=4.36%。制备过程中，采用氮气保护，防止氧化[18]。一次整版打印46 个M 试样，以保证制备的试样性能一致。

3.1.2 实验和测试

对GP1 不锈钢M 型试样开展准静态和Hopkinson 动态拉伸实验。为了验证实验数据分析方法的可靠性，试样表面喷涂散斑，采用FASTCAM APX RS 超高速相机（采样频率106s-1）记录实验动态变形，采用二维图像相关法（DIC）分析可直接得到试样拉伸标段的位移、应变，用于与实验数据分析得到的结果比较、验证。

准静态M 型试样拉伸实验在MTS-810 型材料试验机上完成，采用位移控制，速度为0.04 mm/s。动态M 型试样拉伸实验在直径14.5 mm 的Hopkinson 压杆上进行，考虑拉伸透射波信号较小，在实验中采用铝合金压杆，子弹长度300 mm，在入射杆端加贴厚0.5 mm 紫铜片波形整形器。

3.2 实验结果和分析

3.2.1 准静态实验结果

图12 为准静态实验测到的载荷 F (t) 和试样两端压缩位移 U (t) ，其中，U (t) 采用DIC 分析得到。作为比较，图12 还给出了DIC 分析得到的试样拉伸标段的位移Ul(t) 。与理论、有限元分析结果相同，实验测得的试样两端位移 U (t) 大于拉伸标段局部位移Ul(t) 。为了获得精确的拉伸标段应变，必须进行弹性修正。需要说明的是，在变形较大时，由于试样表面喷涂散斑会脱落破坏，DIC 分析无法得到加载过程完整的变形 U(t)和标段拉伸位移Ul(t) 。

图12 载荷和位移曲线Fig.12 Load and displacement curves

图13 为实验测到的试样两端的载荷 F (t) -位移 U (t) 曲线，该曲线弹性段的斜率K 即为实验试样的刚度系数（K=40.6 kN/mm），结果与有限元数值模拟的刚度系数（K=49.1 kN/mm）基本一致。按式（2）对U(t)弹性修正得到拉伸标段塑性位移 Up(t) ，再按式（5）～（6）计算试样的真应力-塑性应变曲线。图14 为弹性修正前和修正后的材料准静态真应力应变曲线。作为验证比较，图14 还给出了采用DIC 分析直接得到的试样拉伸标段中点的轴向应力-塑性应变曲线，可见对位移 U (t) 修正后，按式（5）～（6）得到的应力应变曲线与DIC 分析直接测得的应力应变曲线符合很好。这表明，改进封闭M 型试样设计后，拉伸标段很好满足单轴拉伸状态，所采用的位移修正处理方法可消除试样结构弹性变形的影响，满足材料单轴拉伸性能实验测试要求。