关注问题本质 归纳解决方法

文／高 健

等可能条件下的概率问题是中考中的热点问题，这类问题的背景材料越来越贴近我们的生活，难度适中。接下来，我们将对两类典型问题进行分析，根据题目的特点归纳出合适的解决策略与方法。

类型一 用面积法求概率

例1 一个小球在如图1 所示的方格地砖上任意滚动，并随机停留在某块地砖上，每块地砖的大小、质地完全相同，那么该小球停留在阴影部分的概率是______。

图1

例2 如图2，在正方形ABCD内任取一点O，连接OA、OB，得到△ABO，如果正方形ABCD内每一个点被取到的可能性相同，则△ABO是钝角三角形的概率是_____。

图2

【分析】本题同样考查的是几何图形中的概率问题。我们首先要想到当点O在以AB为直径的半圆上时（如图3），△ABO为直角三角形。因此，当点O在半圆中时（如图4，阴影部分不包含边界），△ABO为钝角三角形。

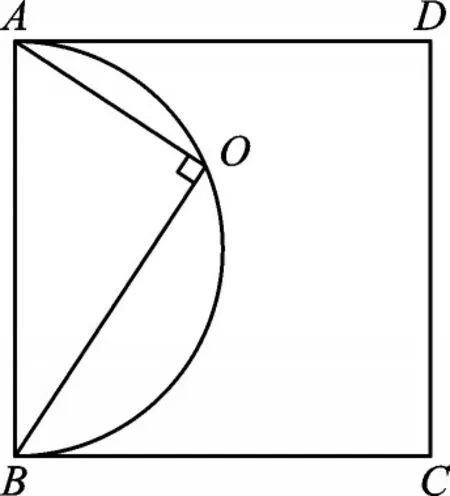
图3

图4

类型二 用列举法求概率

常用的列举法有列表法和画树状图法，这也是中考中概率问题的考查重点。同学们需要掌握技巧，做到触类旁通。

例3 一张圆桌旁设有4 个座位，丙先坐在了如图5 所示的座位上，甲、乙2 人等可能地坐到①、②、③中的2个座位上。

（1）甲坐在①号座位的概率是______；

（2）用画树状图或列表的方法，求甲与乙相邻而坐的概率。

图5

【分析】（1）由题意可判断出该事件是等可能事件，直接根据概率公式计算即可。（2）由题意可判断出本题属于“不放回”问题，相当于一个口袋里有红球、白球和绿球各1个，不放回地随机取两次。

（2）画树状图如下：

∴共有6 种等可能的结果，其中甲与乙恰好相邻而坐的结果有4种，

【分析】由题意可判断出本题属于“有放回”问题，相当于一个口袋里有红球和绿球各1个，有放回地随机取三次。

解：画树状图如下：

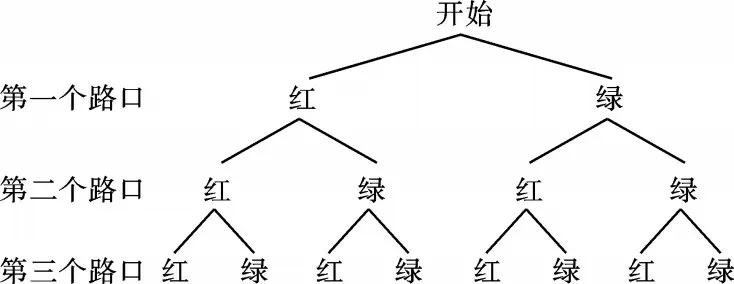
∵经过三个路口共有8 种等可能的结果，其中恰有一次遇到红灯的结果有3种，