电压模式Buck电路中Type III型环路补偿优化方法
洪怡雯,陈伯文,2,王 强,汤苏雷
(1.苏州大学电子信息学院,江苏苏州 215006;2.苏州路之遥科技股份有限公司,江苏苏州 215153;3.苏州大学应用技术学院,江苏苏州 215325;4.华硕科技苏州有限公司,江苏苏州 215011)
电子设备电源市场需求越来越大,各种专用芯片和微处理器的大量应用对电源的性能要求变得愈加严格。电压模式Buck 电路由于只存在单一电压环路补偿反馈设计,相比电流模式调试更加容易、脉冲宽度调制(PWM)三角波的幅值大,脉冲宽度调节时具有较好的抗噪声性能、对输出负载的变化有较快的响应速度、低输出阻抗等特点,使得应用领域愈加广泛,与此同时,专用芯片和微处理器工作所需电压不断降低,负载电流和电源工作频率直线上升,对电压模式Buck 电路电压输出也提出了越来越高的要求[1-3]。
电压模式Buck 电路在输出低电压负载大电流情况下具有高稳定性和可靠性。本文提出了基于Type III 型环路补偿中零极点理论的优化方法,与无补偿时电压模式Buck 电路及传统电压模式Buck 电路的Type III 型环路补偿方法相比,所提优化方法改善了电路系统的相位裕度,保证了Q点附近幅相特性曲线的稳定性,更好地实现了零极点抵消,扩展带宽,减小输出电压振铃周期,降低输出电压的超调和下冲,从而减小输出电压动态响应误差和加快动态响应速度。
1 电压模式Buck 电路系统与理论分析
1.1 电压模式Buck 电路整体系统
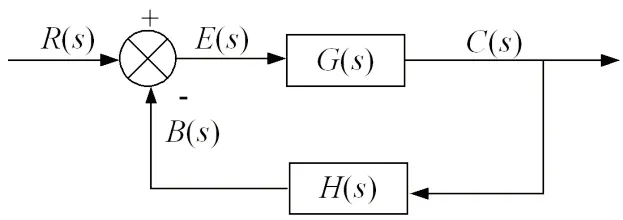
图1 为电压模式Buck 电路整体系统框图,由输入模块、滤波储能模块、控制开关模块、反馈输出模块、环路补偿模块组成。该电路系统采用同步整流技术,相比肖特基二极管开关电路有更高的功率转换效率、更低的电路调压损耗、更快的响应速度,非常适合低输出电压、高输出负载电流、小体积的电子设备,利用PWM 控制MOS 管上管(HMOS)和下管(LMOS)导通截止,通过输出电压分压反馈来调整PWM 的占空比,从而确定输出电压的大小、输出电感和输出电容进行能量存储释放和滤波,通过Type III 环路补偿实现电路在稳态负载及动态负载下输出电压的稳定性[4]。
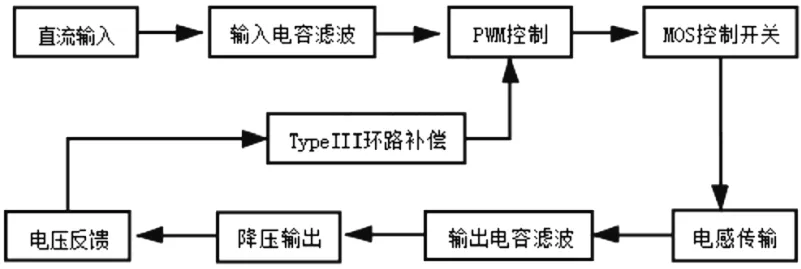
图1 电压模式Buck 电路整体系统框图
1.2 电压模式Buck 电路调节原理分析
电路采用UP1542 为电源转换芯片,设计的电压调节回路如图2 所示,当该电压调节回路不含ZFB和ZOUT组成的环路补偿模块时,由输入电压Vin、PWM 电源转换芯片UP1542、HMOS、LMOS、电感L、输出电容C、输出电压Vout组成的基本同步整流Buck 型开关电路外,控制环仅有一个电压反馈环,电压反馈环包括跨导型电压误差放大器(Error Amplifier)、反馈分压电阻R1、R2和PWM 比较器(PWM Comparator)。
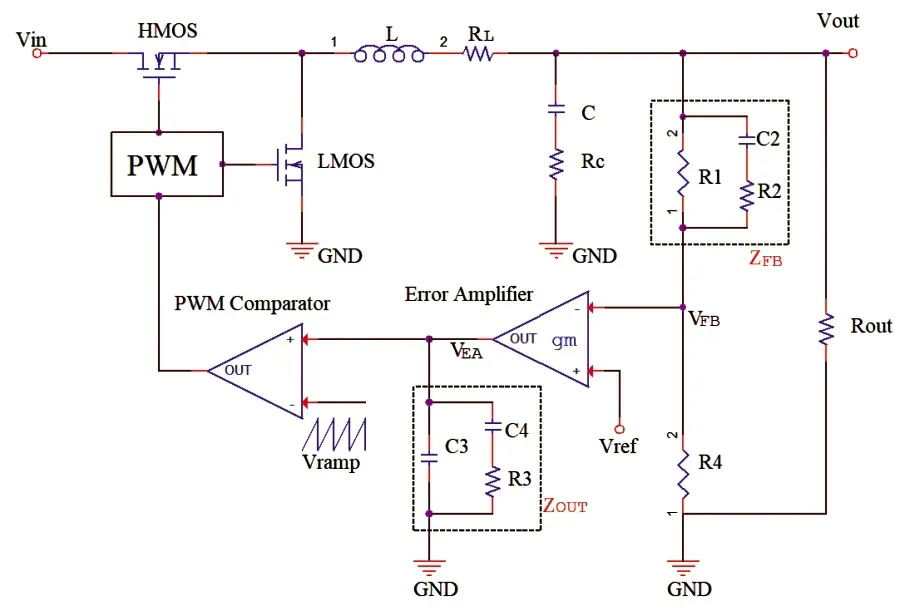
图2 UP1542电压调节回路
输出电压通过分压得到反馈电压VFB,该电压通过电压误差放大器检测到输出电压的微小变化,变换差值被电压误差放大器放大输出,输出电压VEA得到一定幅值的噪声较小的直流反馈电压信号,反馈的电压信号VEA与电源芯片内部产生的斜坡电压Vramp通过PWM 比较器比较产生高低信号控制PWM 的占空比,PWM 信号控制HMOS 和LMOS 导通和截止来控制输出稳态电压的精度[5-7]。
1.3 功率级传递函数
由图2 可知,当该电压调节回路不含ZFB(由C2、R2构成)和ZOUT(由R3、C3、C4构成)组成的环路补偿模块时,芯片的功率级传递函数为:
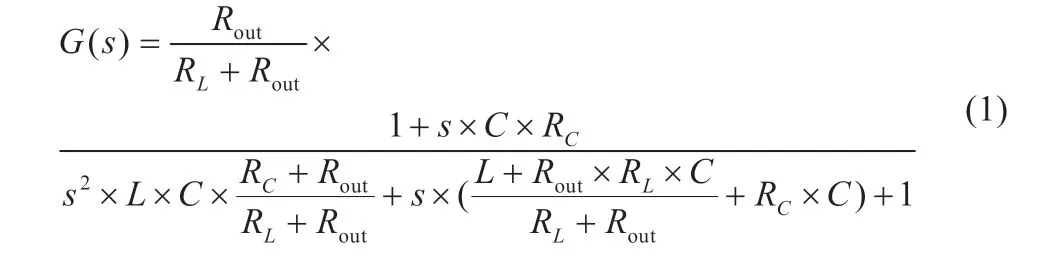
由于电感寄生电阻RL和电容等效串联电阻RC相对于负载电阻Rout可以忽略不计,式(1)可化简为:
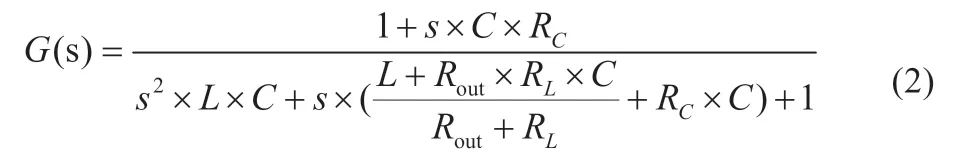
由式(2)可知,系统传递函数存在2 个极点和1 个零点,输出电容C与L会在谐振频率点处引入一个双极点,谐振点的频率为:

输出电容的等效串联电阻RC与输出电容C会在fesr引入一个零点:

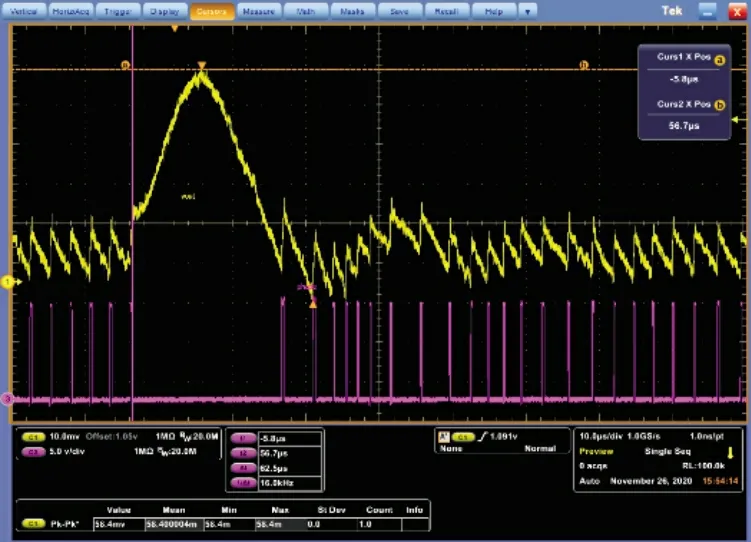
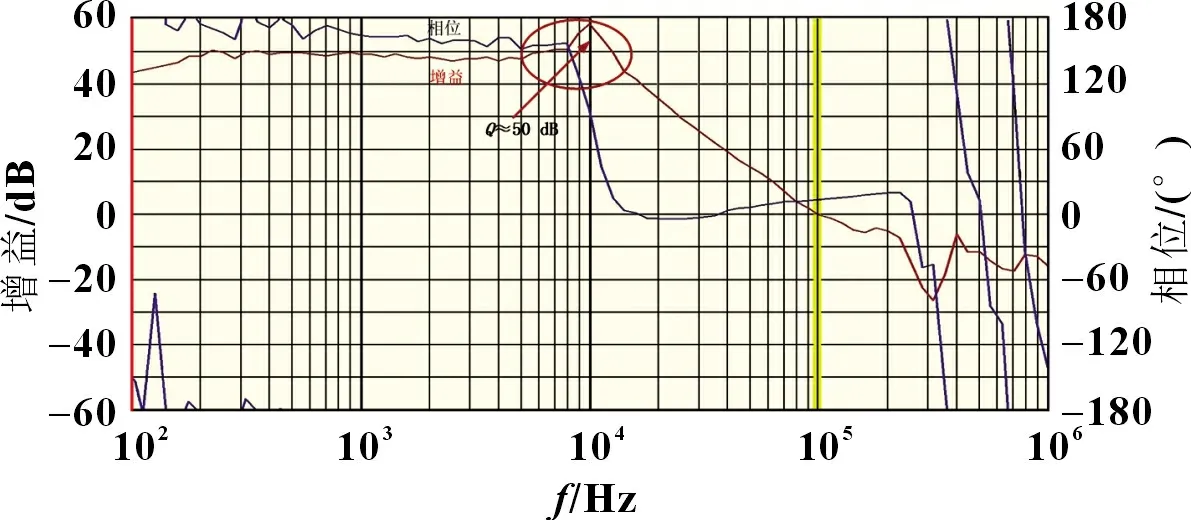
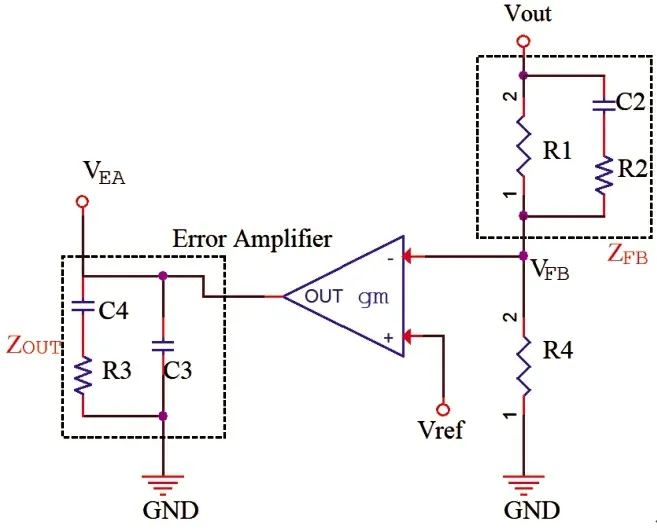
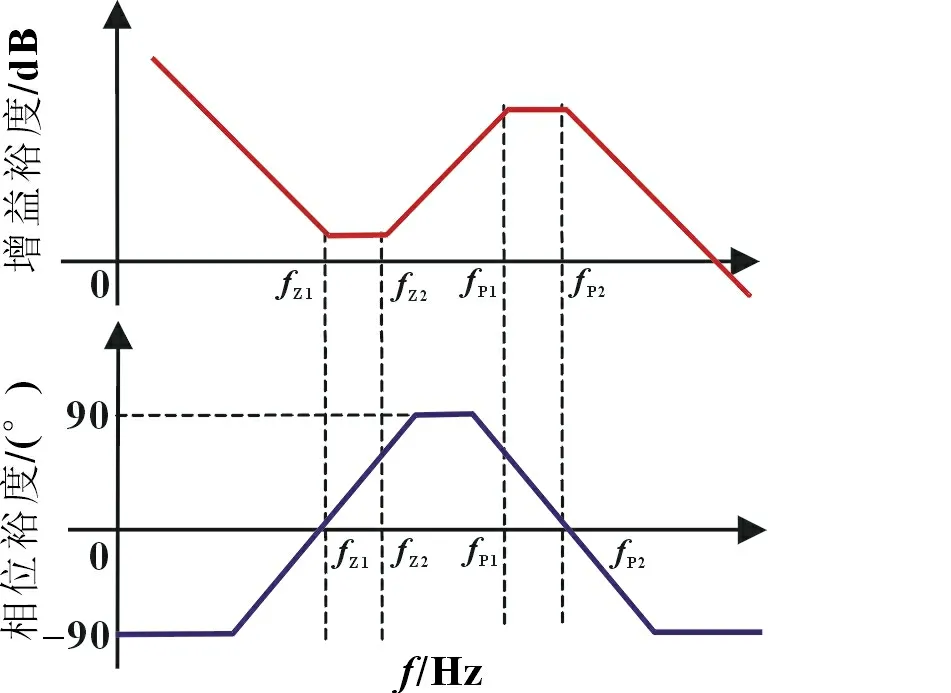
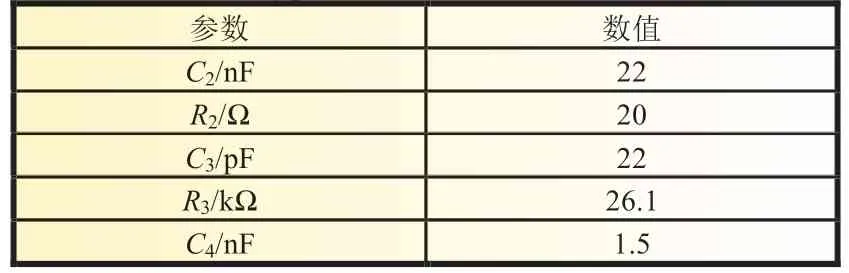
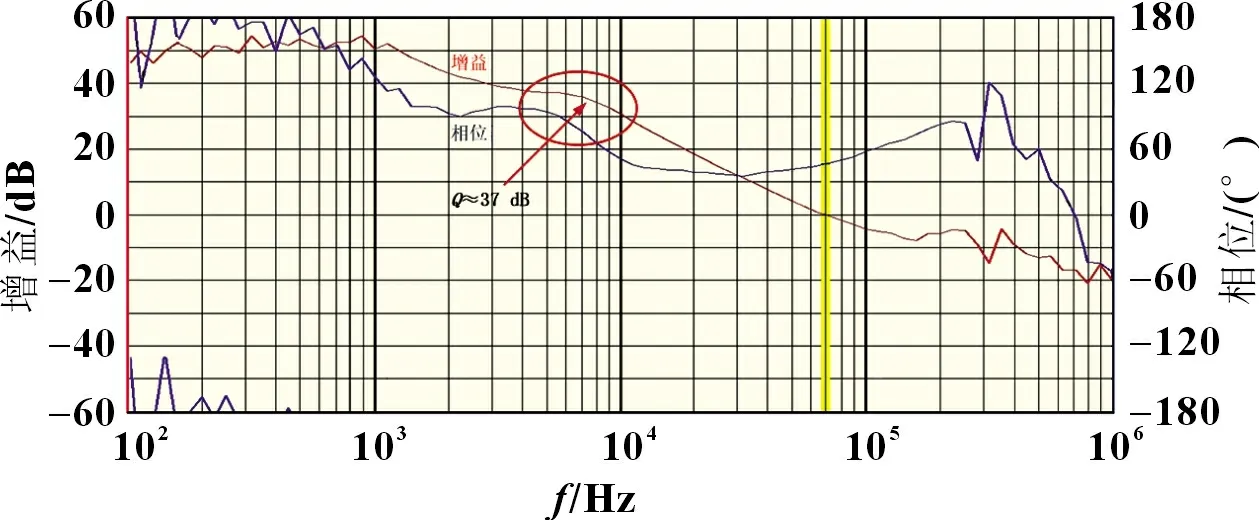
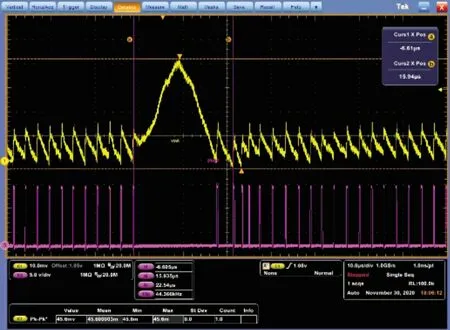
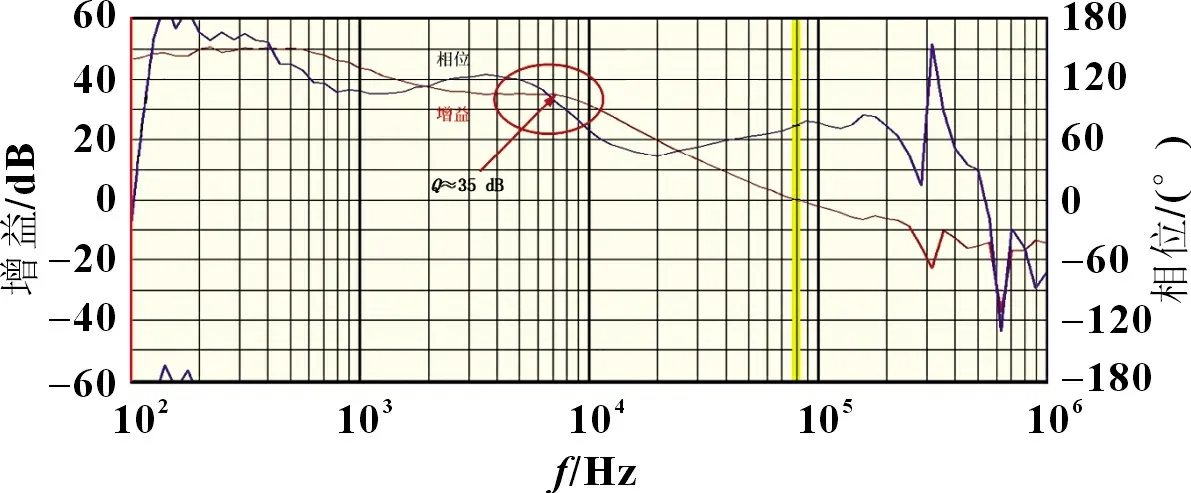
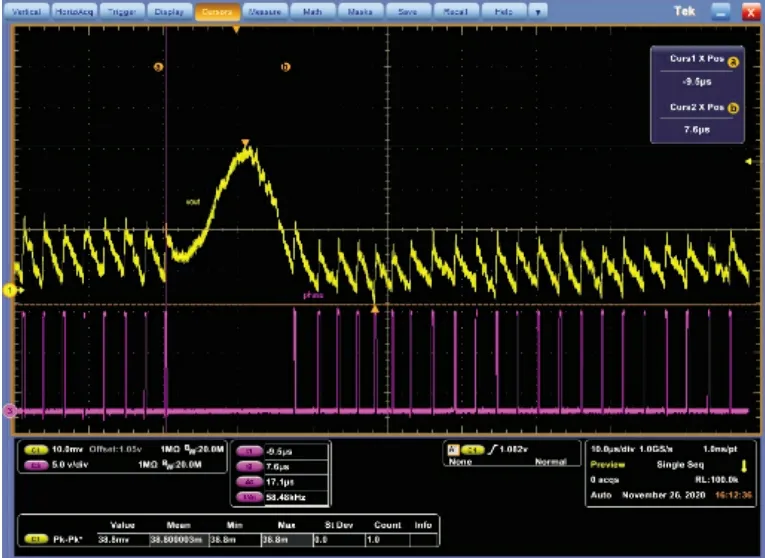
由LC 网络及其寄生参数构成的品质因素Q的表达式如式(5)所示。通常情况下fLC< 以UP1542 输入12 V、输出1.05 V、开关频率300 kHz、截止频率f0为70 kHz,输出动态响应误差低于5%的设计为例,环路无补偿时,其设计参数如表1 所示。其幅频特性曲线如图3 所示,其电路系统输出电压的瞬态响应如图4 所示,在电压模式Buck 电路无环路补偿时,其截止频率f0为98.52 kHz,增益裕度为0 dB 时的增益斜率为-45.6 dB/dec,得到的相位裕度为13.24°,品质因素Q为50 dB,且在Q点后,相频特性曲线发生突变,使系统的稳定性受到影响,电压的瞬态响应超调为58.4 mV,通过观察图4 示波器3 通道PWM 点的脉冲调整频率,得到电压动态响应时间为62.5 μs。 图4 无环路补偿下输出电压动态响应 表1 电压模式Buck 线路设计参数 图3 环路无补偿时幅相特性曲线 由图4 可知,输出的高频噪声频率较高且幅值超过了输出动态响应误差的要求,因此需要对动态响应误差进行恰当衰减,如果输出动态响应高频噪声衰减不充分,系统容易受到干扰,如果输出动态响应高频噪声衰减过大,系统的带宽变窄,动态响应速度则会较慢,因此需要设计由ZFB、ZOUT组成合适的Type III 型环路补偿网络,使电压误差放大器在低频时增益高,在高频时增益低,使得电路闭环系统稳定工作。 如图2 所示,在输出电容后,加入ZFB和ZOUT模块来连接误差放大器,组成Type III 型环路补偿网络来优化输出电压,使电路形成一个优化的动态响应闭环控制系统。开环控制系统的电源电路不能检测输出电压误差,也不能校正误差,控制输出电压的精度、抗电路干扰能力及动态响应的性能都比较差,仅适用于精度不高的场合。Type III 型环路补偿网络与Buck 电路形成闭环控制系统,通过为环路提供补偿零极点,改善环路的相位裕度,以保证环路稳定,同时实现零极点的抵消来扩展电路系统带宽,加快系统的响应速度。环路补偿网络充分发挥了反馈的重要作用,当输出电压动态变化时,通过该补偿反馈到PWM 斩波,快速调整PWM 斩波的占空比来消除电压变化所产生的偏差,保证输出电压的稳定性[8]。 图5 为Buck 电路整体闭环模型。已知Buck 电路传递函数G(s)(从控制到输出)和跨导Type III 型环路补偿传递函数H(s),因此整体电路闭环传递函数在S域H'(s)的基本方程为: 图5 Buck电路整体闭环模型 当满足式(7)时,电路工作稳定,θ 为环路传递函数的相角裕度。当G(s)H(s)=-1 时,增益裕度为0 dB,相角裕度为180°时工作频率为截止频率f0,闭环传递函数值将无穷大。截止频率f0大小会给电路稳定性带来影响,由奈奎斯特采样定理可知:电力电子变换器输出电压的截止频率f0理论上最高是开关频率的一半。 为了使开关电源系统稳定且具有较好的稳态和动态性能,在环路补偿中,应使补偿后的系统开环传递函数符合以下四点:系统的相位裕度为45°~75°,相位裕度过大响应较慢,过小则系统容易不稳定;开环传递函数以-20 dB/dec 的斜率穿越0 dB 线,并且覆盖足够的频带宽度,保证系统的稳定性;开环传递函数的静态增益决定输出值与给定值的稳态误差,增益高则系统的稳态精度高;兼顾系统的快速性及开关频率的限制,截止频率f0低于电源开关频率的1/5~1/2。 结合UP1542 提供的内部电路逻辑,如图6 所示,H(s)模块为跨导运算放大器Type III 型环路补偿网络模型在S域的表达函数,gm为运算放大器的跨导。其S域反馈传递函数为: 图6 跨导运算放大器Type III型补偿网络模型 式中:ZFB(s)和ZOUT(s)为ZFB和ZOUT模块在S域的模型。 化简可得: 由此得到该环路补偿网络的反馈传递函数提供了三个极点和两个零点。图7 为Type III 环路补偿波特图,极点使相位产生-90°的相移,使增益曲线斜率向下转折20 dB/dec;零点使相位产生90°的相移,使增益曲线斜率向上转折20 dB/dec,因此零极点的位置对系统的稳定性起着重要作用,如式(10)所示: 图7 Type III环路补偿波特图 由H(s)求解出的极点fP1应设置在输出电容的等效串联电阻RC和输出电容C共同产生的零点处,用来抵消该零点对电路的影响,增强电源的抗干扰能力,极点fP2放置在电路开关频率的一半处,为电路提供一个极点,降低构成的控制环路对电源高频噪声的敏感度,使增益曲线斜率向下转折-20 dB/dec。 由H(s)求解出的零点fZ1和fZ2如式(11) 所示,设置在G(s)模块输出电感输出电容的谐振点fLC附近。由于在接近谐振频率的区域内发生相移突变,使线路非常不稳定,零点fZ1和fZ2能够很好地抵消这一影响。 结合表1 的电压模式Buck 电路基本参数,增加Type III 环路补偿理论设计参数如表2 所示,其幅频特性曲线如图8 所示,其输出电压的动态响应如图9 所示,当开关电源环路补偿参数值为理论设计值时,其截止频率f0为68.51 kHz,增益裕度为0 dB 时的增益斜率为-20.84 dB/dec,相位裕度为46.62°,在Q点附近幅相特性曲线并无突变,系统稳定,电压的瞬态响应超调为45.6 mV,通过观察图9 示波器3通道PWM 的脉冲调整频率得到电压的响应时间22.54 μs,分别与无补偿时相比降低21.9%和63.9%。 表2 Type III 环路补偿理论设计参数 图8 Type III型环路补偿理论设计的幅相特性曲线 图9 理论设计环路补偿下输出电压动态响应 片外的补偿电路根据理论计算得到一定大小值的电容和电阻,在不同负载情况下,补偿效果也是不同的,负载的变换会使输出极点产生偏移,而零点则不会,在一定程度上会影响系统的响应速度和稳定性,采用Type III 环路补偿网络进行优化,使得整体环路相对于传统的Buck 电路片外补偿方案具有较好的动态响应速度和更好的稳定性。 通过参考图8 环路理论设计补偿幅相特性曲线图可知,其截止频率f0在开关频率的1/5 处附近,符合环路稳定判据中截止频率的下限,但较低的带宽会降低输出电压的动态响应速度和增加输出电压动态响应误差,扩展带宽可以有效地解决这一问题。极点在截止频率处引起的相位裕度θ 改变为: 由理论设计Type III 型环路补偿可知,极点fP2放置在开关频率的1/2 处,使增益曲线斜率向下转折-20 dB/dec,高频极点fP2的设计对截止频率的调整起着重要作用,由于高频极点fP2实际从极点的1/10 处就开始引入相移,由式(12)可知,将高频极点fP2右移至5 倍开关频率处,即可抵消其对截止频率的负面影响,从而扩展带宽[9]。 其Type III 环路补偿优化设计参数如表3 所示,其幅相特性曲线如图10 所示,其输出电压的动态响应如图11 所示,当开关电源环路补偿参数值为理论设计值时,其截止频率f0为80.74 kHz,增益裕度为0 dB 时的增益斜率为-20.84 dB/dec,相位裕度为74.12°,在Q点附近幅相特性曲线未突变,系统稳定电压的瞬态响应超调为38.8 mV,通过观察图11 示波器3通道PWM 的脉冲调整频率得到电压的响应时间为17.1 μs,分别与无补偿时相比降低33.6%和72.6%,与理论计算补偿值测试得到的数据相比降低14.9%和24%。 表3 Type III 环路补偿优化设计参数 图10 Type III型环路优化设计补偿时幅相特性曲线 图11 优化设计环路补偿下输出电压动态响应 本文设计了以UP1542 为电源转换芯片的电压模式Buck电路,提出了一种基于Type III 型环路补偿中零极点理论的优化方法,试验结果表明:所提基于Type III 型环路补偿中零极点理论的优化方法与Buck 电路无补偿方法和传统的电压模式Buck 电路Type III 环路补偿理论设计方法相比,输出电压超调显著降低,动态响应速度显著提升,同时保证了品质因素Q附近幅相特性曲线的稳定性,因此,更优地实现了零极点抵消,扩展了带宽,达到了提高电路稳定性的目的,验证了该优化方法的有效性。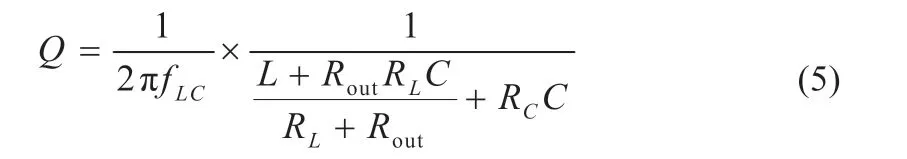
1.4 电压模式Buck 电路设计与试验结果分析

2 Type III 型环路补偿理论分析
2.1 Type III环路补偿的目的
2.2 环路稳定性判据
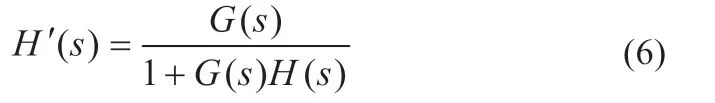
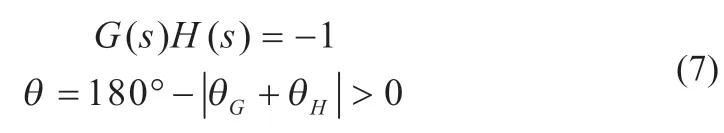
2.3 Type III型环路补偿理论设计与试验分析
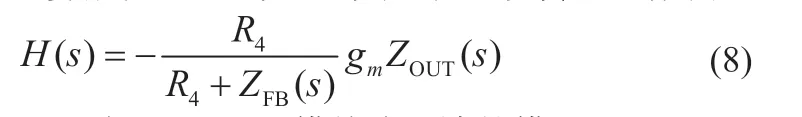
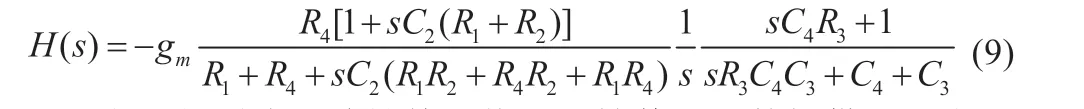
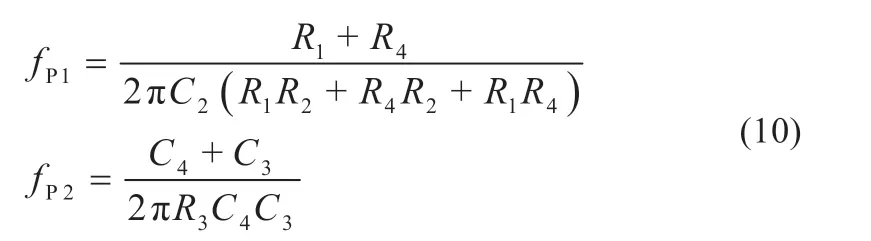
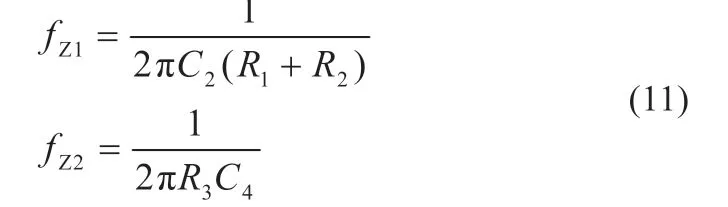
3 Type III 环路补偿网络设计优化与试验分析
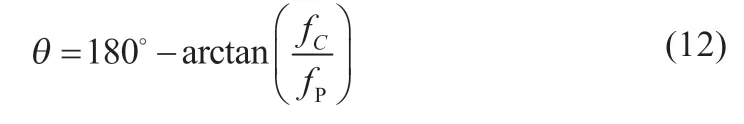

4 结束语

