含凹坑球壳剩余强度的试验研究和安全评定

陈虹港，李思源，张玉福，李祚成，苗世得

（1.机械工业上海蓝亚石化设备检测所有限公司，上海 201518；2.兰州石油机械研究所有限公司，甘肃 兰州 730050）

在承压设备中，球形构件因受力均匀而被广泛使用。对含表面缺陷的球壳构件，可将缺陷打磨并简化成球面凹坑，该凹坑具有各向受力基本相似的特点。对于含球面凹坑的球形容器，目前可以使用的安全评定方法主要有GB/T 19624—2019《在用含缺陷压力容器安全评定》［1］以及 API 579-1/ASME FFS-1—2007《Fit-for-Service》［2］。GB/T 19624—2019的球壳凹坑评定方法是以文献［3-4］中含球面凹坑球壳的屈服极限载荷计算值pL为依据，给出了含球面凹坑球壳屈服极限载荷剩余强度系数pL/poL（poL为无缺陷球壳的屈服极限载荷）。然后以球面凹坑无因次深度α及凹坑无因次长度 γ 之积 g（g=αγ）为参量，对 pL/poL数据进行拟合，得到了含凹坑球壳的评定计算式pL/poL=1－0.6g，此公式较简单。 但文献［3-4］中极限分析方法是以MELAN下限定理为基础进行优化的，而经典的极限下限定理要求同时满足平衡方程和屈服条件，给有限元分析带来较大困难，因此可能对屈服极限载荷计算结果的精度产生一定的影响。

文献［5］采用上限分析定理，应用数值方法计算了含球面凹坑球壳的极限载荷上限值。比较文献［4-5］的计算结果得到，对于相同尺寸的球壳凹坑，当球面凹坑的斜度小于1/3、相对深度大于0.5时，文献［5］的计算值比文献［4］的计算值大得较多。

Janelle J L［6］认为，在 ASME B31G—2009《Manual for Determining the Remaining Strength of Corroded Pipelines》［7］、BS 7910—2013《Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures》［8］和API 579-1/ASME FFS-1—2007等评定标准中，API 579-1/ASME FFS-1—2007的 2级评定方法较准确。但该方法只是一般评定原理，对含凹坑球壳构件列出了鼓胀系数计算式。

文献［9］采用 API 579-1/ASME FFS-1—2007中的2级评定原理和鼓胀系数计算式，应用数学分析方法，建立了含凹坑球壳评定的计算流程。用该方法计算了含球面凹坑球壳的剩余强度系数RSFA，有的凹坑的 RSFA比文献［1，4］的计算值pL/poL也大得较多。文献［9］还得出，当球壳凹坑的参量g＞0.3时，这些球壳凹坑的 RSFA都是 α和 g这 2个参量的函数；且当 g＞0.4时，GB/T 19624—2019中 pL/poL=1－0.6g的评定结果保守。到目前为止，还没有含球面凹坑球壳的试验数据可以检验上述几种评定计算方法的精确度。

为此，采用Q345D钢制作了2件无缺陷球壳试件和14件含球面凹坑球壳试件，对试件进行内压爆破试验，测定各试件失效的塑性最大压力和爆破压力，得到了含凹坑球壳试件塑性最大载荷剩余强度系数试验值RSFmt。应用试件的RSFmt检验文献［9］中的剩余强度系数计算方法。利用球壳和球面凹坑尺寸的参量α、g对文献［9］的计算值RSFA进行拟合，建立了含球面凹坑球壳的剩余强度系数RSF（α，g）计算式，应用该计算式建立了含凹坑球壳的爆破压力计算式，提出了含凹坑球壳的安全判据和含表面缺陷球形容器的安全评定方法。

1 含球面凹坑球壳爆破试验

1.1 试件设计

1.1.1 无缺陷球壳

无缺陷球壳试件的设计尺寸为，球壳外半径Ro=100 mm，球壳壁厚 t=10 mm。

1.1.2 含缺陷球壳

在球壳外壁设置球冠凹坑，外壁球冠的深度为 a，平面圆的直径为 2xo（图 1a）；在球壳外壁设置球面凹坑，球面凹坑的深度为a，表面圆的直径为 2xo（图 1b）；在球壳内壁设置球面凹坑，球面凹坑的深度为a，表面圆的直径为2xo（图 1c）。

1.2 试件制作

将φ210 mm的Q345D圆钢用数控机床加工成Ro=100 mm、t=10 mm的半球壳，再在半球壳的内、外表面分别加工球冠缺陷和球面凹坑，最后采用气体保护焊将相应的2个半球壳焊制成含凹坑球壳试件。

按照上述工艺制作了16件试件，其中无缺陷球壳试件2件、外壁含球冠凹坑球壳试件5件、外壁含球面凹坑球壳试件6件、内壁含球面凹坑球壳试件3件。16件球壳试件的几何尺寸和缺陷尺寸见表1。表1中pmaxt为试件的塑性最大压力，pomax为无缺陷时试件的塑性最大压力，pbt为试件的爆破压力，pb为爆破压力计算值，误差 η=（pbt-pb）/pbt×100%。

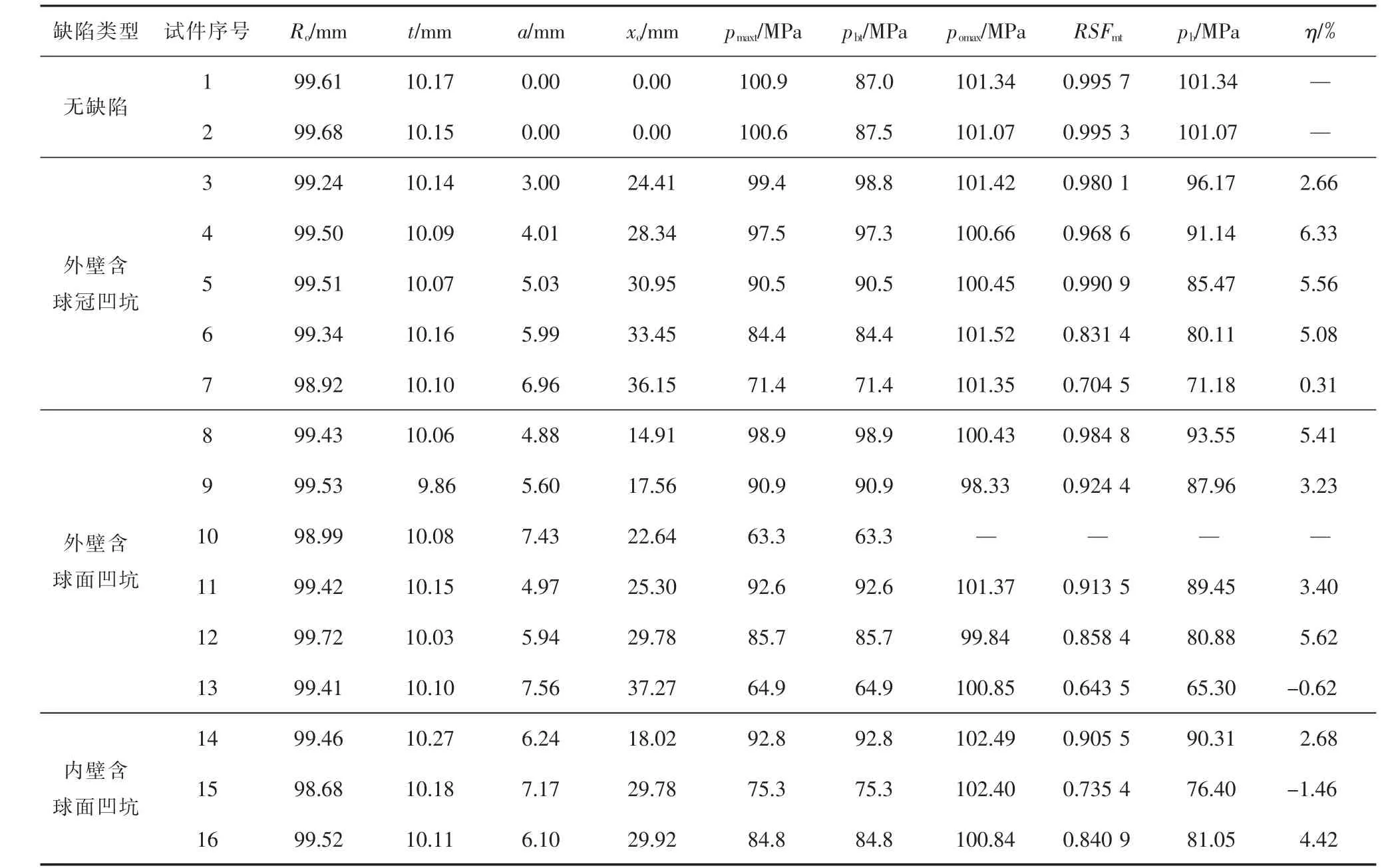
表1 球壳试件几何尺寸、缺陷尺寸和失效压力试验结果

1.3 试件材料力学性能

球壳试件材料为φ210 mm的Q345D圆钢，实测6组试件力学性能平均值，得到其屈服强度σs=292.8 MPa、抗拉强度 σb=496.3 MPa。

1.4 内压爆破试验

在球壳试件的外壁选定测试部位，对无缺陷球壳试件1和试件2，选取与接管距离最远的点及该点周边的点作为测试部位。对含凹坑球壳试件3～试件16，选取缺陷深度最大的点及周边的点作为测试部位。

在测试部位粘贴电阻应变片，采用电测方法对试件进行内压爆破试验，测定各测点的应变值和压力-应变曲线，直至有测点发生屈服。在球壳试件塑性屈服后，停止应变测量，再对试件连续缓慢升压，直至试件爆破，确定该试件的塑性最大压力pmaxt和爆破压力pbt。16个球壳试件的塑性最大压力pmaxt和爆破压力pbt结果见表1。

1.5 内压爆破失效分析

对无缺陷球壳试件，增压过程中压力先逐渐增大到最大值，之后压力逐渐降低至某个数值时试件发生爆破。爆破位置出现在壳体上，并远离焊缝和接头。破口显示为典型塑性破坏，能看到明显的剪切唇（图2a）。

对含缺陷球壳试件，增压过程中压力逐渐增大到最大值附近时其出现爆破，部分含缺陷球壳试件爆破压力略低于最大压力。含缺陷球壳试件的爆破位置均出现在缺陷中心附近，其中内壁含凹坑缺陷球壳试件15和外壁含球冠缺陷球壳试件4有碎片产生（图2b和2c），其余含缺陷球壳试件的破坏形式为刺漏（图2d）。

图2 不同球壳试件破口形貌

从表1的试验结果中发现，外壁含球面凹坑缺陷球壳试件10的爆破压力不合理。与外壁含球面凹坑缺陷球壳试件13相比，试件10的缺陷相对较小，但爆破压力却小于试件13的爆破压力，这可能是由于试件10材料本身存在缺陷或试件在加工过程中产生缺陷造成的。因此，在后续剩余强度系数计算方法与安全评定方法的研究中，舍弃试件10的试验数据。

2 含凹坑球壳试件剩余强度系数试验值

2.1 无缺陷球壳试件塑性最大压力

设球壳承受内压p，按GB 150.1～150.4—2011《压力容器》［10］，球壳应力 σ 计算式为：

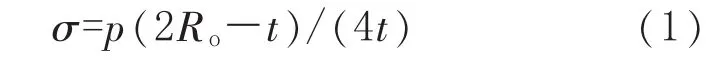
当σ达到球壳失效应力σf时，球壳的失效压力 pof为：

取球壳材料的抗拉强度σb作为球壳失效应力σf，代入式（2）得到球壳失效压力pob的计算公式为：

将表1中无缺陷球壳试件1的 Ro、t和σb的相应数值代入式 （3），计算得到试件1的失效压力pob=106.79 MPa。试件1的塑性最大压力pmaxt=100.9 MPa，pob比 pmaxt大 5.8%。 因此可以用式（3）近似计算无缺陷球壳的塑性最大压力pomax。为了提高计算结果的可靠性，对式（3）进行少许修正，用球壳外径 2Ro替代式（3）中的中径（2Rot），得到无缺陷球壳的塑性最大压力pomax计算公式为：

用式（4）计算得到各试件无缺陷时的塑性最大压力pomax，见表 1。从表 1看出，试件1和试件 2失效的塑性最大压力试验值与式（4）计算值的误差在0.5%以内。

2.2 塑性最大载荷剩余强度系数

含球面凹坑球壳试件的塑性最大载荷剩余强度系数试验值RSFmt定义为：

用式（5）计算得到含凹坑球壳试件的塑性最大载荷剩余强度系数试验值RSFmt，见表1。

3 一种剩余强度系数计算方法验证

3.1 GB/T 19624—2004计算方法

文献［4］采用参量g对含凹坑球壳的屈服极限载荷剩余强度系数pL/poL进行拟合，得到拟合计算式：

其中

GB/T 19624—2019采用式（6）计算含凹坑球形容器的极限载荷pL。

3.2 文献［9］计算方法

文献［9］利用精确的球面凹坑面积计算公式、API 579-1/ASME FFS-1—2007的 2级评定方法原理及球形构件鼓胀系数Mt，建立了含球面凹坑球壳剩余强度系数的计算流程。

3.2.1 计算流程Ⅰ

计算流程Ⅰ为计算外壁含球面凹坑球壳的剩余强度系数 RSFso。首先计算参量Ao、l和 r：

对给定的 xj=jxo/20（j=1，2，…，20），计算 RSFj：

其中

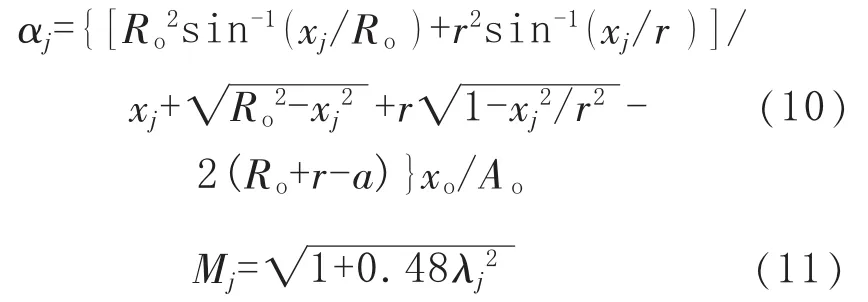
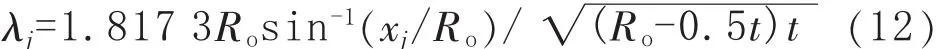
最后计算 RSFso，RSFso=min{RSF1，RSF2，… ，RSF20}。

3.2.2 计算流程Ⅱ

计算流程Ⅱ为计算内壁含球面凹坑球壳的剩余强度系数RSFsi。已知球壳内半径为Ri，首先计算参量 Aoi、li和 ri：

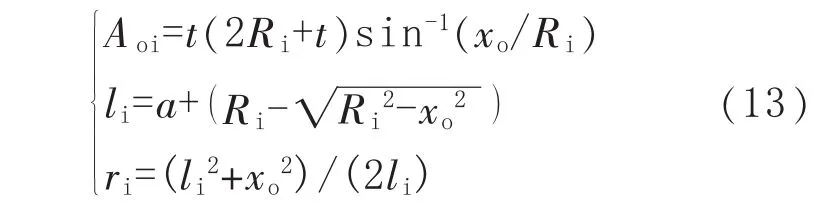
对给定的 xj=jxo/20（j=1，2，…，20），计算 RSFj：

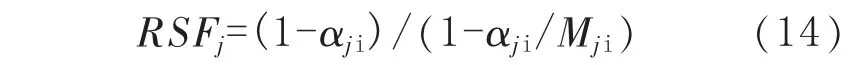
其中

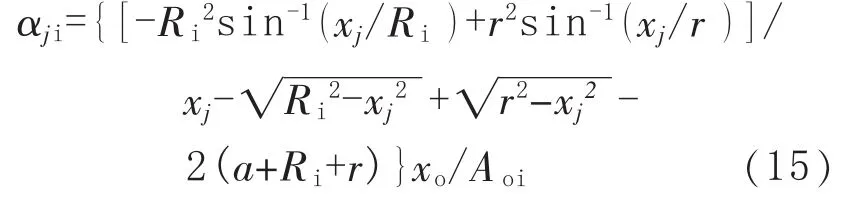
最后计算 RSFsi，RSFsi=min{RSF1，RSF2，…，RSF20}。

在计算流程Ⅰ和计算流程Ⅱ中，三角函数的角度单位均为弧度。

3.3 计算方法的验证

釆用表1中含凹坑球壳试件的塑性最大载荷剩余强度系数试验值RSFmt来检验3.2节中计算流程Ⅰ和计算流程Ⅱ的计算精度。含凹坑球壳的计算值和试验值比较见表2。表2中RSFs为计算流程Ⅰ或者计算流程Ⅱ计算的剩余强度系数，误差 ηs= （RSFmt-RSFs）/RSFmt×100% ，η′=［RSFmt-RSF（α，g）］/RSFmt×100%。

从表2可以看出，计算流程Ⅰ或计算流程Ⅱ的计算值RSFs大多比RSFmt小一些，且RSFs和RSFmt的误差ηs在-2.09%～9.05%。因此，计算流程Ⅰ和计算流程Ⅱ满足工程计算精度，计算结果可靠。

表2 含凹坑球壳剩余强度系数计算值和试验值比较

4 含球面凹坑球壳剩余强度系数RSF（α，g）拟合计算公式

文献［9］应用计算流程Ⅱ，计算了内壁含球面凹坑球壳的剩余强度系数RSFA，发现剩余强度系数RSFA是参量α（α=a/t）和 g的函数。文献［9］中含球面凹坑球壳剩余强度系数RSFA的计算数据见表3。

含球面凹坑球壳的剩余强度系数用参量α和 g 进行计算，记为 RSF（α，g）。

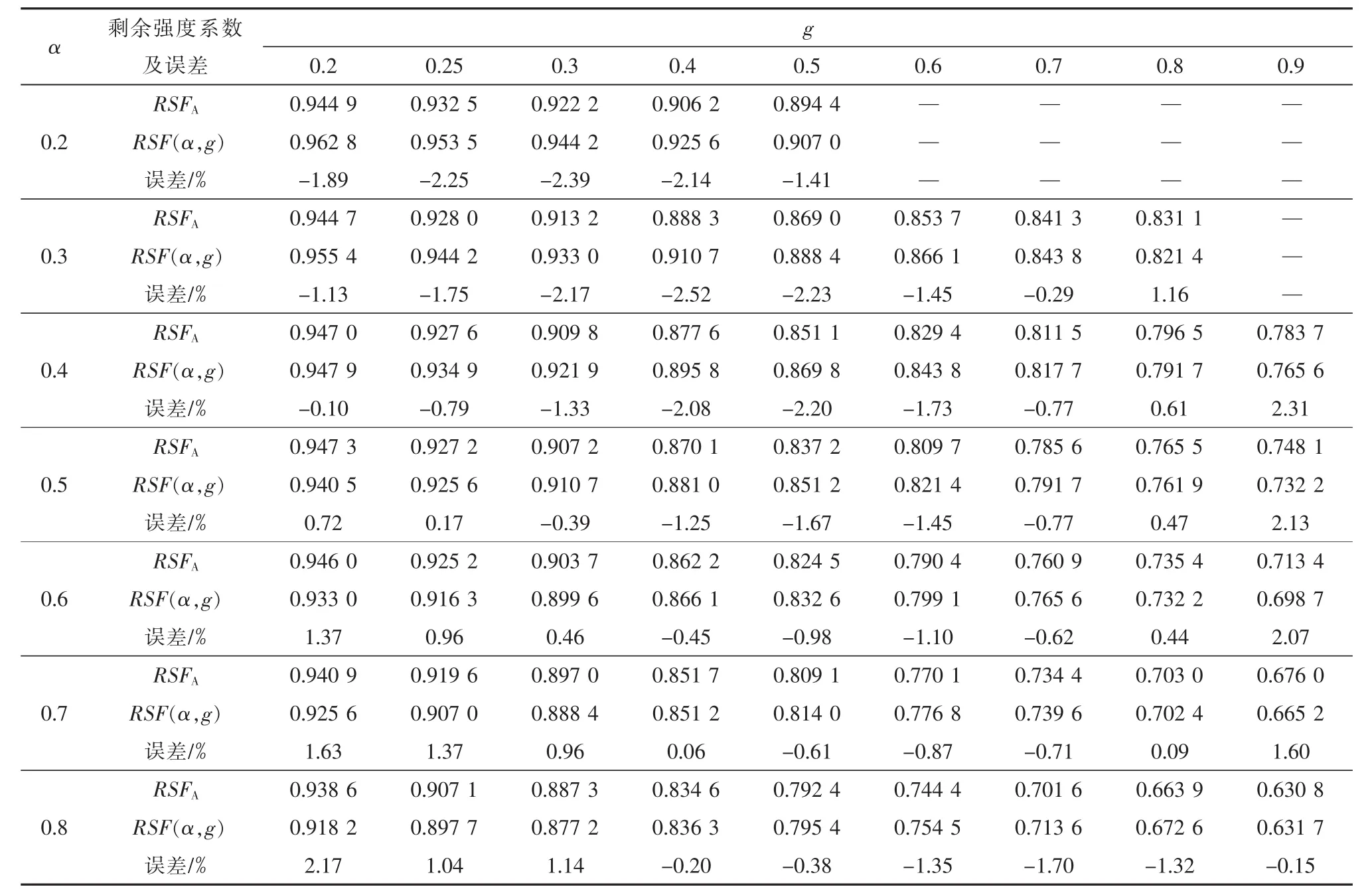
表3 含球面凹坑球壳剩余强度系数计算数据

4.1 α=0.7 时 RSF（0.7，g）计算式

将球面凹坑参量 α=0.7 时，表 3 中（α，g）为（0.7，0.2），（0.7，0.25），…，（0.7，0.9）所对应的RSFA值和g绘于平面直角坐标系g-RSF中，见图 3。

图3 α=0.7 时点（RSFA，g）拟合曲线

从 图 3 看 出 ， 点 （g，RSFA）， 即 （0.2，0.940 9）、（0.3，0.897 0）、（0.4，0.851 7）、 （0.5，0.809 1）、（0.6，0.770 1）、 （0.7，0.734 4）、 （0.8，0.703 0）、（0.9，0.676 0）都在直线 l附近，直线 l的斜率 k=－0.372。因此，对于α=0.7的球面凹坑球壳，其剩余强度系数 RSF（0.7，g）可用式（18）计算：

RSF（0.7，g）=1－0.372g （18）

4.2 g=0.8时 RSF（α，0.8）计算式

将球面凹坑参量 g=0.8时， 表 3中 （α，g）为（0.3，0.8），（0.4，0.8），…，（0.7，0.8）所对应的 RSFA值和α绘于平面直角坐标系α-RSF中，见图4。

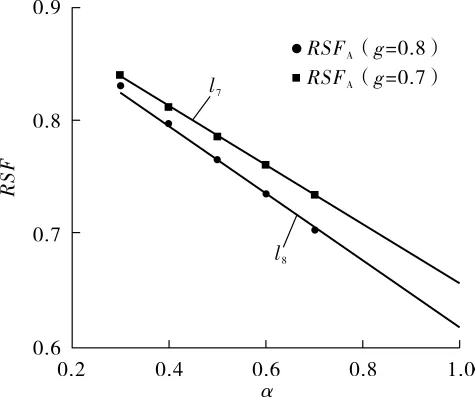
图4 g为 0.7和 0.8时点（RSFA，α）拟合曲线

从图 4 中可以看出，点（α，RSFA），即(0.3,0.831 1）、（0.4，0.796 5）、 （0.5，0.765 5）、（0.6，0.735 4）、（0.7，0.703 0） 都在直线 l8附近，直线 l8的斜率 k8=－0.372g=－0.297 6。因此，当g=0.8时，直线l8可作为上述5个点的拟合曲线，且有：

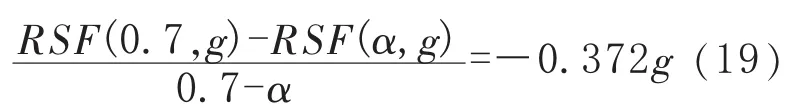
再将式（1 8）代入式（2 0）得到：

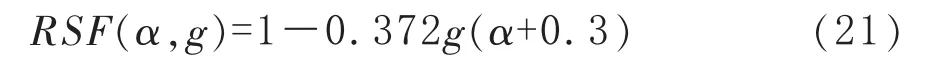
当g=0.8时，有：

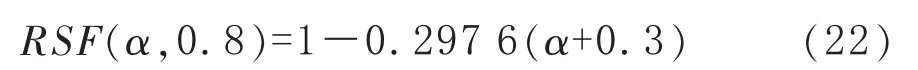
4.3 g=0.7时 RSF（α，0.7）计算式

将球面凹坑参量 g=0.7时， 表 3中 （α，g）为（0.3，0.7），（0.4，0.7）， …，（0.7，0.7） 所对应的RSFA值和α绘于平面直角坐标系α-RSF中，见图4。 从图 4 可看出，点（α，RSFA），即（0.3，0.841 3）、（0.4，0.811 5）、 （0.5，0.785 6）、 （0.6，0.760 9）、（0.7，0.734 4）都在直线l7附近，直线l7的斜率k7=－0.372g=－0.260 4。 因此，当 g=0.7 时，直线 l7可作为上述5个点的拟合曲线，且有式 （19）和（20）。 再将式（18）代入式（20）得到式（21），当 g=0.7时，有：

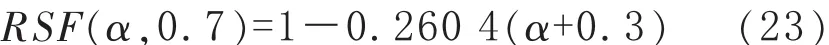
4.4 g为其他数值时 RSF（α，g）计算式

参照 4.2和 4.3的做法，当 g分别 0.6、0.5、0.4、0.3、0.2 时，RSF（α，g）都可用式（21）计算。

综上所述，对含球面凹坑球壳，当g为0.2，0.3，…，0.8 时，RSF（α，g）都能采用式（21）计算，式（21）中的 α≤0.8、g＜0.8。

应用计算流程Ⅰ和计算流程Ⅱ计算了内、外壁含球面凹坑球壳的剩余强度系数，结果表明，内、外壁含相同尺寸球面凹坑球壳的剩余强度系数计算值非常相近。因此，拟合公式（21）对内、外壁含球面凹坑球壳的剩余强度系数计算都适用。

5 含凹坑球壳剩余强度系数计算式（21）的验证

5.1 用表3中的RSFA验证

对表3中α和g所对应的球面凹坑球壳，应用式（21）计算其剩余强度系数 RSF（α，g），得到的结果见表3。从表3看出，式（21）的计算值RSF（α，g）与 RSFA的误差都在－2.5%～2.3%。因此，可用式 （21）简便替代计算流程Ⅰ和计算流程Ⅱ中的计算方法。

5.2 用塑性最大载荷剩余强度系数试验值RSFmt验证

采用式（21）计算表2中13个含球面凹坑球壳试件的剩余强度系数 RSF（α，g），结果见表 2。从表 2 看出，式（21）的计算值 RSF（α，g）与试验值 RSFmt的误差 η′ 在－1.45%～6.52%，绝大多数试件的计算值 RSF（α，g）都小于试验值RSFmt，且13个试件的误差绝对值平均为3.66%。因此，用式 （21）计算含球面凹坑球壳的剩余强度系数RSF（α，g）是可靠的，而且具有满意的计算精度。

6 含凹坑球壳爆破压力计算和安全判据

6.1 爆破压力计算

应用式（21）得到含球面凹坑球壳的塑性最大载荷pmax计算式：

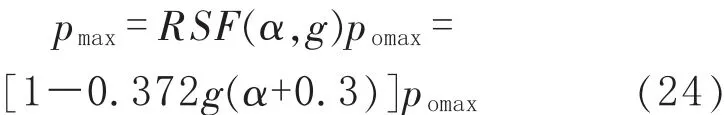
根据剩余强度系数的定义，应有RSF（α，g）≤1。从表1的试验数据看出，无缺陷球壳试件和含凹坑球壳试件的球壳外径与壁厚都分别相近，但在14个含凹坑球壳试件中，有7个试件的爆破压力大于无缺陷球壳试件的爆破压力，而且有些大了10%以上。因此不能用无缺陷球壳试件的爆破载荷定义含凹坑球壳试件的剩余强度系数。

比较表1中含球面凹坑球壳试件的pmaxt和该试件的pbt发现，在 14个试件中，12个试件的pmaxt=pbt， 只有 2个试件 （试件 3和试件 4）的pmaxt＞pbt，但这 2 个试件的 pmaxt≤1.005pbt。 因此，对于表1中14个含凹坑球壳试件，均有pbt≈pmax。再应用式（24），得到含球面凹坑球壳构件的爆破压力pb近似计算式：

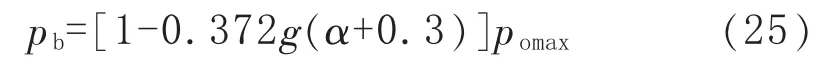
当无缺陷球壳的塑性最大压力采用式 （4）计算时，含球面凹坑球壳构件的爆破压力pb可用下式计算：

取球壳材料的抗拉强度σb=496.3 MPa，应用式（26）计算了表 1中 13个试件的爆破压力 pb，结果见表1。从表1中看出，式（26）的计算值 pb和试件的爆破压力pbt的误差 η在－1.46%～6.33%，误差绝对值平均为3.65%。

6.2 安全评定判据

在GB 150.1～150.4—2011中，对碳素钢和低合金钢，材料的许用应力［σ］取 σb/2.7，σs/1.5，…中的最小值。压力容器构件的许用压力［p］也可类似选取，当压力构件的爆破压力为pb时，为了确保容器安全运行，该构件的许用压力［p］取：

对于含球面凹坑球壳，计算得到α和g后，该球壳的爆破压力pb可用式（25）计算。将式（25）代入式（27），得到该球壳的许用压力［p］为：

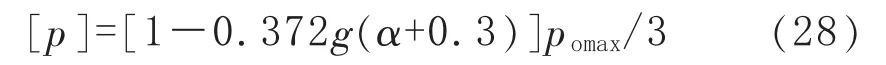
6.2.1 判据1

对含球面凹坑的球壳构件，其无缺陷球壳的塑性最大压力为 pomax，用式（7）计算 g，且 α=a/t。若球壳的工作压力p满足式（29），则该球壳构件是安全的。

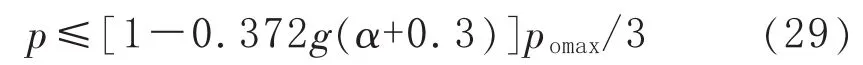
6.2.2 判据2

当采用式（26）计算含球面凹坑球壳构件的爆破压力pb时，可得到安全判据2。对含球面凹坑的球壳构件，用式（7）计算g，且α=a/t。若球壳的工作压力p满足式（30），则该球壳构件是安全的。

对含球面凹坑球壳构件，当其g≤0.25、α≤0.77时，用式（21）计算得到的球壳剩余强度系数RSF（α，g）都有：

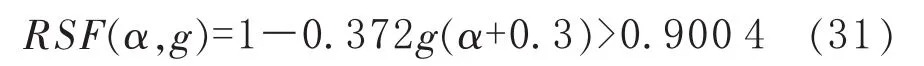
式（31）满足 API 579-1/ASME FFS-1—2007中的安全条件RSFa=0.9，因此该球壳安全。

6.2.3 判据3

对含球面凹坑的球壳构件，用式（7）计算g，且 α=a/t。若 g≤0.25、α≤0.77，则该球壳构件是安全的。

7 球形容器安全评定方法

应用安全评定判据2和判据3，可以得到球形容器表面缺陷的安全评定方法。

评定的球形容器球壳外半径为Ro，壁厚为T，球壳运行到下一次检验周期的壁厚腐蚀余量为C0。球壳的评定壁厚t=T－C0，参量α、g按下式计算：

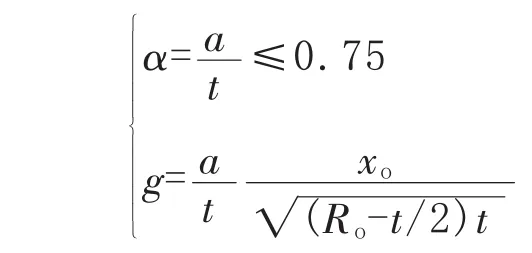
α、g和工作压力p符合下列条件之一，则该球形容器是安全的，①g≤0.25。②当0.25＜g≤1时，p≤2σbt［1－0.372g（α+0.3）］/（3Ro）。③ 当 g＞1 时，用计算流程Ⅰ或计算流程Ⅱ计算剩余强度系数RSFs，且 p≤2σbtRSFs/（3Ro）。

8 结语

（1）采用 Q345D制作含凹坑球壳试件，在内压试验下测定试件的塑性最大压力和爆破压力，得到了含凹坑球壳试件塑性最大载荷剩余强度系数的试验值RSFmt。

（2）用 API 579-1/ASME FFS-1—2007的 2级评定方法建立的计算流程Ⅰ和计算流程Ⅱ计算的试件RSFs，与该试件的试验值RSFmt符合较好。

（3）对采用计算流程得到的计算值RSFA进行拟合，得到含球面凹坑球壳剩余强度系数拟合计算式，即式（21），其计算值都能满足工程计算精度要求。含凹坑球形容器的爆破压力pb可以采用式（25）和式（26）计算。

（4）提出了含凹坑球壳的安全判据，依据安全判据得到了含表面缺陷球形容器的安全评定方法。