基于大涡模拟的输油泵性能预测及内流场分析

张 兴，孙 宇，毛艳虹，王文博

（1.国家管网集团 北方管道公司 管道科技研究中心，河北 廊坊 065000；2.国家能源油气长输管道技术装备研发 （试验）中心，河北 廊坊 065000；3.国家管网集团 北方管道公司有限公司 秦皇岛输油气分公司，河北 秦皇岛 066004；4.江苏大学，江苏 镇江 212013；5.国家管网集团 山东输油有限公司，山东 日照 276800）

输油泵是石油化工等行业中重要的动力设备，其性能对整个原油运输系统有重要影响。随着石油工业的发展，输油泵的选型、安全性和节能技术引起了众多学者的关注［1-3］。 张燕斌等［4］通过试验测试分析了不同运输介质下输油泵的振动情况，最后得出输送汽油时泵振动幅度比输送柴油大的结论。Lin W B等［5］探究了在长距离输油系统中油泵的振动情况，研究结果表明，油泵的振动程度与油品种类相关，轻质油的振动最明显，相邻的泵一起运行时振动最剧烈。欧永红等［6］对输油泵运行过程中可能会出现的故障进行了分析，并针对故障原因给出了相应的解决对策。魏升龙等［7］通过分析双吸泵的结构特点，探究了炼油装置中双吸泵的安放位置以及注意事项。He Shanghong等［8］以变排量叶片油泵为研究对象，探究了温度对油泵泄漏量的影响，结果表明温度越低，泄漏量越小。

近年来，计算流体力学（CFD）技术日益成熟，成为了可以有效预测泵性能和内部流动特性的方法。为探究转子与泵体的径向间隙对泵流动特性的影响，代光辉等［9］应用FLUENT软件对不同间隙的输油泵进行数值模拟计算，发现泵出口压力随着间隙增大而逐渐减小。傅剑辉等［10］采用FLUENT软件研究了几个关键因素对中开式输油泵数值计算的影响，经过对比发现，速度进口和自由出流的边界条件更易收敛。谭东杰等［11］基于FLUENT软件研究了导叶与叶片数的匹配关系对中开式输油泵的影响，研究表明，导叶相位角为30°、导叶叶片数为10时输油泵的效率最高。晁文雄等［12］采用大涡模拟（LES）湍流模型对多工况的燃油离心泵进行数值模拟分析，结果表明燃油离心泵在大流量和高转速时运行更稳定。宋冬梅等［13］采用ANSYS CFX软件对双吸离心泵进行数值模拟，并将预测的计算值与试验值进行对比，发现模拟结果与试验结果一致。曾维国等［14］对设计工况下的双吸油泵进行非定常数值计算，计算结果表明，叶轮与蜗壳的动静干涉对隔舌断面附近的涡型影响较大，蜗壳扩散段内的静压受叶轮和蜗壳的动静干涉出现周期性波动变化规律。白利等［15］研究了不同流量工况下双吸泵的湍流流场，研究结果发现，湍动能在设计工况下最小，涡黏系数的变化与湍动能的变化规律一致。李永乐等［16］对双吸输油泵进行了数值模拟，分析了其压力和速度分布规律，并通过试验验证了模拟的准确性。张凤丽等［17-25］对输油泵的性能及流动进行了研究分析。

文中以一输油泵为例，采用ANSYS CFX软件，对设计工况下该输油泵的性能和内部流场进行预测分析。

1 输油泵性能计算模型

输油泵设计体积流量3 100 m3/h，设计扬程190 m，转速2 990 r/min，比转速 140。两叶轮背靠背对称布置，叶轮进口直径250 mm，叶轮出口直径436 mm，叶轮叶片数为6片，导叶叶片数为10片。通过Pro/E软件分别对输油泵全流道计算域的进口延长段、吸水室、叶轮、导叶、蜗壳和出口延长段进行建模，见图1。

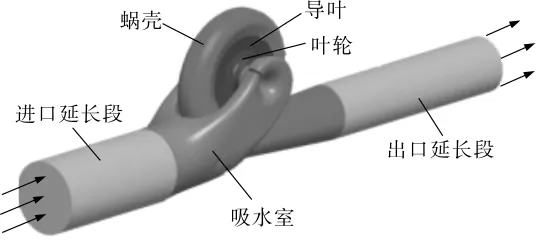
图1 输油泵全流道计算域模型

采用ICEM软件对输油泵计算域进行网格划分，主要部件叶轮、导叶和蜗壳的网格划分见图2。输油泵计算域模型总网格数为1.25亿，各部件网格信息见表1。

图2 输油泵计算域主要部件网格划分

表1 输油泵计算域各部件网格信息

2 输油泵性能计算方案

2.1 湍流模型及控制方程

对输油泵模型先进行稳态计算，以稳态计算结果为初始值进行瞬态计算。

稳态计算选取k-ω（k为湍动能，ω为比耗散率）湍流模型，瞬态计算选取LES湍流模型，亚格子模型选用WALE。

2.1.1 k-ω湍流模型

k-ω湍流模型描述了基于湍动能k和比耗散率ω的输运方程，其输运方程为：

式中，k 为湍动能，m2/s2；ω 为比耗散率，1/s；t为时间，s；xi、xj分别为 i方向、j方向的矢量；ρ为流体密度，kg/m3；ui为速度，m/s；Гk为湍动能扩散系数；Gk、Yk、Sk、Gω、Yω、Sω、Dω为相关产生项及用户自定义源项。

2.1.2 LES湍流模型

LES湍流模型是一种介于直接数值模拟模型和雷诺平均模拟模型之间的湍流模型，其对瞬态N-S方程进行滤波处理，对于网格尺度大的湍流运动通过N-S方程直接计算，对于小尺度涡则通过模型体现。经滤波处理的控制方程表示如下。

连续方程：

动量方程：

其中

2.2 边界条件和求解设置

输油泵计算模型入口处采用压力进口边界条件，出口处采用质量流量出口边界条件，壁面边界定义为无滑移粗糙壁面，粗糙度为0.25 μm。计算介质为油，其密度为 840 kg/m3、动力黏度为1 340×10-5Pa·s。稳态计算采用高阶求解模式，最大迭代步数为2 000，收敛精度为10-6。瞬态计算时间步长2.78×10-4s（即叶轮旋转1°所用的时间），共计算5个旋转周期。

3 输油泵性能计算结果分析

3.1 外特性分析

输油泵的扬程H、效率η计算公式分别为：

式中，pout为输油泵出口总压，pin为输油泵进口总压，Pa；g 为重力加速度，m/s2；Δz为进出口高度差，m；qV为当前工况的体积流量，m3/s；M 为作用在叶轮表面的力矩之和，N·m；Ω为叶轮旋转角速度，rad/s。

经数值模拟计算，该输油泵计算扬程为205 m，满足设计相关要求，可见LES可以较好地预测该输油泵的性能。

输油泵水力部件效率计算结果见表2。从表2可以看出，吸水室水力损失很小，效率较高，达99.87%。叶轮的效率接近95%，说明吸水室与叶轮的水力模型匹配较理想。导叶的效率较其他部件效率偏低，但仍超过90%，蜗壳效率损失也在正常范围内。

表2 输油泵水力部件效率计算结果

3.2 内流场分析

3.2.1 y+分布

y+表示量纲一壁面距离，直接影响第一层网格节点位置。在CFD计算中，LES对壁面网格要求较高，第一层网格节点在壁面的黏性底层，即要求y+＜1。

输油泵叶轮叶片y+分布见图3。由图3可知，叶轮叶片壁面的y+均小于1，满足要求。

图3 输油泵叶轮叶片y+分布

3.2.2 压力分布

设计工况下不同湍流模型计算得到的输油泵全流道中间截面压力分布情况见图4，叶轮和导叶中间截面压力分布见图5。

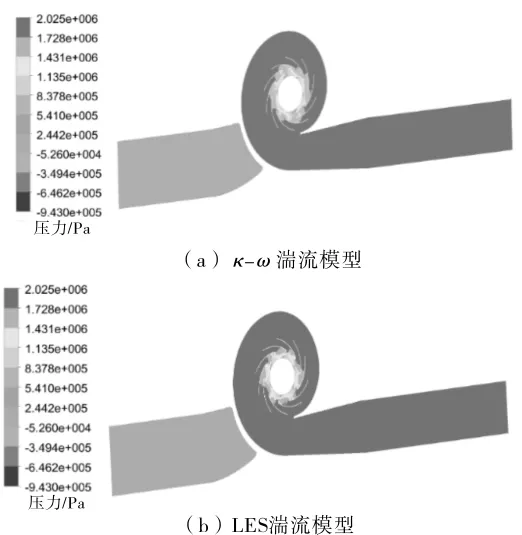
图4 设计工况下不同湍流模型计算得到的输油泵全流道中间截面压力分布

从图4看出，2种湍流模型计算得到的压力分布趋势相同，均为进口处压力低，出口处压力高。

分析图5可以发现，由于叶轮旋转做功，叶轮流道内液体压力沿着径向逐渐增高，变化梯度平稳，在叶轮与导叶交汇处达到最大值。随着导叶流道的过流面积逐渐增大，动能转化为压能，压力在导叶流道内进一步升高，因此导叶出口边压力高于进口边压力。压力梯度变化最大出现在叶轮与导叶交汇处，预示此处损失严重。对比图5a、图5b可知，相较于k-ω湍流模型，LES湍流模型计算得到的从叶轮到导叶的压力变化梯度更明显。

3.2.3 速度分布

设计工况下不同湍流模型计算得到的输油泵全流道流线图见图6。

图5 设计工况下不同湍流模型计算得到的输油泵叶轮和导叶中间截面压力分布

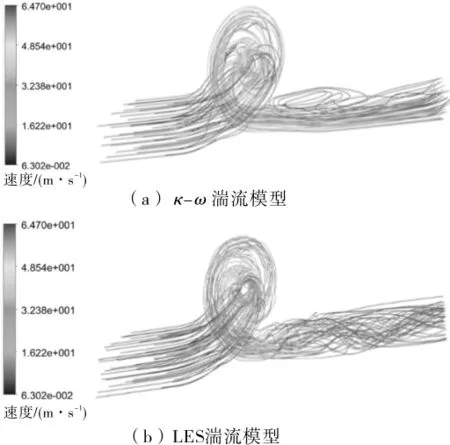
图6 设计工况下不同湍流模型计算得到的输油泵全流道流线图

由图6可以看出，全流道进口段流线平稳，出口段流线较紊乱，LES湍流模型计算得到的出口段紊乱程度比k-ω湍流模型的严重。

设计工况下不同湍流模型计算得到的输油泵全流道中间截面相对速度分布见图7。从图7a可以发现，采用k-ω湍流模型计算得到的叶轮、导叶、蜗壳附近相对速度变化较均匀。而图7b显示，在叶轮、导叶和蜗壳附近出现许多小涡，可见采用LES湍流模型计算能更真实地反映输油泵内部的流动情况。

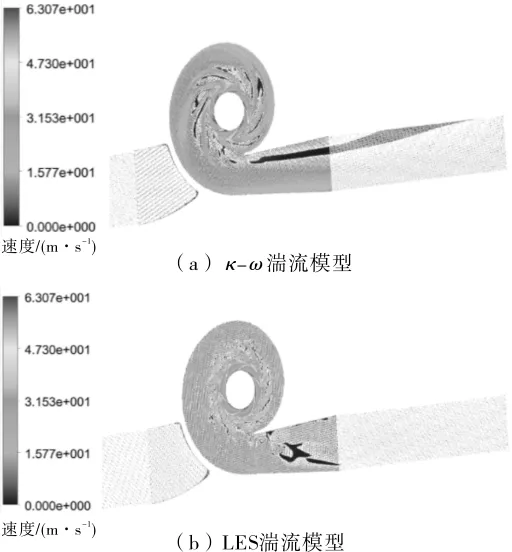
图7 设计工况下不同湍流模型计算得到的输油泵全流道中间截面相对速度分布

为进一步了解叶轮和导叶内部的流动情况，给出了设计工况下不同湍流模型计算得到的叶轮和导叶中间截面的相对速度分布，见图8。从图8可以看出，叶轮内相对速度比导叶的大，叶轮叶片出口处的相对速度大于叶片进口处的，LES湍流模型计算得到的相对速度分布更清晰。

图8 设计工况下不同湍流模型计算得到的输油泵叶轮和导叶中间截面相对速度分布

从图9所示的导叶叶片绝对速度流线局部放大图也可以看出，LES湍流模型能较好地反映出分离流动，导叶流道内漩涡主要由叶片前缘诱导产生，并沿着导叶流道向下游延伸和发展。

图9 设计工况下不同湍流模型计算得到的输油泵导叶叶片绝对速度流线局部放大图

4 结语

采用ANSYS CFX软件，分别应用k-ω湍流模型和LES湍流模型对设计工况下的输油泵进行性能预测和内部流场分析，分析结果表明，①采用LES湍流模型模拟计算得到的输油泵扬程符合设计要求，各部件水力效率较高。因此采用CFD技术进行泵的性能预测以及优化设计具有一定的参考意义。②输油泵叶轮进口处压力低，导叶出口处压力高。通过LES湍流模型计算得到的叶轮内低压区范围更大，叶轮出口处到导叶进口处的压力过渡更均匀。③在叶轮和蜗壳处，应用LES湍流模型得到的内部流动情况比k-ω湍流模型的更符合实际。采用LES湍流模型计算可以明显看到叶轮叶片出口处形成的速度涡。