点电荷在接地金属球形空腔内的电场分布

陈晓平 谢元栋

(华南师范大学物理与电信工程学院 广东 广州 510006)

本文讨论的金属空腔表面为球面．为方便起见，球壳厚度不计．根据镜像法，可以求解出点电荷在接地导体球壳内的电势、电场强度分布的解析式．利用Mathematica强大的数值计算能力，探讨解析式背后的物理意义．在点电荷和感应电荷共同激发的电场中，考虑相对论效应，讨论点电荷在球壳中静止释放的运动情况．

1 电势和电场强度公式推导

如图1所示，点电荷在x轴上距球心b的位置，r与x轴的夹角为θ．镜像电荷在x轴上距球心d的位置．导体球壳接地，半径为a．

图1 电势和电场强度公式推导情境图

由唯一性定理和镜像法[1]可知

(1)

所以

(2)

即

(3)

由余弦定理可得

(4)

(5)

联立上式可得

q′2(b2+a2-2abcosθ)=

q2(d2+a2-2adcosθ)

(6)

式(6)在任意角度下都应该成立，所以有

q′2(b2+a2)=q2(d2+a2)

(7)

2abq′2=2adq2

(8)

解得

(9)

d2=b(不符合实际情况，舍去该解)

(10)

(11)

综上，接地导体球壳内的电势分布为

(12)

如图1所示，在直角坐标系下，r2=x2+y2+z2，x=rcosθ，电场强度的各个分量为

(13)

(14)

(15)

由于球壳表面各点电势梯度与r反向，所以

(16)

总的感应电荷为

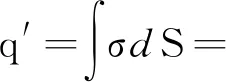
-q

(17)

若将点电荷从静止释放，点电荷会朝着球壳内表面做变加速运动，甚至会出现接近光速的现象，此时应考虑相对论效应[2]．基于以上讨论，点电荷运动到位置x处时，镜像电荷的大小和位置如下

点电荷和球壳之间的相互作用力可以等效为点电荷与镜像电荷之间的电像力．则有

(18)

根据相对论公式

(19)

(20)

联立式(18)、(19)、(20)，得到

(21)

(22)

解得

v=

(23)

其中

运动方向朝着x轴正方向．

2 电势和电场强度分布

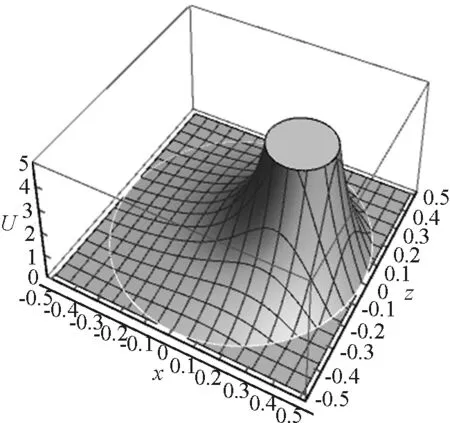
图2 电势分布图

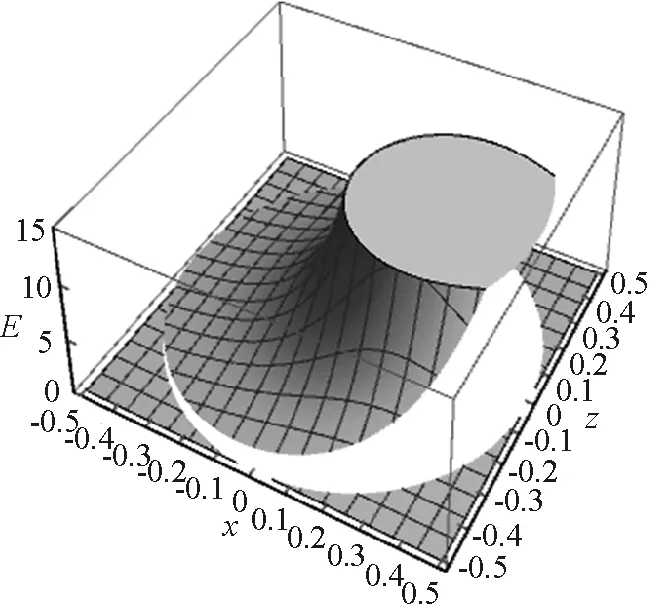
图3 电场强度分布图

图4 电场强度方向分布图

图5 等势线图

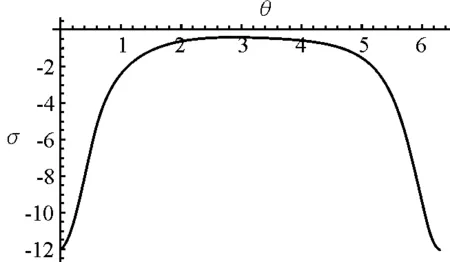
图6 电荷面密度分布图

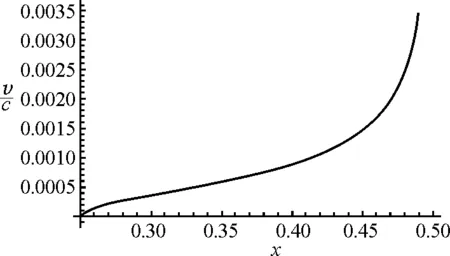
图7 速度-位置关系图

由于这里采用了点电荷模型，当坐标趋近于点电荷时，电势趋于无穷大．但是图形只能画出有限值，所以Mathematica会在有限范围内自动截断[3]．

这里点电荷是放置在x=0.25，z=0处．

在电势分布图中，球壳内电势大于零，球壳外电势为零，电势在球面处连续分布．球壳内表面靠近点电荷的一侧电势显著大于远离点电荷的一侧．在等势线图中，可以清楚看到球壳内靠近点电荷附近的等势面更为密集．

在电场强度分布图中，球壳内电场强度均大于零，球壳外电场强度均为零，电场强度在球面处并不连续分布．所以电场强度分布并没有像电势分布图那样，在球面处闭合，而是出现了“空白”．球壳内表面靠近点电荷的一侧电场强度显著大于远离点电荷的一侧，说明靠近点电荷的球壳内表面处感应电荷的绝对值较大，而在远离点电荷的球壳内表面处只有少量的感应电荷．

在电场强度方向分布图中，电场线没有穿透球壳，球面为等势面．从图中的箭头方向，不难看出感应电荷均为负电荷．

感应电荷面密度受到角度θ变化的影响，感应电荷分布关于x轴对称．在θ=0处，也就是球壳内表面距离点电荷最近的地方，可以取得最大值．这与前面分析所得情况也是符合的．

在速度-位置关系图中可以看出，点电荷在向接地导体球壳运动时，速度不断增大，速度的变化率也迅速增大．

3 结论

基于理论推导和数值积分绘图，我们可以得出一致的结论：点电荷在接地导体球壳内时，内表面感应电荷均为负电荷．球壳内表面靠近点电荷一侧的电荷面密度的绝对值明显较大．所以电场大多集中在球壳内靠近点电荷的一侧．

在点电荷和球壳内表面感应电荷共同激发的电场中，若将点电荷静止释放，将做加速度增大的变加速运动．