不同剪切模式下的全尾砂浆触变特性研究
甘德清,常英杰,张友志,薛振林,刘志义
(1.华北理工大学矿业工程学院,河北 唐山 063210;2.河北省矿业开发与安全技术重点实验室,河北 唐山 063210)
随着国家对环境保护重视程度的提升,以及“绿水青山就是金山银山”理念的提出,国家对矿山环境的监管力度不断加强,尾砂胶结充填技术的重要性日益凸显,充填技术也在各大矿山中广泛应用[1]。因为料浆需要输送到井下进行充填,所以充填技术中的管道输送问题非常重要,尾砂料浆在管道输送过程中的一般规律问题也亟需解决。其中,管道输送过程中料浆的触变特性研究尤为重要,其有助于管道输送设备及搅拌装置的研究与开发,对于充填系统的进一步优化有极大作用。对于固液两相流的触变特性研究,一些专家学者在混凝土研究方面取得了一定成果。AHARI等[2]采用不同的辅助胶凝材料对混凝土的触变性和破坏行为进行了研究,结果表明除了高炉矿渣(BFS)外,与只含硅酸盐水泥的混合物相比,在混凝土中使用胶结材料可使其触变值升高;HOWARD[3]对触变性发展的历史和当今科学界对其理解进行了阐述;ROUSSEL等[4]发现最大的临界应变与水泥颗粒间的胶态相互作用有关,而最小的临界应变与早期水合物有关,它们优先形成于水泥颗粒间的接触点。
近些年来,众多专家学者从不同角度展开了对充填尾砂料浆的触变特性研究。朱世彬等[5]对不同骨料比的料浆流变特性随时间的变化规律展开了研究,得出了塑性黏度和屈服应力随时间的变化公式;张友志等[6]利用浆式流变仪研究了充填料浆在不同情况下的触变行为,并提出了基于量纲分析的触变特性预测模型;梁冰等[7]利用凹凸棒石为改性剂研究了凹凸棒石对充填料浆触变性的影响,提出凹凸棒石掺量越高,料浆触变性越大,屈服系数与动态屈服应力也随之增加,流动性降低;刘晓辉等[8]通过尾砂料浆的静置恢复实验得出,尾矿质量分数、剪切速率,以及絮凝剂的添加量对充填料浆的触变特性均有不同程度的促进作用,而在静置条件下,料浆质量浓度越高,其絮网结构的恢复速率则越快;杨柳华等[9]针对膏体搅拌过程中的触变性,对搅拌后料浆展开静置恢复试验,并提出料浆体系中的超细物料是产生触变性的关键因素,灰砂比及料浆质量分数也是影响触变性的重要因素;薛振林等[10]采用正交设计方法分析了灰砂比、质量浓度和温度对流变参数的影响规律,得出料浆的屈服应力影响权重从高到低依次为质量浓度、温度、灰砂比;闫泽鹏等[11]利用Comsol软件建立管道输送模型,得出最佳输送管径为160 mm和180 mm,浓度为68%~70%;甘德清等[12-13]对充填料浆管道阻力损失影响因素进行分析发现管道阻力损失与管径呈反比例函数关系,料浆浓度越高,管道阻力损失越大,通过控制剪切速率的方法研究不同质量浓度,不同灰砂比充填料浆的流变特性,发现料浆流变曲线适合用宾汉塑性体的流变特征来描述;吴再海等[14]通过不添加和添加不同比例减水剂的流变特性试验得出减水剂添加量为0.5%时为曲线拐点,此时料浆表现较好效果。
前人对充填尾砂料浆触变性的研究多针对其物料组成,从而去探究其触变特性的内在规律,但是对触变性本身在管道输送过程中的变化规律研究较不明确,因此,本文以河北省某铁矿全尾砂为物料,根据充填尾砂料浆管道输送过程中管道的变化,采用不同剪切模式对充填料浆进行试验,从而得出充填尾砂料浆在不同剪切模式下触变性的一般规律,为现场管道输送过程的优化提供一定的理论依据。
1 试 验
1.1 试验材料
以河北省某铁矿全尾砂为材料,经测试,尾砂的比重为2.73 t/m3,利用NKDG100-D型激光粒度分析仪对其粒径进行测试,粒级分布如图1所示。由图1可知,该尾矿全尾砂74 μm以上粒径占比远超过75%,按照尾砂粒径分类标准,该尾砂为极粗尾砂。 试验用水泥为矿渣硅酸盐水泥(P.S.A32.5),试验用水为实验室自来水。
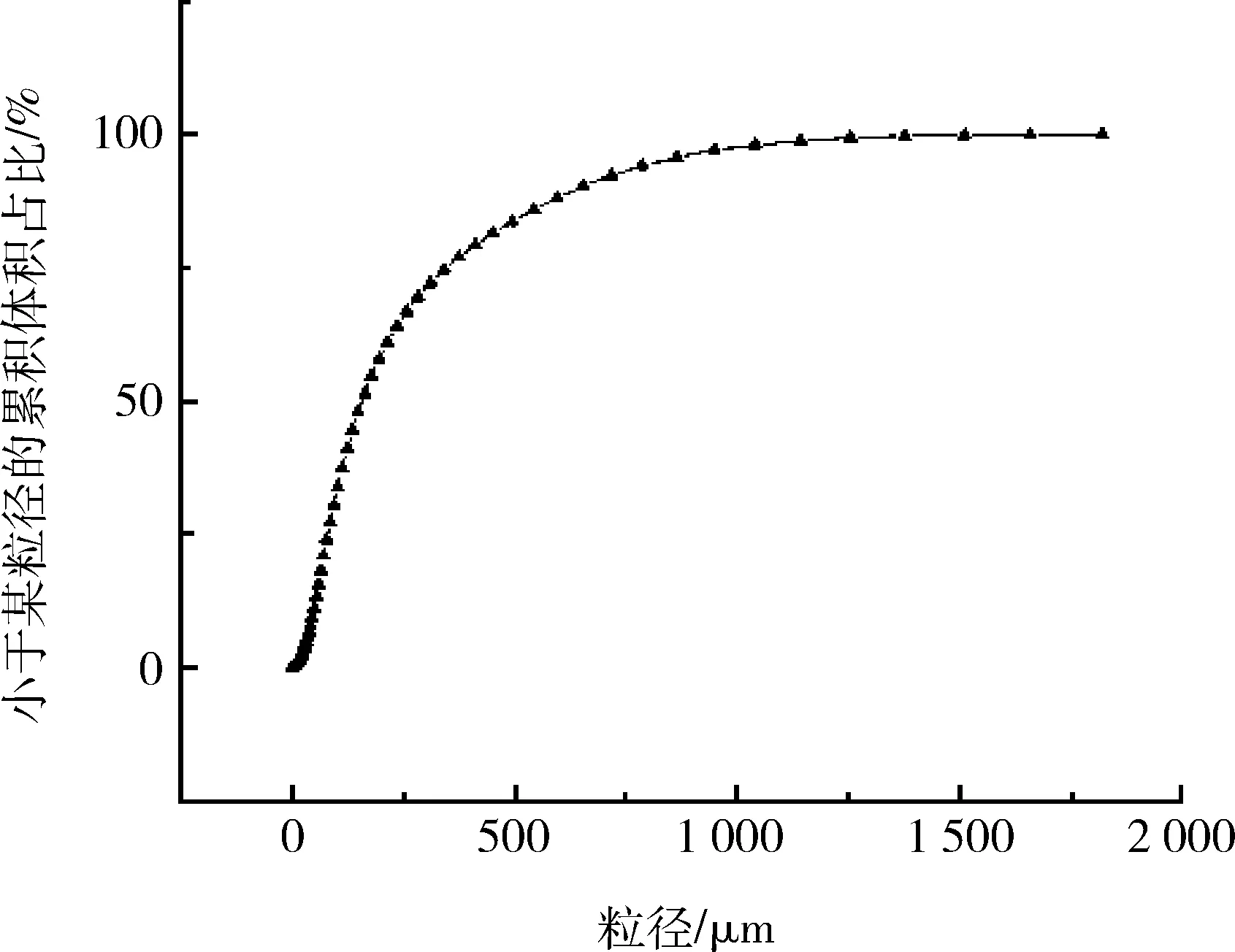
图1 尾砂粒级分布曲线
1.2 试验设备
流变试验所用设备为美国的赛默飞世尔科技公司生产的便携式流变仪HAAKE Viscotester iQ,配备转子为FL 22 4B/SS 01140879的四叶桨式转子。
1.3 试验方案
考虑到料浆的流动性,经过前期测试,确定灰砂比为1∶4,质量浓度为66%。为探究充填料浆在不同剪切模式下的触变行为,将剪切模式分为恒定剪切模式、环形剪切模式以及阶跃剪切模式。试验采用CR测试方法进行流变测试,由于在剪切过程中料浆的剪切应力是不断变化的,所以认为在剪切应力进入较为稳定阶段时的应力为屈服应力。试验方案见图2~图4。

图2 恒定剪切

图3 环形剪切

图4 阶跃剪切
恒定剪切模式是使充填料浆在持续恒定的剪切速率下进行剪切,使用同一配比的砂浆在剪切速率分别为30 s-1、60 s-1、90 s-1、120 s-1的情况下持续进行剪切试验,每次剪切都重新进行料浆配制,剪切时间持续400 s。环形剪切模式是剪切速率从0开始在120 s内均匀地增加到120 s-1,随后在120 s内剪切速率均匀减少直至为0。阶跃剪切模式是以30 s-1的剪切速率剪切30 s后,突增至60 s-1,然后再剪切30 s突增至90 s-1,再剪切30 s突增为120 s-1,最后以120 s-1的剪切速率剪切30 s。
2 试验结果与分析
2.1 不同剪切模式下剪切应力变化分析
图5为不同剪切模式下剪切应力变化规律。由图5(a)可知,在恒定剪切模式下充填尾砂料浆剪切应力随着时间逐渐降低直至趋于平缓,且在初始阶段料浆处于弹性变换阶段,不同剪切速率下其剪切应力变化速率不同,剪切速率越大其变化越慢,随后进入应力松弛阶段,剪切速率的大小对剪切应力的变化速率影响不明显,但其屈服应力在不同剪切速率下有不同的表现,剪切速率越大对絮网结构的破坏效率越小导致屈服应力越高。由图5(b)可知,环形剪切模式下剪切应力是随着时间的增加整体呈下降趋势,且前120 s与后120 s的变化规律不同,在前120 s的剪切速率上升阶段,其剪切应力变化速率逐渐降低,而后120 s的剪切速率下降阶段,剪切应力变化速率逐渐上升,与常规触变性流体不同的是,由于物料的不均匀性导致其在剪切过程中会出现小范围的剪切应力上升现象。由图5(c)可知,阶跃剪切模式下随着剪切速率的突变增加,而充填料浆并未达到此时剪切速率下的流动屈服应力所以会再次进入弹性变化阶段,随后进入应力松弛阶段,而且随着剪切速率的增加其进入应力松弛阶段时的塑性应力也会随之变大,此外,在30 s-1阶段剪切应力变化速率明显较快。由图5可知,剪切应力在不同剪切模式下是不尽相同的,在恒定剪切模式下剪切应力随着时间的增加逐渐下降,剪切速率越大,其屈服应力越大;在环形剪切模式下剪切应力无论剪切速率如何变化,其随着剪切时间的增加整体呈下降趋势;在阶跃剪切模式下剪切应力不会随着剪切速率的突变而产生突变,会再次进入弹性阶段逐渐随后进入应力松弛阶段。

图5 不同剪切模式下剪切应力变化规律
2.2 不同剪切模式下表观黏度变化分析
由图6(a)可知,在恒定剪切下充填尾砂料浆的絮网结构被破坏导致表观黏度随着时间逐渐降低,然后趋于平缓,与剪切应力变化规律大致相同,且其变化速率逐渐降低然后保持在一定程度,不同剪切速率下的最终塑性黏度有明显区别,剪切速率越大最终塑性黏度越小。由图6(b)可知,在环形剪切模式下表观黏度随着时间的增加呈指数递减,且在前30 s的低剪切速率阶段黏度变化较为显著,随着时间的推移,剪切速率逐渐降低,表观黏度逐渐恢复,与环形剪切模式下剪切应力变化规律不同,表观黏度变化在前120 s的剪切速率上升阶段与后120 s的剪切速率下降阶段曲线几乎完全对称,所以在相同的剪切速率下黏度是几乎相同的,剪切历史对其影响不明显,由此可以判断料浆触变在短时间内具有一定可逆性。由图6(c)知,在阶跃剪切模式下表观黏度在30 s-1阶段变化较快,而在60 s-1、90 s-1、120 s-1阶段变化较为缓慢,而且随着剪切速率的突增表观黏度也会随之突变,随后进入弹性变化阶段以致表观黏度会出现较短时间的上升,最后进入剪切变稀阶段,黏度逐渐降低。由图6可知,在不同剪切模式下充填尾砂料浆表观黏度变化是完全不同的,由于在剪切过程中料浆的黏度是不断变化的,所以将其趋于稳定时的黏度视为塑性黏度,恒定剪切模式下随着剪切时间的增加其表观黏度逐渐下降直至趋于稳定,且剪切速率越大,塑性黏度越小;循环剪切模式下表观黏度随着剪切时间的增加在前120 s的呈指数下降,而后120 s则与前120 s完全相反;阶跃剪切模式下表观黏度在剪切速率突增的情况下会再次进入弹性变化阶段,随后进入应力松弛阶段。

图6 不同剪切模式下黏度变化规律
2.3 拟合分析
剪切速率为60 s-1的恒定时剪切模式与阶跃剪切模式的30~60 s阶段的剪切速率是相同的,其对比可以更为清晰地看出两种不同剪切模式在相同剪切速率下触变规律的不同,而在剪切速率一定时,表观黏度与剪切应力成正比,表观黏度曲线与剪切应力曲线变化规律应是相同的,所以仅针对剪切应力曲线进行拟合分析。通过选取恒定剪切模式下剪切速率为60 s-1的30~60 s阶段和阶跃剪切模式下的30~60 s阶段的几个代表性点位进行回归分析并进行对比(图7)。

图7 回归分析图
由图8可知,由于在0~30 s阶段阶跃剪切模式的剪切速率低于恒定剪切,即使在30~60 s阶段有相同的剪切速率,但是阶跃剪切模式剪切应力低于恒定剪切模式,而且可以看出恒定剪切模式下的剪切应力直接呈现下降阶段,而阶跃模式下剪切应力有一段凸起阶段,说明在不同剪切历史下即使其剪切速率相同剪切时间相同其变化规律也会不同。

图8 剪切应力对比图
恒定剪切模式剪切应力回归方程见式(1)。
y=1 548.93×x-0.227 24
(1)
式中:y为剪切应力,Pa;x为时间,s。回归方程中决定系数R2=0.966 89,回归方程较为合适,拟合度较高。
阶跃剪切模式下剪切回归方程见式(2)。
y=465.502 78+74.553 7/(1+exp((x-53.141 77)/4.818 14))
(2)
式中:y为剪切应力,Pa;x为时间,s。回归方程中决定系数R2=0.966 63,回归方程较为合适,拟合度较高。
恒定剪切模式基本符合Allometricl模型y=a×xb,与恒定剪切模式的回归方程不同,阶跃剪切模式因为在阶跃过程中增加了弹性变化阶段,所以Allometricl模型对阶跃模式不再适用,经过优化分析发现Boltzmann模型y=A2+(A1-A2)/(1+exp((x-x0)/dx))可对其进行较好的回归,相比于Allometricl模型,Boltzmann模型增加了常数A1、A2、x0以及dx,从而对阶跃过程中产生的弹性阶段有了更好的描述,对其回归分析更为精准。
3 结 论
1) 不同剪切模式下充填尾砂料浆剪切应力变化规律明显不同,在恒定剪切模式下剪切应力逐渐下降且剪切速率越大屈服应力越大;在环形剪切模式下剪切应力无论剪切速率的增加或降低都逐步降低;在阶跃剪切模式下由于剪切速率的突变而剪切应力未达到流动的屈服应力所以剪切应力不会产生突变而是进入弹性阶段,逐渐再次进入应力松弛阶段剪切应力逐渐降低。
2) 在不同剪切模式下充填尾砂料浆表观黏度变化不同,恒定剪切模式下由于絮网结构被破坏导致其表观黏度逐渐下降直至到达该剪切速率下的破坏极限随后趋于稳定,且剪切速率越大最终塑性黏度越小;循环剪切模式下表观黏度随着剪切速率的升高其絮网结构被破坏而降低随着剪切速率的降低无法达到继续破坏絮网结构的需求所以其表观黏度逐渐升高;而阶跃剪切模式下表观黏度在剪切速率突增的情况下由于剪切应力无法达到流动所需的应力条件,所以会再次进入弹性阶段,从而黏度略微升高随后进入触变阶段黏度逐渐降低。
3) 得出了不同剪切模式下触变性的数学计算模型,在恒定剪切模式下剪切应力基本符合Allometricl模型,而阶跃模式下因为存在阶跃过程中的弹性变化阶段,所以Boltzmann模型更为精准。

