基于多重填补的广义线性模型在肾脏疾病研究中的应用

王 威 综述 杨 帆 审校

在基于临床数据的研究中,无论是回顾性还是前瞻性的研究,常常会出现数据缺失的情况。当出现了缺失值,我们应给予妥当的处理,以便做出可靠的统计推断。目前,应对缺失值的方法是多种多样的,主要有删除法和填补法。删除法又称完整案例分析(complete case analysis)或列表删除(listwise deletion),即删除存在缺失值的所有观测,对保留下来的无缺失值的观测进行统计分析。此方法的操作是最简单易行的,因此为大多数研究者所采用,也是多数统计分析软件所默认采用的方法。然而,此方法在实际运用中可能会存在两点不足:一是缺失值的存在可能不是随机的,即存在缺失值的观测与完整观测之间存在某些方面的差异,且这些差异会给后续的参数估计带来偏倚;二是在研究变量数较多的情况下,所有研究变量均无缺失的观测可能会比较少,运用此法会舍弃过多观测,不仅会严重降低投入产出比,而且会增大参数估计的标准差和置信区间,降低统计功效。只有在存在缺失值的观测占比很小的时候(比如<5%),所造成的参数估计的偏倚和统计功效的降低才可以近似忽略[1]。因此,多建议对缺失值进行填补后再进行分析。填补又称插补,可分为单一填补法和多重填补法。单一填补包括均值填补,哑变量填补和基于回归模型的单一填补等。单一填补因为会降低被填补变量的不确定性,缩小参数估计的标准差,已逐渐被淘汰,本文不作详细介绍[2]。多重填补法因其考虑了缺失的不确定性等优点越来越受到大家的推崇[3]。另外,广义线性模型(generalized linear models, GLM),囊括线性回归模型、二元Logistic回归模型、Poisson回归模型等,在临床数据分析中占据着重要地位,其中二元Logistic回归常常作为主要的多因素模型,用以产出因果推断的统计学依据[4-5]。目前,虽然二元Logistic回归与多重填补技术的结合在危险因素分析的医学研究中的应用越来越多,如Foerster等[6]通过二元logistic回归和多重填补方法建立了一个风险分层模型以更好的识别适合上尿路上皮癌内镜下保留肾脏手术的患者,但以实例分析介绍两者如何结合应用的文献较少。本文就数据缺失的模式和比例、多重填补的流程进行简单的梳理,并使用急性肾损伤的数据演示多重填补(mice程序包)与广义线性模型的结合应用,以期为含缺失值的临床数据的统计分析提供参考依据。

数据缺失的模式与比例

多重填补的创始人Little和Rubin教授将数据缺失的原因分为以下三种模式:完全随机缺失(missing completely at random, MCAR)、随机缺失(missing at random, MAR)和非随机缺失(missing not at random, MNAR)。完全随机缺失指的是数据的缺失与否既不能归因于已观测的变量,也不能归因于未观测的变量,即存在缺失的观测与完整观测来自于同一个分布的总体,完整案例分析方法仅适用于这种缺失模式[7]。但有学者认为这种缺失模式只是理论上存在的,是随机缺失的一种特殊情况[8]。随机缺失指的是数据的缺失与否取决于已观测的变量,即存在缺失的观测和完整观测的差别可以被其他观测变量解释。有研究者认为,“随机缺失”一词的命名有歧义,其 “随机”一词与“完全随机缺失”中的“随机”意义是不同的,前者是一种有条件的、可控制的缺失,更精确的表达方式为随机条件缺失(conditionally missing at random)[7-9]。非随机缺失指的是数据的缺失与否取决于未观测到的变量,即存在缺失的观测和完整观测的差别无法用所有已知变量解释。将多重填补技术应用于含有前两种缺失(即完全随机缺失和随机缺失)的数据,可得到近似无偏的参数估计结果,而非随机缺失则不在多重填补技术的应用范围。在实际应用中,事先几乎不可能知道数据的缺失究竟属于哪种类型,那么在应用多重填补法对缺失数据进行处理之时,需要先假定数据缺失符合随机缺失。只要构建填补模型时纳入足够多的变量,数据缺失的模式就会非常接近随机缺失,可以使用多重填补法进行处理[10-11]。或者可以选择多个可能适用的多重填补模型分别填补,对各个模型所得完整数据集进行相同的统计分析,将各自的结果汇总,进行敏感性分析[12]。

在应用多重填补法处理缺失数据时,数据缺失的比例对多重填补的影响目前尚存在争论[13]。人们所推荐的多重填补最多可接受的数据缺失的比例在5%～50%[14-16]。近年有学者对模拟数据进行了大量的填补运算,发现相比于数据缺失的比例,纳入填补模型的辅助变量所起的作用更加明显。即便是在缺失数据比例高达90%的情况下,只要在填补模型中纳入合适的辅助变量,填补后的数据依然可以进行无偏倚的统计推断[13]。然而此研究所填补变量均为符合正态分布的连续变量,且为模拟数据,其结论可能不适用于分类变量和其他分布类型的变量。

因此,在进行多重填补之前,应对所需填补数据的缺失值进行多方面的评估,必要时需了解各个变量收集、整理、清洗的全过程,尽可能纳入更多辅助变量进入填补模型,并使用多个填补模型,进行敏感性分析,方能尽可能减少偏倚。

多重填补的流程

以R语言程序包mice(multivariate imputation by chained equation)为例,由该程序包及相应函数实现数据多重填补的原理和过程可知 (图1),一个完整的数据多重填补过程应包括缺失值的填补和使用所得数据进行统计分析两大部分[12,17]。因此,当我们使用多重填补法对含缺失值的数据进行回归分析时,建议按照如下流程进行数据填补和回归分析:

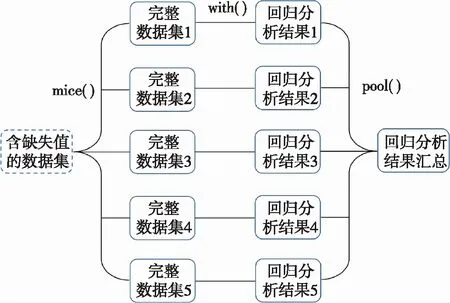
图1 基于多重填补的广义线性模型的实现流程

查看数据缺失情况当我们拿到一个数据集后,首先应当明确数据的缺失模式,即前文中提到的MCAR、MAR和 MNAR,但这一点往往难以做到。不过,我们能做的是查看数据集的缺失情况,包括明确含缺失值的变量、变量类型和缺失比例,这对是否进行填补和多重填补中一些命令行参数的设定很重要。比如,若因变量有缺失,一般我们会选择删除相应的观测行,而不对因变量进行填补;若缺失的变量既有连续变量,也有分类变量,那我们可以通过函数factor()先对分类变量进行定义,或在多重填补时为每个需要填补的变量设定正确的参数defaultMethod;若某个或某些变量的缺失比例较大(>50%),我们一般不建议进行数据填补,而建议放弃使用该变量。

缺失值的多重填补当缺失比例较低时,我们便可以采用函数mice()尝试缺失值的多重填补。在这个过程中,有3个重要的参数需要设定。第一个为参数m,用来设定多重填补生成的完整数据集的数量,默认为5。第二个为method或defaultMethod,用来指定变量的填补方法,比如pmm对应定量变量、logreg对应二分类变量、polyreg对应无序多分类变量、polr对应有序多分类变量。第三个为seed,设置种子数,使得下次再运行代码时所得到的数据集与前次一致,保证可重复性。

完整数据集的统计分析在完成数据的填补之后,我们会得到一个mids对象,该对象包含了通过链式多元填补得到的多个完整数据集。由于函数glm()中的参数data所识别的数据集类型为data frame (数据框)、list(列表)或环境 (environment),那么我们就无法直接使用函数glm()对mids对象进行回归分析。解决的方法是,联用函数with()和glm(),对mids对象中的每个数据集均进行回归分析。

统计分析结果的汇总在使用with()完成了每个数据集的回归分析后,我们会得到每个数据集对应的回归分析结果,即多套回归分析结果。接下来,我们需要使用函数pool()对多个回归分析结果进行汇总,综合为包含回归系数、标准误、P值等在内的一套回归分析结果。

在广义线性模型中的应用

案例情况如下:某肾内科医师回顾性收集了109例在院内发生急性肾损伤和231例未发生急性肾损伤患者的相关信息,包括一般特征(性别、年龄、BMI等级)和入院时的实验室检查结果(中性粒细胞和淋巴细胞比值、尿素氮、尿肌酐、尿酸、钠离子、钾离子、超敏反应蛋白、血清乳酸),拟通过二元logistic回归分析急性肾损伤的影响因素。

在广义线性模型中,将glm()函数的famliy参数设置为binomial时,所拟合的模型便是二元logistic回归模型。接下来,我们以此类回归模型为例,展示基于多重填补数据集、缺失数据集和原始数据集的广义线性模型的结果,并将基于多重填补的回归分析结果与基于无缺失值原始数据的回归分析结果进行比较(本文所用的R代码均可通过github网站查看https://github.com/hamody316/mice/blob/main/README.md#mice)。

由于本次所使用的的数据集并无缺失值,因此我们使用R程序包simFrame中的函数setNA()为性别、年龄、体质量指数(BMI)等级、尿肌酐、钠离子和血清乳酸构造了缺失值,使得他们均有5%的随机缺失。另外,在该数据集中,性别为二分类变量,BMI等级为有序多分类变量(等级变量),其他均为连续变量。

假定我们已确定了纳入到多因素回归分中的变量为性别、年龄、BMI等级、尿肌酐、钠离子和血清乳酸。在设定了填补数据集数量(m=10)、变量的填补方法和种子数后,我们得到了10个完整的数据集,使用这10个数据集进行回归分析的汇总结果如表1。

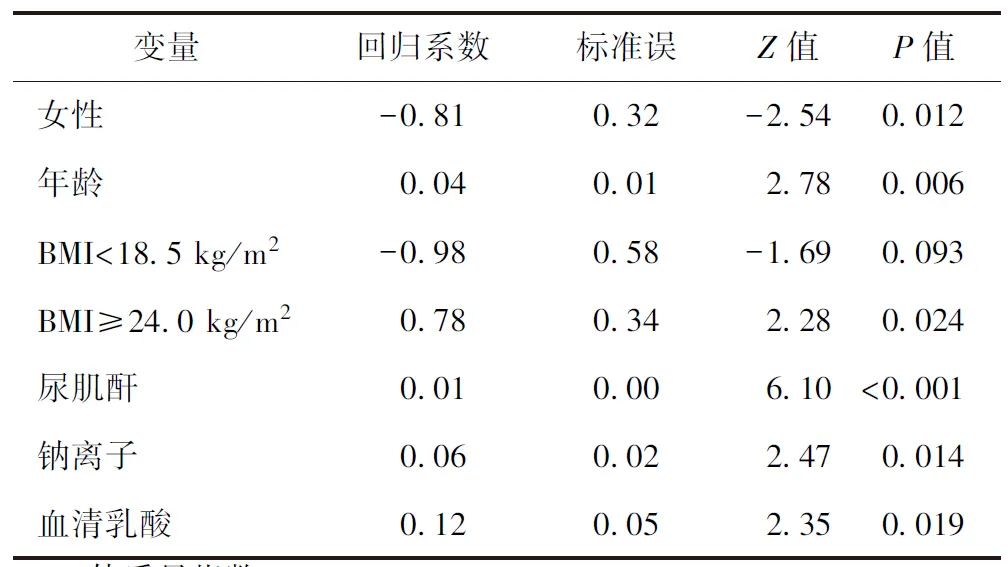
表1 基于多重填补的回归分析结果

为了能够说明多重填补的效果,我们用含缺失值的数据集和无缺失值的原始数据集分别进行了回归分析,所得结果见表2和表3;同时,我们还对表3和表1的回归系数进行了差值计算(表4)。

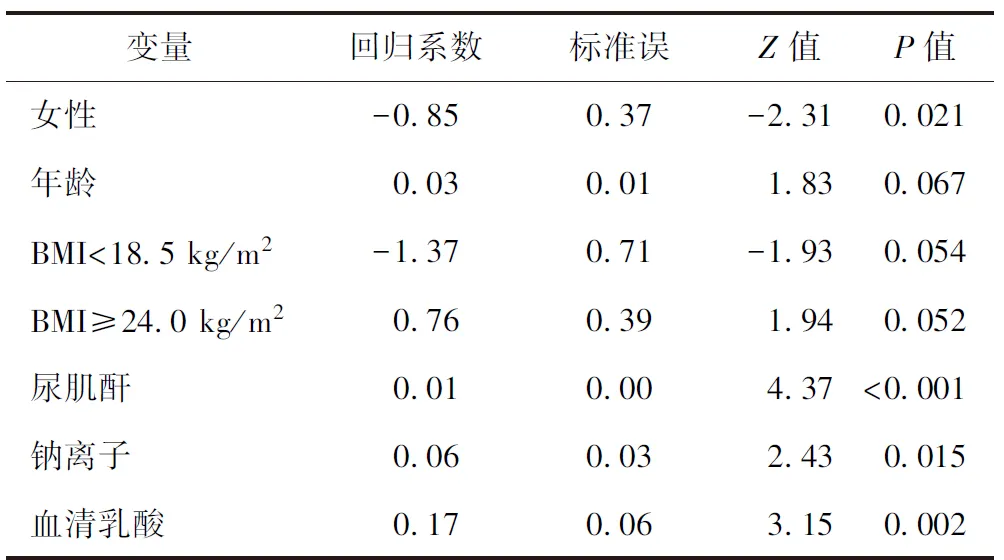
表2 基于含缺失值数据集的回归分析结果

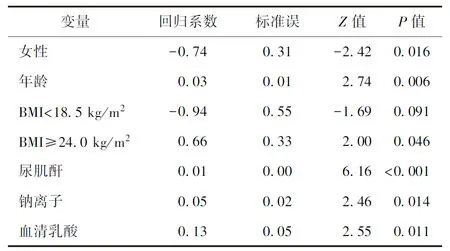
表3 基于原始数据的回归分析结果

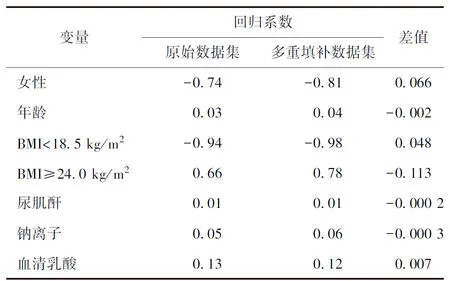
表4 回归系数的差值

由表3的结果可知,所纳入的多个变量在基于多重填补的回归分析中具有统计学意义,与急性肾损伤有统计学关联,这与表1中的结论一致。由表2的结果可知,在基于含缺失值的回归分析结果中,年龄和BMI等级与急性肾损伤无统计学关联,这与基于原始数据的回归分析的结果不一致,说明表2中的结果发生了偏倚。另外,由表4可知,基于多重填补数据得到的变量系数与基于原始数据得到的变量系数的差值很小,进一步说明多重填补得到结果的稳健性和可靠性。当然,本文多重填补的结果并不意味着多重填补对所有含缺失值的数据集而言都是最佳的填补方法,我们应该根据数据类型、缺失情况等选择合适的填补方法,比如随机森林填补法、K邻近值法等[18-19]。

小结:本文对缺失值的常见处理方法、缺失值模式、缺失值比例、多重填补的流程进行了简单总结,并通过急性肾损伤的影响因素分析的实例,展示了基于多重填补的广义线性模型的分析过程及结果。对比基于多重填补的回归分析结果、基于原始数据的回归分析结果和基于缺失数据的回归分析结果可知,在缺失比例较低时,前两者的回归分析结果(如各变量的回归系数)虽然有一定的差值,但整体结论并未出现偏倚,即在回归方程中各变量的统计学意义是一致的。这也表明,在条件适当的情况下,可以在肾病相关数据的统计分析中使用多重填补。本文结合肾病相关案例数据展示了如何使用R语言实现该方法,并对该方法所得结果的稳健性进行了验证,希望能为广大医护或科研人员在处理缺失数据的思路和实践上提供参考。