运用几何观点 探究最值问题——一道高考题的几何背景分析与推广

浙江省杭州第四中学(310002) 张 健

2019年高考数学全国III 卷第23 题以三元最值问题为载体,对学生的数学运算、逻辑推理等数学核心素养以及分析问题、解决问题的能力进行考查. 笔者运用解析几何的观点对这道高考题进行研究,发现它具有较为直观的几何背景,可以从几何角度对试题进行分析和解答,并进一步推广和改编.

一、试题呈现

题目(2019年高考全国III 卷第23 题)设x,y,z ∈R,且x+y+z=1.

(1)求(x-1)2+(y+1)2+(z+1)2的最小值;

(2)若(x-2)2+(y-1)2+(z-a)2≥成立, 证明:a≤-3 或a≥-1.

试题中的问题(1)是直接求(x-1)2+(y+1)2+(z+1)2的最小值,问题(2)可以转化为在x+y+z=1 的条件下求(x-2)2+(y-1)2+(z-a)2的最小值. 本题有多种解法,比如在问题(1)中可以将式子[(x-1)+(y+1)+(z+1)]2展开后,再运用重要不等式求解[1],这种方法需要运用构造式子的技巧,对数学能力要求较高. 我们首先运用柯西不等式解答,再对试题进行分析.

解法1(代数角度)(1)因为[(x-1)2+(y+1)2+(z+1)2](12+12+12)≥(x+y+z+1)2=4,所以(x-1)2+(y+1)2+(z+1)2≥当且仅当

(2)因为

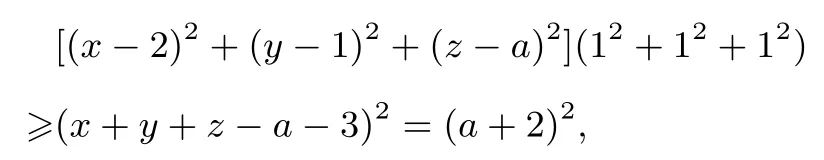
所以(x-2)2+(y-1)2+(z-a)2≥

运用代数方法解答完本题之后, 笔者产生了一个疑问:能否从几何角度对这道题进行分析和解答呢? 这引发了笔者的研究兴趣. 下面笔者尝试运用解析几何的观点对试题进行分析,探究试题的几何背景.

二、几何背景

作为分析试题的基础,首先将空间解析几何中有关结果叙述如下[2](以下结果约定在空间直角坐标系O-xyz中):

1 平面的方程

(1) 平面的点法式方程: 方程A(x - x0) +B(y -y0) +C(z - z0) = 0 (A2+B2+C2/= 0) 表示过点M(x0,y0,z0) 且垂直于向量n= (A,B,C) 的平面(如图1),其中n=(A,B,C)称为该平面的法向量.

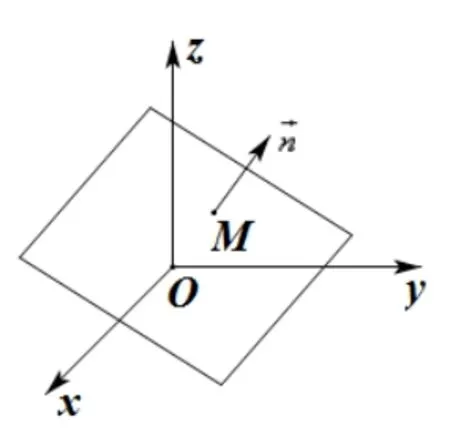
图1

图2

(3) 平面的一般方程: 方程Ax+By+Cz+D=0 (A2+B2+C2/= 0) 表示一个平面(如图3), 该平面的一个法向量为n=(A,B,C).

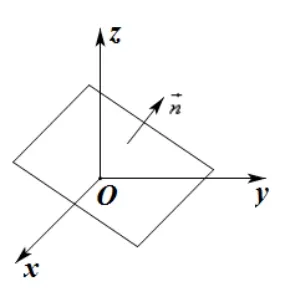
图3

2 两点间的距离

设A(x1,y1,z1),B(x2,y2,z2), 则A,B两点间的距离|AB|=

3 点到平面的距离

(1) 设平面A(x - x0) +B(y - y0) +C(z - z0) =0(A2+B2+C2/= 0), 则平面外一点P(a,b,c) 到该平面的距离d=(如图4).

图4

(2) 设平面Ax+By+Cz+D= 0 (A2+B2+C2/= 0), 则平面外一点P(a,b,c) 到该平面的距离d=

根据以上结果, 试题中的条件x+y+z= 1 可以表示一个平面. 由此, 从解析几何的角度来看, 问题(1) 中的(x-1)2+(y+1)2+(z+1)2表示点P(1,-1,-1)与平面x+y+z=1 上的动点Q(x,y,z)之间的距离|PQ|的平方,即|PQ|2. 而问题(2)中的(x-2)2+(y-1)2+(z-a)2表示点P′(2,1,a)与平面x+y+z=1 上的动点Q(x,y,z)之间的距离|P′Q|的平方,即|P′Q|2.

因此,试题的问题(1)和(2)可以分别转化为下面两个问题:

(1′) 如图5, 已知点P(1,-1,-1), 设Q(x,y,z) 是平面x+y+z=1 上任意一点,求|PQ|2的最小值.

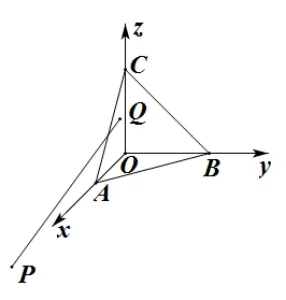
图5

(2′) 如图6,已知点P′(2,1,a), 设Q(x,y,z)是平面x+y+z=1 上任意一点,求|P′Q|2的最小值.

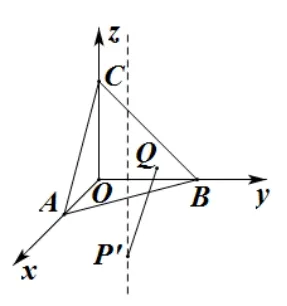
图6

问题(1′) 只要运用点到平面的距离公式求出点P(1,-1,-1) 到平面x+y+z= 1 的距离d, 即为|PQ|的最小值,从而可求得|PQ|2的最小值. 问题(2′)方法相同.由此,我们从几何角度给出一种新的解法:

解法2(几何角度)

(1)如图5,设平面x+y+z=1 上任意一点为Q(x,y,z),记点P(1,-1,-1),则|PQ|2=(x-1)2+(y+1)2+(z+1)2.由1-1-1/=1,可得点P(1,-1,-1)在平面x+y+z=1 外.平面x+y+z=1 即x+y+z-1=0,因此点P(1,-1,-1)到平面x+y+z= 1 的距离d=所以(x-1)2+(y+1)2+(z+1)2的最小值为

(2)如图6,设平面x+y+z=1 上任意一点为Q(x,y,z),记点P′(2,1,a),则|P′Q|2=(x-2)2+(y-1)2+(z-a)2.

当a=-2 时,由2+1+a=1,可得点P′(2,1,a)在平面x+y+z= 1 上. 当x= 2,y= 1,z=a时,P′和Q重合,即|P′Q|= 0,此时(x-2)2+(y-1)2+(z-a)2取到最小值0,不符合题意.

当a /=-2 时,由2 + 1 +a /= 1, 可得点P′(2,1,a)在平面x+y+z= 1 外,因此点P′(2,1,a) 到平面x+y+z= 1 的距离d=所以(x-2)2+(y-1)2+(z-a)2的最小值为由解得a≤-3 或a≥-1.

三、结论推广

在解法2 中,我们把试题中的条件x+y+z=1 理解为平面的方程,结合不同形式的平面方程,我们可以将问题的结论进行推广.

推论1设x,y,z ∈R,且Ax+By+Cz+D=0(A2+B2+C2/=0),则f(x,y,z)=(x-a)2+(y-b)2+(z-c)2的最小值fmin(x,y,z)=

证明设平面Ax+By+Cz+D= 0 (A2+B2+C2/= 0) 上任意一点为Q(x,y,z), 记点P(a,b,c), 则|PQ|2=f(x,y,z) = (x-a)2+ (y-b)2+ (z-c)2. 当aA+bB+cC+D= 0 时,点P(a,b,c) 在平面上. 当P与Q重合时, 可得fmin(x,y,z) == 0. 当aA+bB+cC+D /= 0 时,点P(a,b,c) 不在平面上,P与Q的最短距离|PQ|min=d=所以

综上所述,fmin(x,y,z)=

将推论1 中的条件Ax+By+Cz+D=0(A2+B2+C2/= 0)特殊化为A(x-x0)+B(y -y0)+C(z -z0) =0(A2+B2+C2/=0)便可以得到以下推论2:

推论2设x,y,z ∈R, 且A(x - x0) +B(y - y0) +C(z - z0) = 0(A2+B2+C2/= 0), 则f(x,y,z) =(x-a)2+ (y-b)2+ (z-c)2的最小值fmin(x,y,z) =

将推论1 中的条件Ax+By+Cz+D=0(A2+B2+C2/= 0)特殊化为= 1 (pqr /= 0)便可以得到以下推论3:

推论3设x,y,z ∈R, 且= 1 (pqr /= 0),则f(x,y,z) = (x-a)2+ (y-b)2+ (z-c)2的最小值fmin(x,y,z)=

进一步可将推论1 推广到多个变量的情形:

推论4设x1,x2,··· ,xn ∈R,且a1x1+a2x2+···+anxn+b=0(a21+a22+···+a2n /=0),则f(x1,x2,··· ,xn)=(x1-m1)2+(x2-m2)2+···+(xn-mn)2的最小值fmin(x1,x2,··· ,xn)=

注该推论的几何背景即n维欧式空间Rn中的欧氏距离

我们运用柯西不等式进行证明.

证 明当a1m1+a2m2+···+anmn+b= 0时, (x1,x2,··· ,xn) = (m1,m2,··· ,mn) 是 方 程a1x1+a2x2+···+anxn+b= 0 的解. 由f(x1,x2,··· ,xn) ≥f(m1,m2,··· ,mn)=0,得fmin(x1,x2,··· ,xn)=0.

当a1m1+a2m2+···+anmn+b/=0 时,由柯西不等式,得

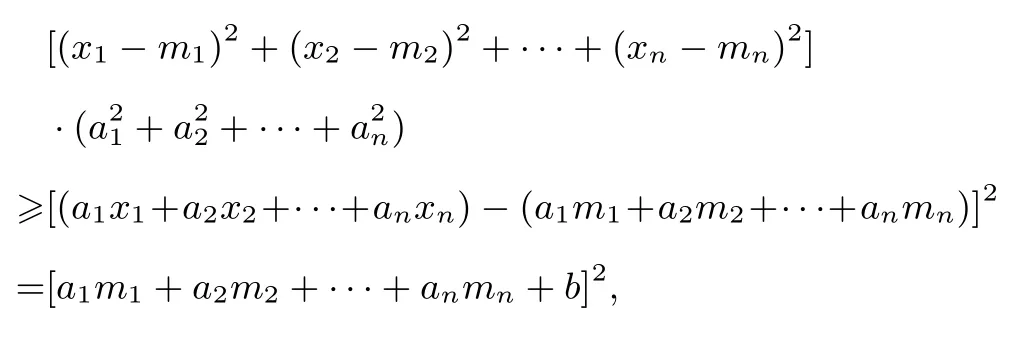
又a21+a22+···+a2n /=0,所以

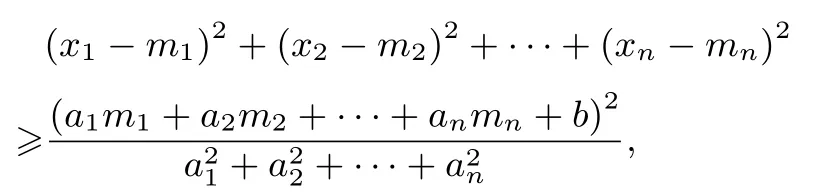
当且仅当

时等号成立,其中λ ∈R,即

所以

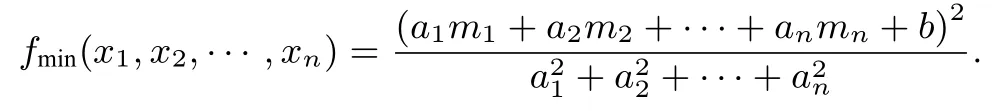
综上所述,命题成立.

四、试题改编

借助试题的几何背景和以上推论,我们可以对题目进行改编.

1 等式条件改为不等式条件

改编1设x,y,z ∈R,且x+y+z≤1,求(x-1)2+(y+1)2+(z+1)2的最小值. (答案: 0.)

分析x+y+z≤1 表示平面x+y+z= 1 包含原点的一侧区域(含平面),点P(1,-1,-1)在x+y+z≤1 表示的区域内. 所以当区域x+y+z≤1 内的动点Q(x,y,z)与P(1,-1,-1)重合时,(x-1)2+(y+1)2+(z+1)2取到最小值0.

改编2设x,y,z ∈R,且x+y+z≥1,求(x-1)2+(y+1)2+(z+1)2的最小值. (答案:

分析x+y+z≥1 表示平面x+y+z= 1 不包含原点的一侧区域(含平面),点P(1,-1,-1)不在x+y+z≥1表示的区域内. 当区域x+y+z≥1 内的动点Q(x,y,z)与P(1,-1,-1) 在平面上的投影点重合时,P与Q的距离最短, 此时(x -1)2+(y+1)2+(z+1)2取到最小值,所以只要求出点P(1,-1,-1) 到平面x+y+z= 1 的距离即可, 问题就转化为试题的问题(1), 解法2 已求出(x-1)2+(y+1)2+(z+1)2的最小值为

2 参数特殊化

将推论1 中的参数取特殊值, 令A= 1,B= 2,C=2,D=-6,a=b=c=0,便可以改编得到如下高考题:

改编3(2018年江苏卷第24 题) 若x,y,z为实数, 且x+2y+2z=6,求x2+y2+z2的最小值. (答案: 4.)

分析根据推论1 可以直接得到答案,也可以运用柯西不等式(x2+y2+z2)(12+22+22)≥(x+2y+2z)2解答.

如果改变变量的个数,可以进一步改编如下:

3 三元情形变成二元情形

改编4若x,y为实数,且x+2y= 6,求x2+y2的最小值. (答案:.)

分析本题的几何背景即求原点到直线x+2y= 6 的距离d=的平方,可求得x2+y2的最小值为也可以运用柯西不等式(x2+y2)(12+22) ≥(x+2y)2解答.

4 三元情形推广到多元情形

改编5若x1,x2,x3,x4∈R,且x1+x2+x3+x4=0,求x21+x22+x23+x24-2x2+1 的最小值. (答案:

分析f(x1,x2,x3,x4)=x21+x22+x23+x24-2x2+1=x21+(x2-1)2+x23+x24,根据推论4,fmin(x1,x2,x3,x4)=本题还可以运用柯西不等式解答.

数学家华罗庚先生曾经说过,“数缺形时少直觉,形少数时难入微”[3],本文运用解析几何的观点对高考题的探究过程体现了数形结合思想的运用. 通过几何的视角,我们可以更加直观地认识代数问题的几何背景,挖掘代数符号背后的数学本质.

在教学实践和研究的过程中,不妨从代数、几何等多个角度看待数学问题,解释数学概念,分析数学问题,探究数学本质[4],加深对数学问题的理解.