2021年全国新高考Ⅰ卷立体几何解答题的解法探究与备考建议

广东省湛江一中培才学校(524037) 魏 欣

立体几何解答题历年来是考生抢分的“必争之题”. 2021年全国新高考Ⅰ卷立体几何解答题,延续了近几年的命题风格,充分体现了对立体几何基础知识、基本技能、基本思想和基本活动经验的考查. 试题注重基础,立足教材,难度适中,该题以三棱锥为载体,考查直线与直线、直线与平面、平面与平面的位置关系,综合考查空间想象能力、推理论证能力和运算求解能力,注重考查数学抽象、逻辑推理、直观想象和数学运算等素养,体现在直观感知、操作确认、推理论证、度量计算等方法上,着重考查点、线、面位置关系的判断与证明,以及空间角、体积的计算问题.

一、试题展示与评析

题目(2021年全国新高考Ⅰ卷第20 题) 如图1, 在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.

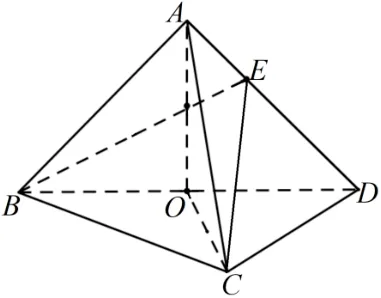
图1

(1)证明:OA⊥CD;

(2)若ΔOCD是边长为1 的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC -D的大小为45°,求三棱锥A-BCD的体积.

试题分析此题以三棱锥为载体考查直线与直线垂直、直线与平面垂直、平面与平面垂直的位置关系, 二面角, 体积等基础知识. 其中,第(2)问表面上看,似乎是考查三棱锥的体积问题,实际上其考查重点为二面角问题. 只有通过条件“二面角E -BC -D的大小为45°”才能求得“三角形ABD的高OA的长度”,从而求解“三棱锥A-BCD的体积”. 此题可采用“空间向量”这一有力的工具进行求解: 先建立空间直角坐标系,假设“OA的长度为h”,从而得到所需要的点、向量的坐标,再求解两个半平面的法向量,并求两个法向量夹角的余弦值, 由于该余弦值的绝对值等于通过方程可以求得h的值. 当OA的长度求出后,求解三棱锥A-BCD的体积就显而易见了. 此题也可以采用“几何法”进行求解,“几何法”一般按照“一作、二证、三指、四求、五答”的步骤进行.

二、解法探究

(1)证明在ΔABD中,因为AB=AD,O为BD中点, 所以AO⊥BD. 因为平面ABD⊥平面BCD, 且平面ABD∩平面BCD=BD,AO ⊂平面ABD,因此AO⊥平面BCD. 因为CD ⊂平面BCD,所以AO⊥CD.

(2)解答

解法1(法向量法)由题设得ΔBCD为直角三角形,且BC⊥CD,CD=OB=OD=OC=1,则BC=以O为坐标原点,OD为y轴,OA为z轴,垂直OD且过O的直线为x轴,建立如图2 所示的空间直角坐标系O-xyz.

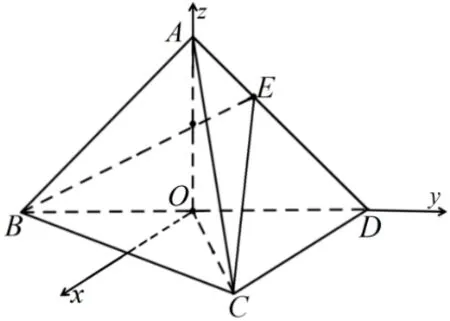
图2

设A(0,0,h)(h ＞0), 则B(0,-1,0),D(0,1,0),所 以=设平面BCE法向量为n=(x,y,z), 则故令y=-h, 则x=z= 2, 所以取平面BCD法向量为m=(0,0,1),又因为二面角E-BC-D的大小为45°,

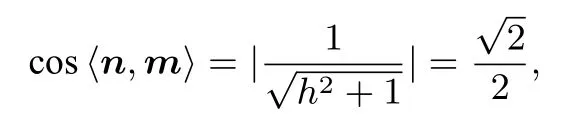
解得h= 1, 所以OA= 1, 所以故三棱锥A-BCD的体积为

小结用向量法求平面与平面所成的二面角的步骤:

①建系设点: 建立合理的坐标系,写出相关点的坐标;

②求相关向量: 求出两个平面的法向量;

③求向量的夹角: 求出两个法向量的夹角;

④转化: 将向量夹角的余弦值转化为二面角的余弦值;

⑤答: 点明平面和平面所成二面角的平面角的值.

解法2(利用二面角的定义) 如图3 所示, 过点E作EF//OA, 交BD于点F. 过点F作FG//CD交BC于点G, 连结EG.并建立空间直角坐标系O - xyz. 设A(0,0,h), 则B(0,-1,0),设G(xG,yG,0),(xG,yG+1,0),

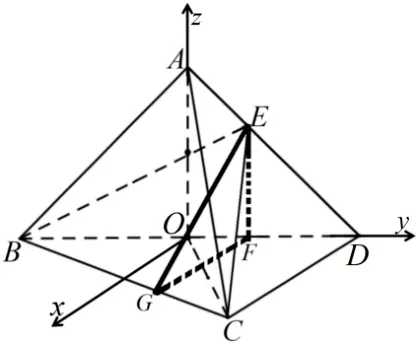
图3

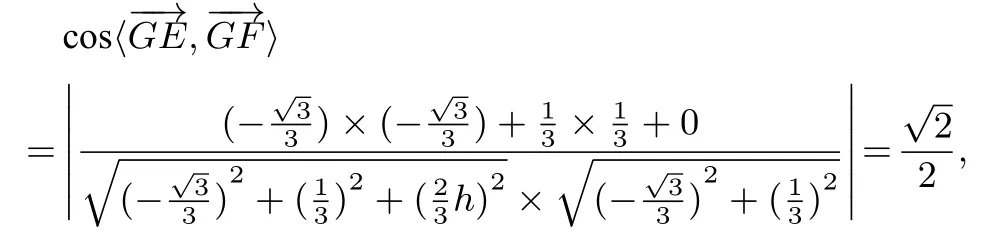
解得h=1,以下同解法1.

小结利用二面角的定义求解二面角方法: 如图4,A,C分别是二面角α-l-β的棱l上两点, 点B,D分别在半平面α,β内,且AB⊥l,CD⊥l,则与所成的角就是二面角的平面角. 即在棱上取两点(也可重合),以这两点为起点分别在两个半平面内作与棱垂直的向量,或分别过两个半平面内的点(作为所作向量的起点)作与棱垂直的向量,则这两个向量所成的角就是二面角的平面角.

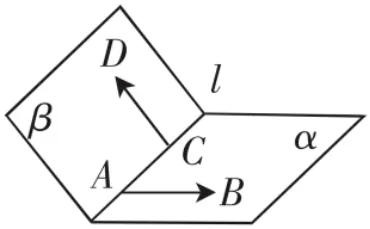
图4

解法3(构造长方体法)如图5所示,构造长、宽、高分别为的长方体, 并建立空间直角坐标系O′ -xyz. 则B(1,0,0),所以=设平面BCE法向量为n=(x,y,z),则

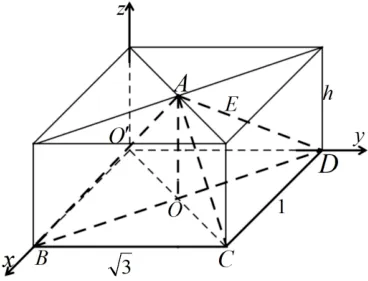
图5

令z= 1,所以x=h,y= 0,所以平面BCE法向量为n=(h,0,1),以下同解法1.

归类向量法采用空间向量解立体几何问题的关键是合理建立坐标系,选择坐标系的原则就是将底面顶点尽可能多的置于坐标轴上,这样能确保正确读取空间点的坐标. 下面给出法向量法的各种坐标系下相关向量的坐标.

坐标系坐标向量--→BE --→CE 平面BCE的法向量n images/BZ_7_1319_2011_1621_2226.png(0, 4 3, 2 3h)(-3 2 ,-1 6, 2 3h)(3h,-h,2)images/BZ_7_1319_2284_1621_2529.pngimages/BZ_7_1319_2581_1621_2808.pngimages/BZ_7_1319_2861_1622_3105.png(2 3, 23 3 , 2 3h)(-5 6,3 6 , 2 3h)(h,-3h,2)

images/BZ_8_277_325_542_564.pngimages/BZ_8_277_612_542_832.png(-2 3, 23 3 , 2 3h)(-2 3,-3 3 , 2 3h)(h,0,1)images/BZ_8_277_889_542_1105.pngimages/BZ_8_277_1163_542_1382.pngimages/BZ_8_277_1459_542_1639.png(2 3,-23 3 , 2 3h)(2 3,3 3 , 2 3h)(-h,0,1)images/BZ_8_277_1720_542_1930.png(23 3 , 2 3, 2 3h)(-3 3 , 2 3, 2 3h)(0,-h,1)images/BZ_8_277_2002_543_2202.png(-2 3, 23 3 , 2 3h)(-2 3,-3 3 , 2 3h)(h,0,1)images/BZ_8_277_2298_542_2458.png(0, 4 3, 2 3h)(-3 2 ,-1 6, 2 3h)(3h,-h,2)images/BZ_8_277_2559_544_2750.png(-4 3,0, 2 3h)(1 6,-3 2 , 2 3h)(h,3h,2)

解法4(几何法)

如图6 所示, 过点E作EF//OA, 交BD于点F. 过点F作FG//CD交BC于点G, 连结EG. 由(1) 知OA⊥平 面BCD, 又EF//OA, 则EF⊥平面BCD. 依题知在ΔBCD中,CD=OB=OD=OC= 1, 则∠BCD=90°, 即CD⊥BC. 从而FG⊥BC, 所以∠EGF是二面角E - BC - D的平面角, 即∠EGF= 45°, 则ΔEGF是等腰直角三角形. 又因为DE= 2EA, 所以FD= 2OF,则从而EF=FG=则有OA== 1, 又故三棱锥A-BCD的体积为VA-BCD=

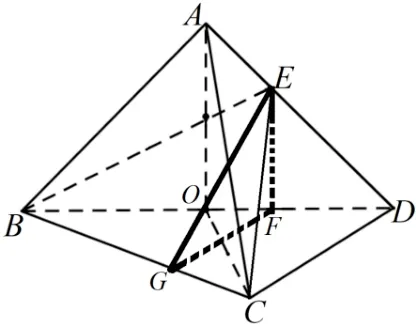
图6

小结基于二面角的平面角概念,可利用三垂线定理及逆定理作出二面角的平面角,如图7,在二面角α-l-β中,在平面β内取一点B, 过点B作平面α的垂线, 垂足为点A,过点A作AO⊥l于点O,连接BO,因为AB ∩AO=A,AB,AO ⊂平面AOB,所以l⊥平面AOB,所以l⊥OB,所以∠AOB为二面角α-l-β的平面角;若二面角α-l-β的平面角为钝二面角,如图8,则取∠AOB的补角.

图7

图8

用几何法求直线与平面所成的角的步骤:

①一作——从交线上一点出发在两平面内作出(或找出)交线的垂线;

②二证——论证作出(或找出)的线与交线同时垂直;

③三指——指出所求的二面角的平面角是哪个角;

④四求——在三角形中求角;

⑤五答——点明平面和平面所成二面角的平面角的值.

下面总结各种几何法的主要计算量,如下表:

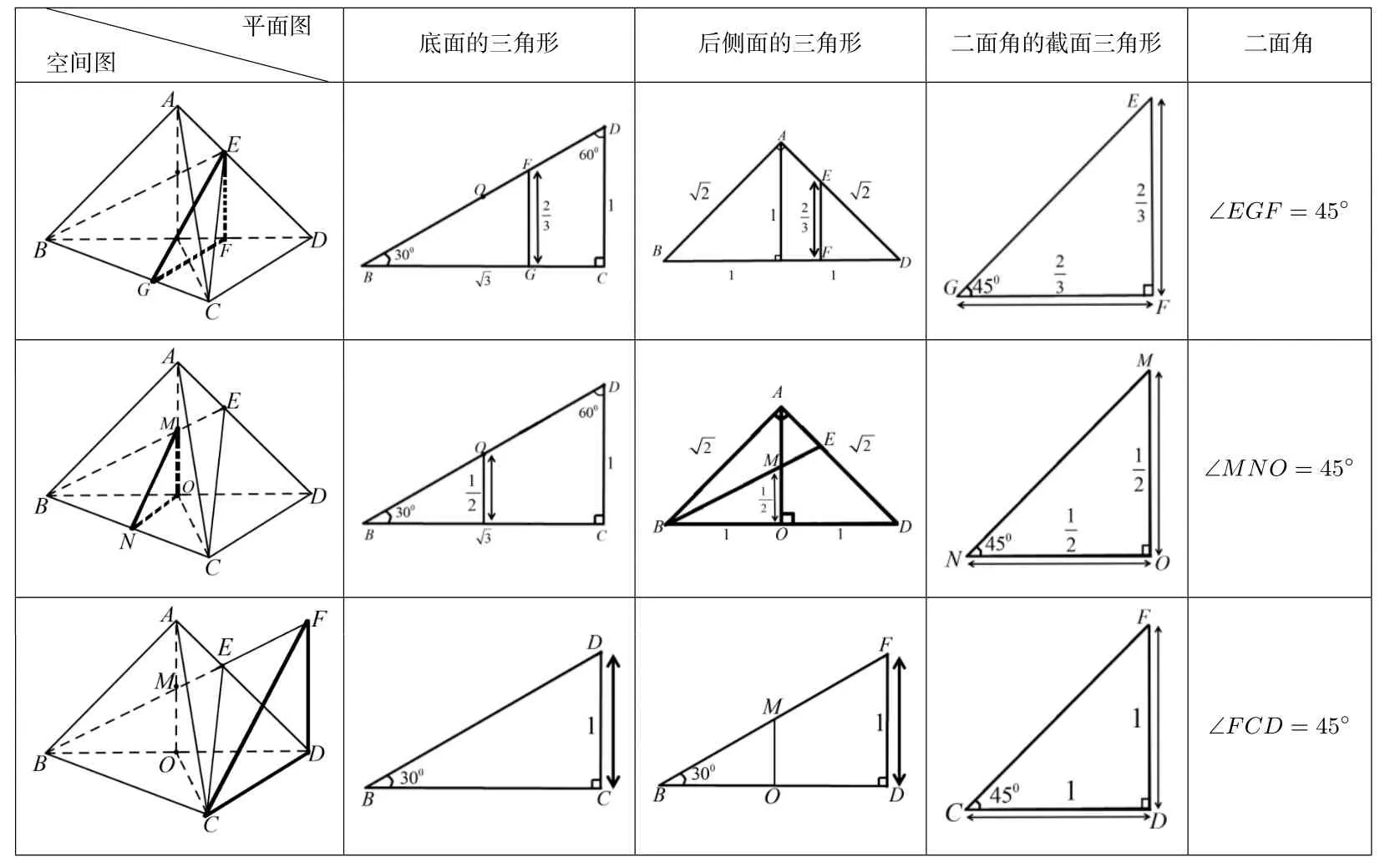
空间图平面图底面的三角形后侧面的三角形二面角的截面三角形二面角images/BZ_9_460_412_816_691.pngimages/BZ_9_853_452_1166_651.pngimages/BZ_9_1201_460_1514_643.pngimages/BZ_9_1550_416_1828_685.png∠EGF =45°images/BZ_9_460_721_814_998.pngimages/BZ_9_853_761_1166_959.pngimages/BZ_9_1201_767_1515_953.pngimages/BZ_9_1550_728_1825_991.png∠MNO =45°images/BZ_9_460_1029_816_1306.pngimages/BZ_9_853_1063_1166_1274.pngimages/BZ_9_1202_1066_1512_1270.pngimages/BZ_9_1550_1033_1827_1302.png∠FCD =45°

综观近几年高考中立体几何的解答题,对垂直的考查较多, 对垂直的直接考查或者对与垂直相关知识的间接考查,高考命题中为了兼顾两方面,常常出于建立空间坐标系的考虑,试题中都有意设计垂直的条件或垂直的结论,垂直为各种元素(角、距离、面积、体积)的量化提供了可能. 平面几何性质的渗透,解三角形工具的应用,为度量各种元素的计算公式提供强大的支撑. 可以说,垂直的知识容量大,关联元素多,发散空间广,在客观上是处于核心地位的,在立体几何中,可谓处处有垂直,下面的图9 反映了垂直与方方面面的联系.

图9

对线面垂直的复习,要做到不惜时,不怕重复;能够引导学生熟练地论证线线垂直⇄线面垂直⇄面面垂直的双向转化. 加强“垂直的等价转换”的训练. 高考常考的立体几何中特殊图形的垂直问题如下面表格.

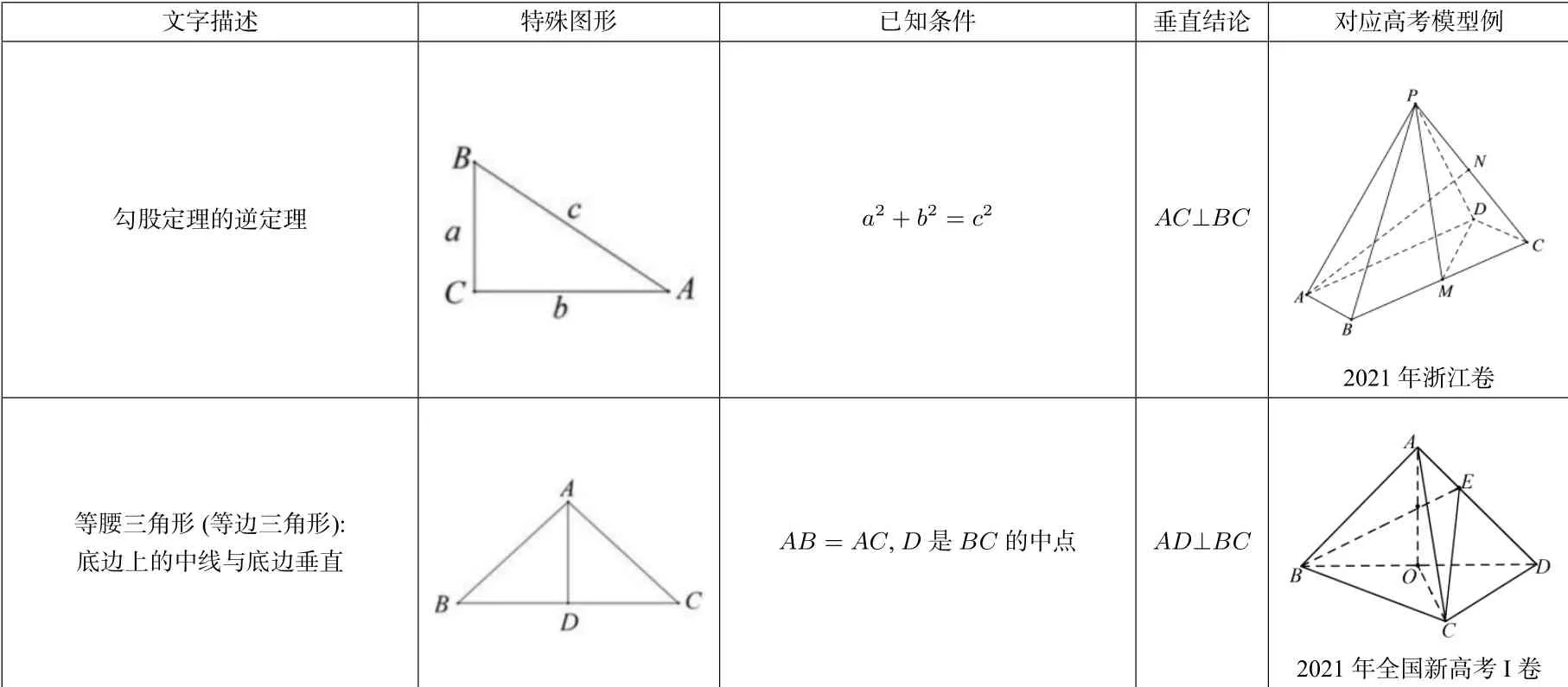
文字描述特殊图形已知条件垂直结论对应高考模型例勾股定理的逆定理images/BZ_9_855_2301_1150_2506.pnga2+b2 =c2 AC⊥BC images/BZ_9_1830_2225_2142_2539.png2021年浙江卷等腰三角形(等边三角形):底边上的中线与底边垂直images/BZ_9_846_2688_1159_2872.pngAB =AC,D 是BC 的中点AD⊥BC images/BZ_9_1834_2638_2138_2875.png2021年全国新高考Ⅰ卷

圆: 直径所对的圆周角为90°images/BZ_10_716_385_1029_656.pngAB 是圆O 的直径AC⊥BC images/BZ_10_1808_359_2094_640.png2020年全国Ⅰ卷正方形、长方形(矩形)images/BZ_10_738_780_1005_1018.png四边形ABCD 是正方形AB⊥BC BC⊥CD CD⊥AD AB⊥AD AC⊥BD images/BZ_10_1799_738_2101_1015.png2021年北京卷images/BZ_10_752_1141_995_1409.png四边形ABCD 是长方形(矩形)AB⊥BC BC⊥CD CD⊥AD AB⊥AD images/BZ_10_1830_1111_2071_1394.png2021年上海卷images/BZ_10_739_1533_1008_1826.png正方形ABCD 中,M,N 分别为DC,BC 的中点AN⊥BM images/BZ_10_1812_1491_2088_1821.png2017年北京卷菱形images/BZ_10_694_1966_1049_2153.png四边形ABCD 是菱形AC⊥BD images/BZ_10_1772_1923_2127_2155.png2013年陕西理科卷images/BZ_10_694_2275_1052_2512.png四边形ABCD 是菱形,且∠DAB =60°,E,F分别是AB,BC 的中点.AC⊥BD DE⊥AB DE⊥DC DF⊥BC DF⊥AD images/BZ_10_1750_2254_2151_2489.png2018年北京卷梯形images/BZ_10_694_2603_1052_2797.png四边形ABCD 是等腰梯形,AB//DC且AD =DC =BC =a,AB =2a.AC⊥BC AD⊥BD images/BZ_10_1799_2589_2103_2768.png2011年江西理科卷images/BZ_10_694_2916_1052_3129.png四边形ABCD 是直角梯形,AB//DC,∠ADC =90°,AD =DC =a,AB =2a,E 是AB 中点.AC⊥BC CE⊥AB images/BZ_10_1799_2869_2100_3136.png2012年广东文科卷

判定定理A PD⊥DA,PD⊥DC,DA ∩DC =D DA,DC ⊂平面ABCD PD⊥平面ABCD images/BZ_11_1752_357_2019_689.png2021年全国甲卷理判定定理B images/BZ_11_646_804_1004_1099.png平面PAD⊥平面ABCD,平面PAD∩平面ABCD =AD,AB⊥AD,AB ⊂平面ABCD AB⊥面ADP images/BZ_11_1735_787_2037_1072.png2021年新高考II 卷判定定理C PD⊥平面ABCD,PD ⊂平面PAD 平面PAD⊥平面ABCD images/BZ_11_1735_1169_2036_1492.png2021年全国乙卷理

注以上表格中,判定定理A:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直. 性质定理B:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直. 判定定理C:一个平面过另一个平面的垂线,则这两个平面垂直.

三、教材寻根

高考题的命题有些是来源于教材, 但往往又高于教材,因而我们的课堂教学需要回归教材,扎根教材,根深才能叶茂,源远方能流长. 新人教A 版《普通高中教科书·数学(必修)》第二册第143 页习题的第7 题,也出现在旧人教A 版《普通高中课程标准实验教科书·数学(必修2)》选修2-1的第三章第3 节第109 页例4,在其他版本的教材中也同样是经典例、习题,题目如下:

典例1如图10 所示, 在四棱锥P-ABCD中, 底面ABCD是正方形, 侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,过点E作EF⊥PB于点F. 求证:

图10

(1)PA//平面EDB; (2)PB⊥平面EFD; (3)求二面角C-PB-D的大小.

证明以D为坐标原点, 射线DA,DC,DP分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系D-xyz.

(1) 如图11 所示. 依题意得A(1,0,0),P(0,0,1),连接AC与BD相交于点G, 从而且=所以即PA//EG. 而EG ⊂平面EDB,且PA /⊂平面EDB,因此PA//平面EDB.

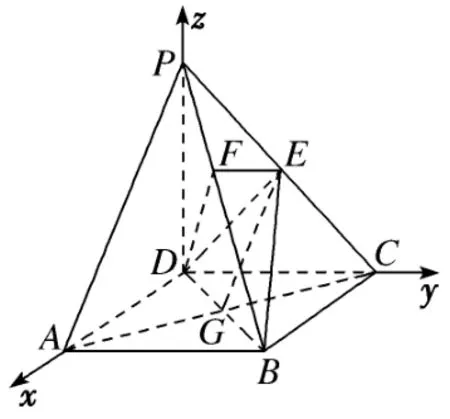
图11

(2)依题意得B(1,1,0),即PB⊥DE. 由已知EF⊥PB,且EF ∩DE=E,所以PB⊥平面EFD.

(3)证法一(向量法): 已知EF⊥PB, 由(2) 可知DF⊥PB, 故∠EFD是二面角C - PB - D的平面角.设F(x,y,z), 则= (x,y,z -1). 因为得x=k,y=k,z= 1- k. 因为= 0, 得所以所以由cos ∠EFD=所以∠EFD= 60°, 即二面角C-PB-D的大小为

(3)证法二(几何法): 由已知条件知PB⊥EF,又由第二问知PB⊥DF,所以∠EFD是二面角C-PB-D的平面角.设DC=PD=1,所以PC=又由E为PC的中点,所以EC=所以DE=又因为PC=所以由等面积法得PD·DB=PB·DF,所以DF=

又 因 在RtΔPBC中, tan ∠BPC=所以sin ∠BPC=所 以EF=PE ·sin ∠BPC=所以

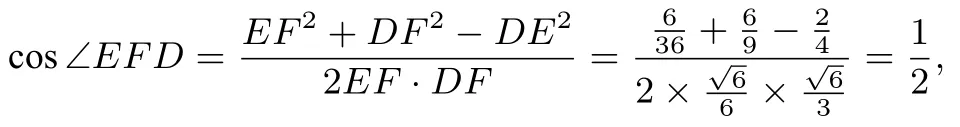
所以∠EFD=所以二面角C-PB-D的大小为

四、真题回顾

由剖析不难发现, 以上教材题目、2021年全国新高考Ⅰ卷第20 题、2014年新课标全国Ⅱ卷理科第18 题、2019年北京理科第16 题,相似度很高,可以看成是同类问题,注意回归教材,将教材内容吃透,将教材的典型例题和习题进行深入研究, 注重在教材例题与习题的基础之上合理拓展变式,赋予教材内容以灵魂和活力;研究教材不是为了押题,更不是为了寻求所谓的“秒杀技”,只是为了能够更好的领悟教材编写者的意图,弄清问题本质,寻求解决问题的一般方法,以期能够以不变应万变,真正意义上提升数学素养.

例1(2014年高考新课标Ⅱ卷理科第18 题)如图12,四棱锥P - ABCD中, 底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

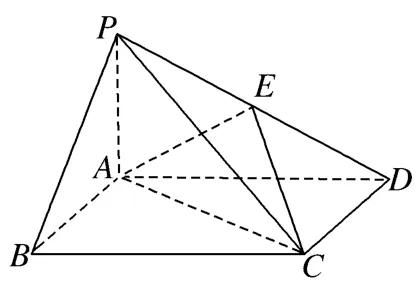
图12

(1)证明:PB//平面AEC;

(2)设二面角D-AE-C为60°,AP=1,AD=3,求三棱锥E-ACD的体积.

例2(2019年高考北京卷理科第16 题)如图13,在四棱锥P -ABCD中,PA⊥平面ABCD,AD⊥CD,AD//BC,PA=AD=CD= 2,BC= 3.E为PD的中点,点F在PC上,且

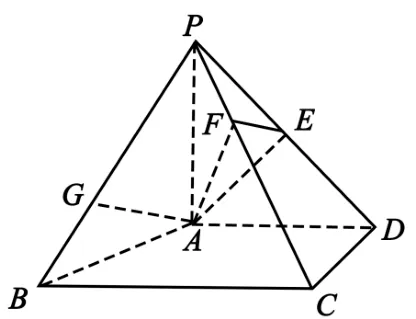
图13

(1)求证:CD⊥平面PAD;

(2)求二面角F -AE-P的余弦值;

(3)设点G在PB上,且判断直线AG是否在平面AEF内,说明理由.

五、备考建议

根据解法探究和图形归类,总结出求解立体几何解答题的模型和套路,如下图14,在教学实践中要引导学生着眼于图形探究,从而形成解决此类问题的模式和套路.

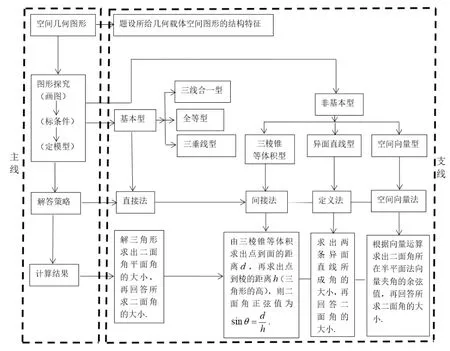
图14

历年高考立体几何的解答题常以棱锥或棱柱为载体,考查内容均较为稳定,均考查立体几何的基本知识和基本思想方法,考查空间中直线与直线、直线与平面、平面与平面的位置关系, 线、面角问题, 面积、体积等问题. 一般采用分步设问的方式,常见的两个考查热点: 一是定性分析,主要是以平行、垂直的证明为主;二是定量分析,主要考查表面积、体积的计算,线面角、二面角和距离的计算等.

解题时,平行、垂直这两种位置关系的证明一般以考纲要求的判定定理、性质定理为基本依据进行演绎推理;表面积、体积的计算常需进行合理的等积变换、割补转化,并结合表面积、体积公式进行运算;线面角、二面角的求解常运用空间向量的方法和几何法进行求解. 解答题的解题方法往往不唯一,常有多种解法,倡导学生多角度地思考与分析问题,根据图14 给出的模式和套路,从中探寻合理、简捷的途径.