基于粒子群优化算法-广义回归神经网络的磷化膜耐蚀性预测模型
姚 宏,于七龙,那 琳*
(1.河北建材职业技术学院,河北秦皇岛066004;2.东北大学秦皇岛分校,河北秦皇岛066004)
磷化是在金属表面发生化学和电化学反应生成一层磷化膜的过程,磷化膜能有效抑制金属腐蚀,起到良好的防护作用。然而,磷化过程涉及多个工艺参数,比如磷化液温度、磷化时间等,这些工艺参数都会影响磷化膜耐蚀性。如果通过实验来测试,不仅工作量繁重,而且容易混乱和出错。神经网络具有较强的自组织学习能力和非线性映射能力[1-4],借助于神经网络可以建立工艺参数与磷化膜耐蚀性之间的映射关系,并根据获得的样本数据对磷化膜耐蚀性进行预测。
目前已经应用的神经网络主要有误差逆向传播的前馈型神经网络(BPNN)[5]、广义回归神经网络(GRNN)[6]、径向基神经网络(RBFNN)[7]、循环神经网络(RNN)[8]和线性神经网络(LNN)[9]等,它们都有优势和局限性。其中,广义回归神经网络在学习速度和逼近能力等方面具有优势,另外还具有较强的非线性映射能力,即使样本数据较少的情况下也能获得良好的预测结果,因此受到青睐。但是在磷化膜耐蚀性预测方面,目前相关报道很少。从神经网络实际应用的角度考虑,有必要继续开展这方面研究。鉴于GRNN具有突出的性能优势,笔者引入GRNN建立磷化膜耐蚀性预测模型,并采用不同算法优化预测模型。
1 实验
1.1 磷化膜制备
采用浸渍磷化法在45钢表面制备磷化膜,具体流程如下:45钢试片打磨抛光→丙酮洗涤→质量分数5%的氢氧化钠溶液浸泡→体积分数10%的盐酸溶液浸蚀→去离子水洗涤→冷风吹干→磷化→去离子水洗涤→冷风吹干。
为了获得足够的样本数据用于建立预测模型,在不同工艺参数下制备磷化膜。选取对磷化膜耐蚀性影响较大的3个因素——磷化液温度、磷化液游离酸度、磷化时间作为输入参数,在实验筛选的基础上,确定每个参数的水平,如表1所示。按照一定规律组合进行27组实验,图1为45钢试片及磷化膜的宏观形貌,可见成膜完整且均匀,磷化膜呈灰黑色。
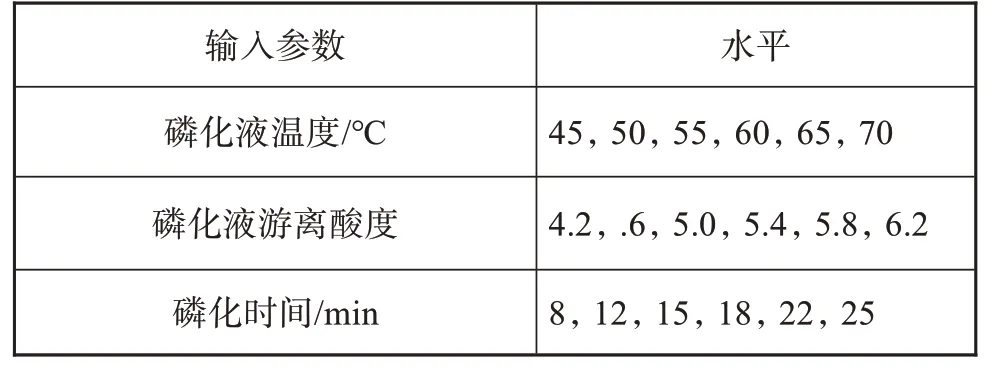
表1 输入参数及其水平Tab.1 Input parameters and its levels

图1 45钢片及磷化膜的宏观形貌Fig.1 Macro-morphology of 45 steel sheet andphosphating film
1.2 磷化膜耐点蚀时间测定
根据GB 6807-86附录D配制检测溶液,采用点滴法测定磷化膜耐点蚀时间。大量研究已经证实,耐点蚀时间可以用来评价磷化膜耐蚀性[10-12]。磷化膜表面的液滴由蓝色变成淡红色或淡黄色经历的时间定义为耐点蚀时间,越长表明磷化膜耐蚀性越好。
2 预测模型建立及优化
2.1 预测模型建立
GRNN通常为四层结构,由输入层、模式层、求和层和输出层构成。笔者根据GRNN基本原理并结合其常规结构,建立用于预测磷化膜耐蚀性能的模型,如图2所示。其中,输入层有三个节点,分别对应磷化液温度(用X1表示,单位为℃)、磷化液游离酸度(用X2表示,无计量单位)、磷化时间(用X3表示,单位为min),输出层只有一个节点,对应磷化膜耐点蚀时间(用Y1表示,单位为s)。
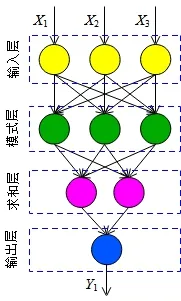
图2 用于预测磷化膜耐蚀性的模型结构示意图Fig.2 Structural schematic diagram of the model used to predict the corrosion resistance of phosphating film
需要说明的是,建立预测模型时需对模型平滑因子(σ)寻优,筛选出适宜的平滑因子是保证模型具有良好性能的关键。原因是平滑因子较小时,可能导致模型无法收敛。而平滑因子较大时,模型易出现过拟合现象,导致预测结果近似于样本数据的均值。
平滑因子寻优传统的方法是试凑法和经验法,这两种方法都存在寻优速度慢且结果不准确的问题。果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)具有较强的局部搜索能力,适用于非线性优化问题。粒子群优化(Particle Swarm Optimization,PSO)算法是近些年发展起来的一种智能随机优化算法[13-14],具有全局搜索寻优的特性,不容易陷入某个局部最优解而无法跳出,在保证收敛的同时寻优速度较快且结果准确度高,也适用于非线性优化问题。为此,分别采用FOA算法、PSO算法对平滑因子寻优进而优化预测模型,并比较不同算法的优化效果。
2.2 预测模型优化
FOA算法是一种基于果蝇觅食行为推演的一种全局寻优算法,采用FOA算法对平滑因子进行寻优进而优化预测模型的流程如图3所示,说明如下:(1)参数初始化,比如果蝇的种群规模、迭代次数和初始位置;(2)随机赋值果蝇个体初始位置、方向;(3)计算得到特征参数;(4)迭代寻优;(5)输出全局最优值,并代入GRNN模型完成优化。

图3 采用FOA算法对平滑因子寻优进而优化预测模型的流程Fig.3 Flow of optimization of smoothing factor using FOA algorithm and then optimize the prediction model
采用PSO算法对平滑因子寻优进而优化预测模型的流程如图4所示,说明如下:(1)对样本数据进行预处理,并分成指定数量的训练样本和检验样本;(2)将训练样本数据导入GRNN模型中,根据初始化粒子计算各粒子适应度;(3)求取模型的个体极值和种族极值;(4)以模型适应度为标准,更新粒子速度和位置;(5)检验模型是否满足精度要求或达到要求的迭代次数,达到条件后完成PSO-GRNN模型训练;(6)使用检验样本对建立好的PSO-GRNN模型进行检验,实现模型验证与性能评价。
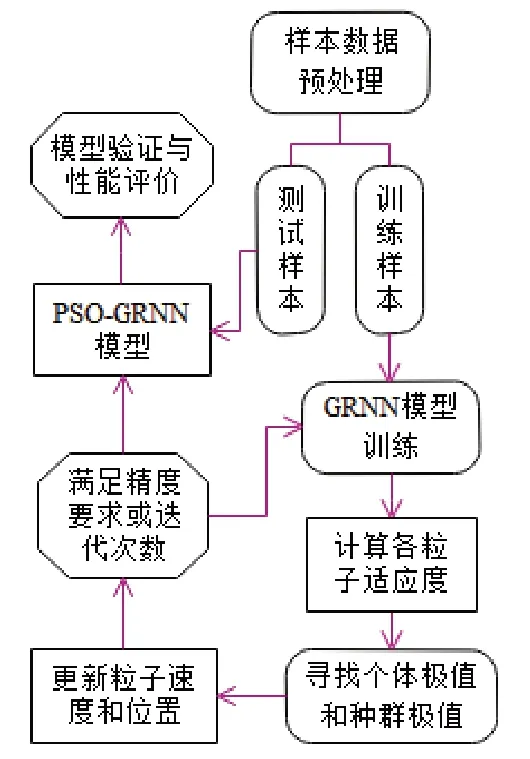
图4 采用PSO算法对平滑因子寻优进而优化预测模型的流程Fig.4 Flow of optimization of smoothing factor using PSO algorithm and then optimize the prediction model
3 预测模型训练
由于各组样本数据所处的量级存在差异,需进行归一化处理。处理后的27组样本数据中随机选取18组作为训练样本,用于优化后模型训练,剩余的9组作为检验样本,用于对优化后的预测模型的预测准确度进行检验评价。
在MATLAB中建立预测模型,调用函数net=newgrnn(P,T,spread)进行模型训练。其中,P表示输入量X=[X1,X2,X3],T表示输出量Y=Y1,spread表示平滑因子。考虑到训练样本数量相对较少,为提高预测模型训练的准确度,采用交叉验证方法进行训练。交叉验证的原理是将27组原始样本数据按一定比例划分成训练样本和检验样本,轮换训练样本、检验样本进行多次交叉验证,可根据较少的样本数据获取更多信息。本实验中进行3次交叉验证,即训练样本、检验样本轮换3次,如图5所示。3次交叉验证实现样本数据轮换交叉训练过程,增加了训练次数使模型得到充分训练。

图5 训练样本和检验样本交叉验证示意图Fig.5 Schematic diagram of cross-validation between training samples and test samples
平滑因子的求取分别采用常规循环法、FOA算法、PSO算法,通过对比最优目标函数适应度和求取最优目标函数适应度的用时,筛选出较佳的方法。
采用常规循环法求取最优平滑因子σbest的思路是:在给定的区间[0,2]内每隔0.01取一个平滑因子,根据目标函数适应度循环求取最优平滑因子。图6为采用常规循环法求取最优平滑因子的适应度曲线,可见经过3次交叉验证后,目标函数适应度趋近最小、为25.49,对应的最优平滑因子为0.24,求取最优平滑因子用时7.89 s。

图6 采用常规循环法求取最优平滑因子的适应度曲线Fig.6 Fitness curve of the optimal smoothing factor obtained with conventional cycle method
采用FOA算法求取最优平滑因子σbest的思路是:设置FOA算法迭代次数为100,种群数量为30。选取因变量相对误差作为目标函数适应度,通过迭代使因变量相对误差趋近最小,求取最优平滑因子。图7为采用FOA算法求取最优平滑因子的适应度曲线,可见经过21次迭代后均方差收敛至14.448并保持稳定直至迭代结束。
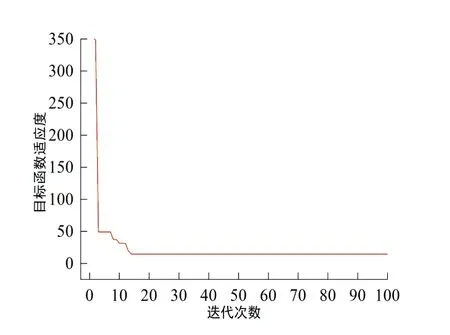
图7 采用FOA算法求取最优平滑因子的适应度曲线Fig.7 Fitness curve of the optimal smoothing factor obtained with FOA arithmetic
采用PSO算法求取最优平滑因子σbest的思路是:设置PSO迭代次数为100,种群数量为30,选取因变量相对误差作为目标函数适应度,通过迭代使因变量相对误差趋近最小,求取最优平滑因子。图8为采用PSO算法求取最优平滑因子的适应度曲线,可见经过23次迭代后目标函数适应度趋近最小、为12.27,求取最优平滑因子用时2.46 s。

图8 采用PSO算法求取最优平滑因子的适应度曲线Fig.8 Fitness curve of the optimal smoothing factor obtained with PSO arithmetic
将求取的最优平滑因子代入不同算法优化后的预测模型(即FOA-GRNN模型、PSO-GRNN模型)中,选取9组样本数据进行预测。图9为不同模型的预测值对比,可知常规BPNN模型和FOA-GRNN模型的预测值与真实值都存在一定差异,而PSOGRNN模型的预测值非常接近真实值,说明其预测准确度较高。
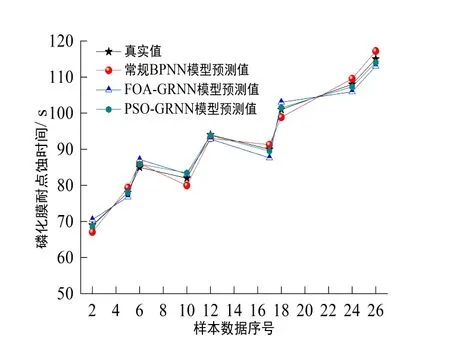
图9 不同模型的预测值对比Fig.9 Comparison of the predicted value of different models
为了进一步评价FOA-GRNN模型、PSO-GRNN模型的预测准确度,选取9组样本数据的预测相对误差和均方根误差作为指标,也与常规BPNN模型进行对比。图10为不同模型的预测相对误差,可知常规BPNN模型的预测相对误差在[0.963,2.834]区间内,最大相位误差为2.834%,最小相位误差为0.963%。FOA-GRNN模型的预测相对误差在[0.365,2.553]区间内,最大相对误差为2.553%,最小相对误差为0.365%。PSO-GRNN模型的预测相对误差在[0.001,1.778]区间内,最大相对误差为1.778%,最小相对误差趋近于0。相对误差越小说明预测值越趋近于真实值,即FOA-GRNN模型的预测准确度较高。

图10 不同模型的预测相对误差Fig.10 Prediction relative error of different models
PSO-GRNN模型的均方根误差为0.682,相比常规BPNN模型、FOA-GRNN模型的均方根误差分别减小了1.154、0.948。均方根误差较小同样说明PSO-GRNN模型的预测准确度较高,这也反映出PSO-GRNN模型具有突出的性能优势,对磷化膜耐蚀性的预测效果良好。
4 结论
引入广义回归神经网络建立了用于预测磷化膜耐蚀性的模型,并采用不同算法对平滑因子寻优进而优化预测模型。常规BPNN模型和FOA-GRNN模型的预测值与真实值都存在一定差异,预测相对误差范围较宽。PSO-GRNN模型的预测值非常接近真实值,最大相对误差为1.778,均方根误差最小、仅为0.682,其预测准确度较高,对磷化膜耐蚀性预测效果良好。

