考虑车钩垂向约束的机车轴重转移计算方法研究

张志超，李 谷，储高峰，祖宏林

(中国铁道科学研究院集团有限公司机车车辆研究所，北京 100081)

机车牵引列车起动或运行时，作用于机车的轮周牵引力和车钩力不在同一高度，会产生一个促使机车发生点头运动的力矩，从而引起机车各轴轴重的重新分配。轴重转移会影响机车黏着重量的利用和牵引力的发挥，减小机车轴重转移是提高黏着利用率的重要措施[1-4]。目前为止，针对该问题已经开展了广泛而深入的研究工作，得到了很多轴重转移计算方法和公式[5-19]。这些计算方法大致可分为两类：1)几何关系推导法[1,5-13]，根据车体、构架、轮对的相对位置关系以及一系、二系变化关系，并结合力的平衡关系解析推导机车实际轴重转移量；2)仿真计算分析法[14-18]，采用多体动力学分析软件建立机车动力学分析模型，利用该模型计算机车牵引时的轴重转移稳态值。几何关系推导法往往针对特定车型进行公式推导和求解，表达式相对复杂，通用性较差，难以模拟车钩高度、牵引点高度变化对轴重转移的影响。仿真计算分析法虽然通过仿真分析能够得到更为接近机车实际运行工况的轴重转移特性，但是同样存在通用性问题，不同类型机车需要重新建模，而且为了考虑电机对轴重转移的影响需要建立详细的电机系统模型。因此，为了实现高效快捷的机车轴重转移计算以及牵引黏着特性设计，有必要建立具有通用性的机车轴重转移计算方法。

另外，目前的机车轴重转移计算分析只考虑了车钩纵向牵引力的影响，并未考虑在纵向拉钩力作用下连挂车钩钩头接触面对机车后端垂向运动的约束作用。这种简化使得机车不受额外垂向作用力，因此车体基本没有垂向位移，只会产生绕其质心的点头转动，如图1(b)所示。此时虽然机车各轴间的轴重会发生转移，但是各轴轴重总和保持不变。然而，机车实际牵引列车时，其后端连挂车钩高达数百千牛的纵向拉钩力会使得钩头接触面产生垂向摩擦力，抑制车钩及机车后部产生垂向位移，当该垂向位移被完全约束时，机车将产生如图1(c)所示的以后端车钩连挂点为中心的点头转动。此时机车车体运动形态的变化势必带来各轴轴重转移的变化，并且各轴轴重总和也不再保持不变。连挂车钩垂向约束作用的影响在以往各种机车轴重转移计算方法中均未曾予以考虑，因此十分有必要明确它对轴重转移的具体影响程度和规律。

图1 机车牵引时车体运动形态示意图Fig. 1 Schematic diagram of locomotive carbody motion during traction

针对上述机车轴重转移计算存在的两个问题，本文将机车后端连挂车钩的垂向约束作用等效为线性弹簧约束，通过等效约束刚度的大小来模拟后端车钩垂向约束作用的强弱；并考虑牵引杆布置方式、牵引点高度变化的影响，通过机车受力平衡分析推导了机车轴重转移计算公式，建立了具有通用格式的轴重转移计算矩阵方程，为机车轴重转移计算提供了具有统一性的新方法。在此基础上，针对2(B0-B0)轴式机车分析了连挂车钩垂向约束的影响规律，针对C0-C0 轴式六轴机车详细分析了一系和二系弹簧刚度、牵引点高度等因素对轴重转移的影响规律。

1 考虑车钩垂向约束的机车轴重转移计算方程

正如前文所述，连挂车钩钩头垂向摩擦作用会对机车的轴重转移产生影响，因此需要在分析模型中予以考虑。一般而言车钩钩头的摩擦约束作用呈现非线性特性，并且车钩本身相对车体还具有一定范围的垂向自由转动，难以在轴重转移静态计算中实现。为此，本文将其简化等效为具有一定刚度的线性弹簧约束，通过改变等效约束刚度的大小来体现车钩钩头垂向约束作用的强弱，如图2 所示。

图2 机车轴重转移分析图Fig. 2 Diagram of locomotive axle load transfer

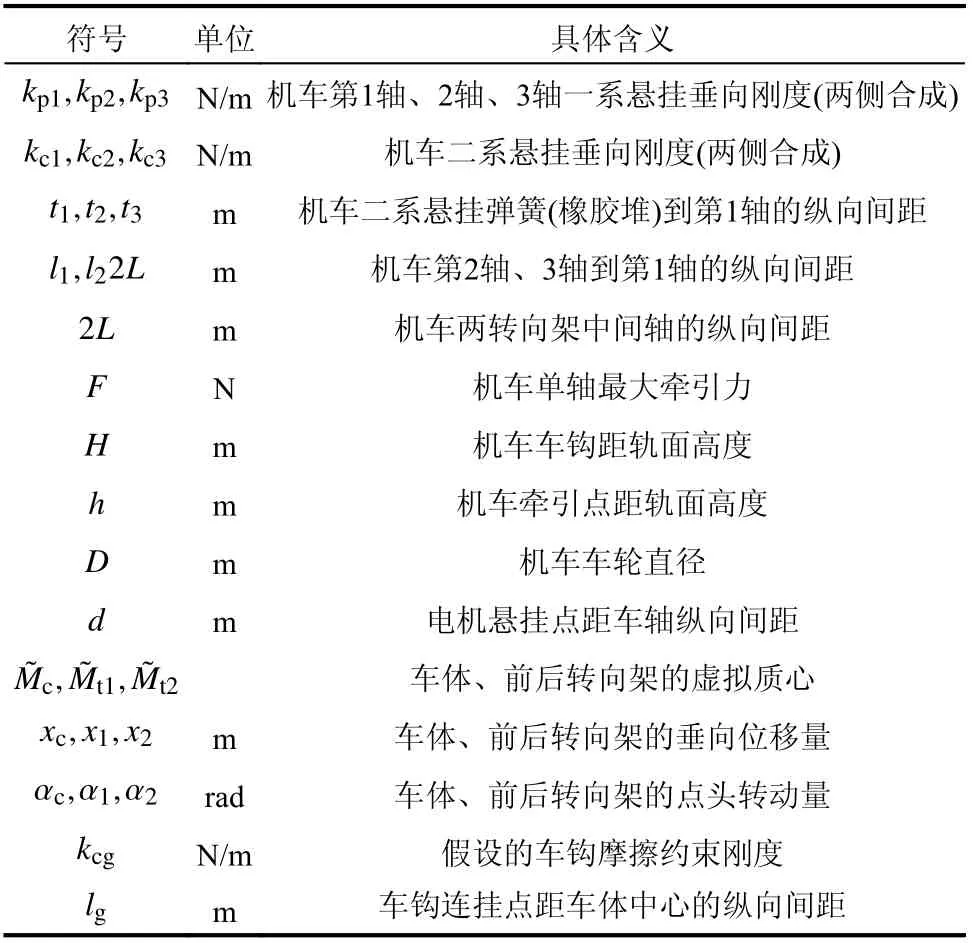
表1 各符号物理含义说明Table 1 Description of physical meanings of symbols

根据车体、前后转向架的垂向力和力矩平衡关系，分别建立相应的平衡方程。车体垂向受力平衡方程：

前转向架垂向力平衡方程：

图3 牵引电机布置位置示意图Fig. 3 Diagram of traction motor arrangements

将式(1)～式(6)统一写成矩阵形式，可得：

通过式(7)～式(9)可以发现，方程式中K即为机车垂向振动方程的刚度矩阵[20]，矩阵中的每一项kij表示由于第j个单位位移而引起的第i个作用力；A为考虑车钩和牵引点高度变化时的系数矩阵，如果不考虑牵引点高度变化的影响可令Aij=0；X为车体和前后转向架位移向量；F为外力向量，提供车钩力和牵引电机作用力的作用信息，向量中各项可由受力分析方便得到。正因如此，可直接通过机车垂向振动模型受力分析来构建系统刚度矩阵和外力向量，这种方法比前述的几何关系推导法简单明了，且不易出错，其通用性主要体现在以下几个方面：

1)适用于C0-C0 轴式、2(B0-B0)轴式等多种结构形式机车。虽然以上轴重转移求解矩阵是针对六轴机车推导建立的方程，对于单节四轴机车同样适用，只需要在转向架两轴中间加一条虚拟轴，在二系悬挂中间加一对虚拟弹簧(橡胶堆)，并将虚拟轴和虚拟弹簧(橡胶堆)的刚度设为0。

2)适用于不同牵引杆类型的情况。能够方便处理牵引杆为斜拉杆的机车，当二轴转向架机车采用斜牵引杆时，只需在式(7)的右侧附加另一外力向量：

其中， θ为牵引拉杆与水平面的夹角。这里规定，当牵引杆位于车体中部时 θ为正值，位于车体两端时 θ为负值。

3)上述方程推导针对牵引电机轴悬式机车，对于牵引电机架悬式机车，只需要修改方程式(7)中的电机相关系数即可。

通过求解方程式(7)可以得到机车牵引列车时的各部分垂向位移和点头角位移，进而方便地得到各轴轴重变化量：

由式(11)计算得到各轴轴重转移量后便可求解各轴的黏着系数利用率，进而可以方便快捷地分析机车的理想牵引高度等。

2 后端连挂车钩垂向约束影响分析

本文计算模型中采用具有一定刚度的线性弹簧约束来等效模拟后端连挂车钩的垂向约束作用，通过改变等效约束刚度的大小来体现车钩钩头垂向约束作用的大小。假设该等效约束刚度从0 kN/m 到1×1015kN/m 逐渐增大，分别计算不同等效约束刚度下的机车轴重转移情况。

采用某HX 系列重载电力机车计算参数，轴式为2(B0-B0)，牵引电机装置采用轴悬式对称布置。表2 列出了不同等效约束刚度下的机车轴重变化和前钩钩头垂向位移。图4～图6 分别给出机车运动形态、机车各轴黏着利用率以及前端车钩抬升量随等效约束刚度的变化曲线图。

表2 不同车钩等效约束刚度下机车轴重转移情况Table 2 Locomotive axle load transfer under different coupler equivalent restraint stiffness

图4 各部分运动变化量随等效约束刚度变化曲线图Fig. 4 Variation of locomotive carbody motions with coupler equivalent restraint stiffness

表2 中后端车钩等效约束刚度为0 即为不考虑后端车钩垂向摩擦约束作用的情况。由表2、图4 可见，随着等效约束刚度的增大，机车车体和转向架运动形态会发生变化，车体垂向位移和点头角位移逐渐减小，前、后转向架垂向位移在原有基础上逐渐增大，而它们的点头角位移基本保持不变，这说明随着后端车钩钩头约束作用的增大，前、后转向架运动的增大一定程度上弥补了车体运动的减小。

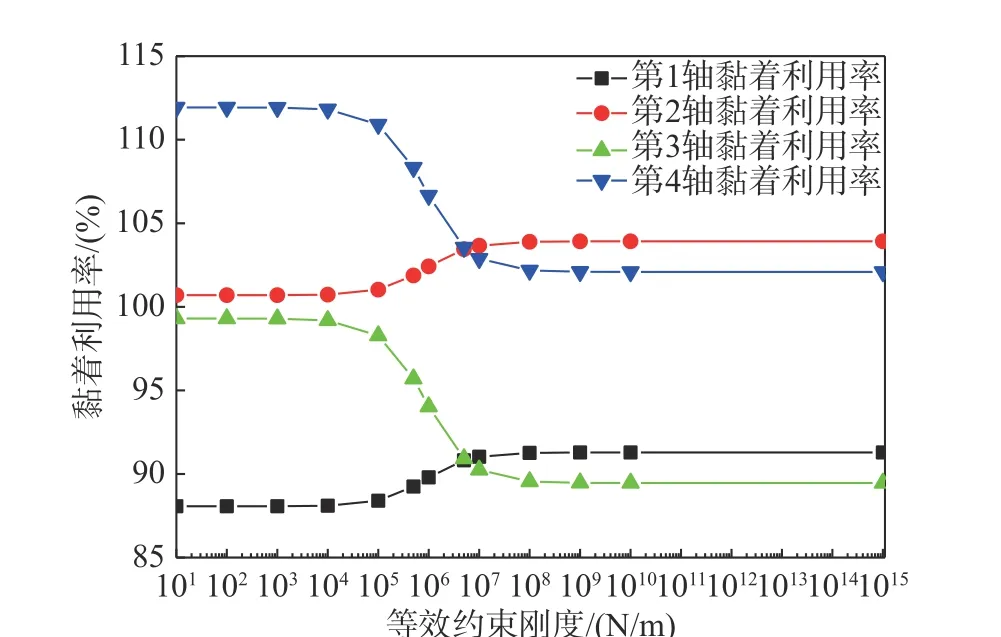
图5 机车各轴黏着利用率随等效约束刚度变化曲线图Fig. 5 Variation of locomotive adhesion utilization ratios with coupler equivalent restraint stiffness

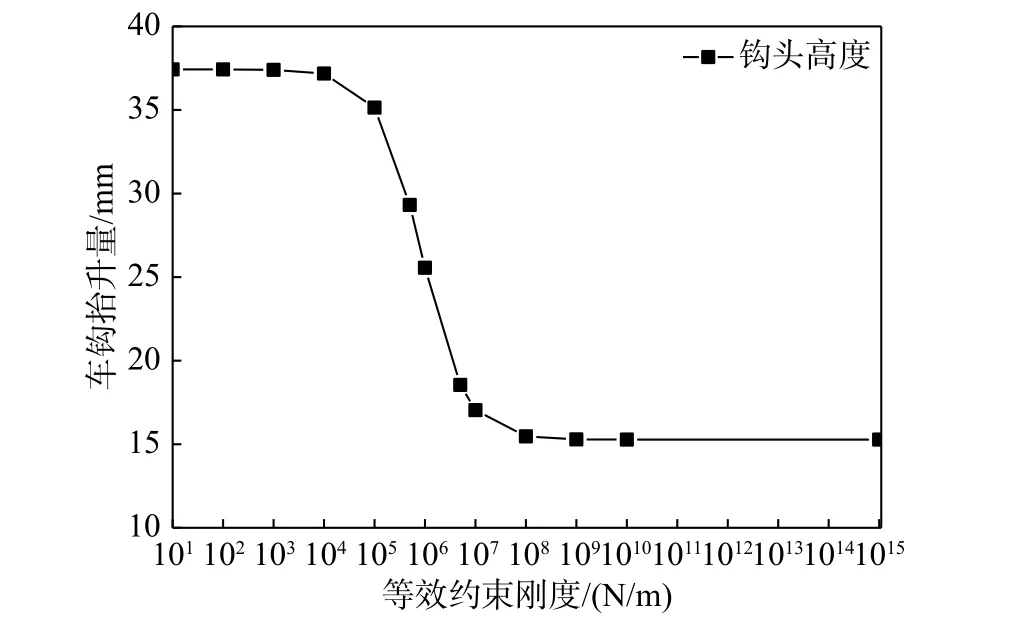
图6 机车车钩抬升量随等效约束刚度变化曲线图Fig. 6 Variation of coupler lifting with coupler equivalent restraint stiffness

当不考虑后端车钩垂向约束(等效约束刚度为0)时，第1 轴、3 轴轴重处于减载状态，第1 轴减载量达到29.236 kN；随着等效约束刚度的增大，机车各轴轴重有明显变化，第1 轴、3 轴虽然仍处于减载状态，但是随着后端车钩垂向约束的增大，第1 轴减载逐渐减弱，而第3 轴减载量逐渐增大并超过第1 轴。相应地，机车各轴黏着利用率具有与轴重相同的变化规律，而根据机车黏着利用率等于各轴最小黏着利用率的原则，从图4可以看出，在等效约束刚度小于5×106N/m 时，机车黏着利用率取第1 轴黏着利用率，且逐渐减小；而在等效约束刚度大于5×106N/m 后，便取第3 轴黏着利用率，且逐渐增大。另外，机车各轴总轴重随着后端车钩垂向约束的增大会出现逐渐增大的减载量，当等效约束刚度1×1015N/m 时，即后端车钩完全约束状态时，整个机车约减载3.2%。

最后分析前端车钩抬升量随后端车钩垂向约束作用的变化规律。用于计算分析的重载机车专门进行了机车满功率牵引起动时的车钩抬升量测定试验，具体方法为：重载列车停放于平直道，后部货车大列施加空气制动，前部机车施加牵引力，在前端钩头下部设置一块调整为水平状态的平板，在钩头位置布置垂向激光测距仪对准平板测量车钩抬升量。当机车施加满级牵引力760 kN时，前端车钩抬升量测定值为20 mm，介于等效约束刚度为0 N/m 和1×1015N/m 之间，说明机车实际牵引时，后端车钩确实在拉钩力作用下对车体产生了垂向约束作用，但是该垂向约束并未达到完全刚性约束状态，充分印证了本文的分析结论。从表2 中可知，当等效约束刚度取5×106N/m时，车钩抬升量18.55 mm，接近实际测定值，因此在实际轴重转移计算时，可以将等效约束刚度取值控制在5×106N/m 左右。此时根据表2 计算可得，该机车黏着利用率由不考虑车钩垂向约束作用的88%提高至等效约束刚度取值5×106N/m 时的91%，提高了3%。

3 六轴机车轴重转移影响因素分析

本节采用所建立的通用计算方法对某C0-C0轴式电力机车的轴重转移情况进行计算，分析机车一系和二系悬挂垂向刚度、牵引点高度等因素对其轴重转移的影响。机车轴重25 t，每轴起动牵引力为95 kN，车钩距离轨面高度0.88 m，转向架第1 轴、3 轴距离第2 轴的纵向距离分别为2.25 m、2.00 m，定距为12.32 m，牵引方式采用水平牵引杆，电机吊挂方式为轴悬式，电机吊杆到车轴的纵向距离为1.171 m，每轴一系悬挂垂向合成刚度为3400 kN/m，二系悬挂采用橡胶堆，每个纵断面橡胶堆垂向合成刚度为12 000 kN/m，二系橡胶堆到转向架第1 轴的纵向距离分别为1.1825 m、1.5175 m、3.35 m。

首先分析机车一系垂向刚度对轴重转移的影响，假设一系垂向刚度在2200 kN/m～4600 kN/m每隔400 kN/m 取值，图7 给出了机车各轴轴重变化量随一系垂向刚度的变化曲线图，图8 给出了相应的黏着系数利用率随一系垂向刚度的变化规律图。可以看出，随着一系垂向刚度的增大，机车第1 轴减载量逐渐增大，第2 轴减载量逐渐减小，第3 轴由减载逐渐变为增载，机车黏着系数利用率逐渐减小。

图7 各轴轴重变化量随一系垂向刚度变化曲线图Fig. 7 Variation of locomotive axle load transfer with primary suspension vertical stiffness

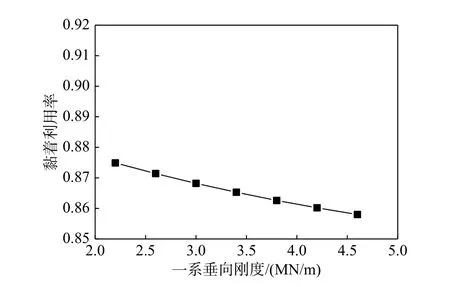
图8 机车黏着系数利用率随一系垂向刚度变化规律图Fig. 8 Variation of locomotive adhesion utilization ratios with primary suspension vertical stiffness

假设二系垂向刚度在9000 kN/m～15 000 kN/m范围内每隔1000 kN/m 取值，分析二系垂向刚度变化对机车轴重转移的影响。图9 给出了机车各轴轴重变化量随二系垂向刚度的变化曲线图，图10给出了相应的黏着系数利用率随二系垂向刚度的变化规律图。可以看出，随着二系垂向刚度的增大，机车第1 轴减载量逐渐减小，第2 轴减载量逐渐增大，第3 轴增载量逐渐减小，后转向架三个轴与前转向架正好相反，且机车黏着系数利用率逐渐增大。二系垂向刚度增大会使得二系垂向位移减小，转向架转角相应减小，从而减弱机车轴重转移。假设机车牵引点高度从-75 mm～725 mm 按照间隔100 mm 递增，分析牵引点高度变化对机车轴重转移的影响。图11 给出了机车各轴轴重变化量随牵引点高度的变化曲线图，图12 给出了相应的黏着系数利用率变化规律图。可以看出，当牵引点高度为负值或者很小时，第3 轴轴重减载大于第1 轴，且减载量随牵引点高度增大逐渐减小；随后当前牵引点高度逐渐增大时，第1 轴轴重减载逐渐增大，第2 轴轴重减载量逐渐减小，机车黏着系数利用率随之明显减小。可见牵引点高度对轴重转移具有明显影响，其影响程度要大于一系和二系悬挂垂向刚度。

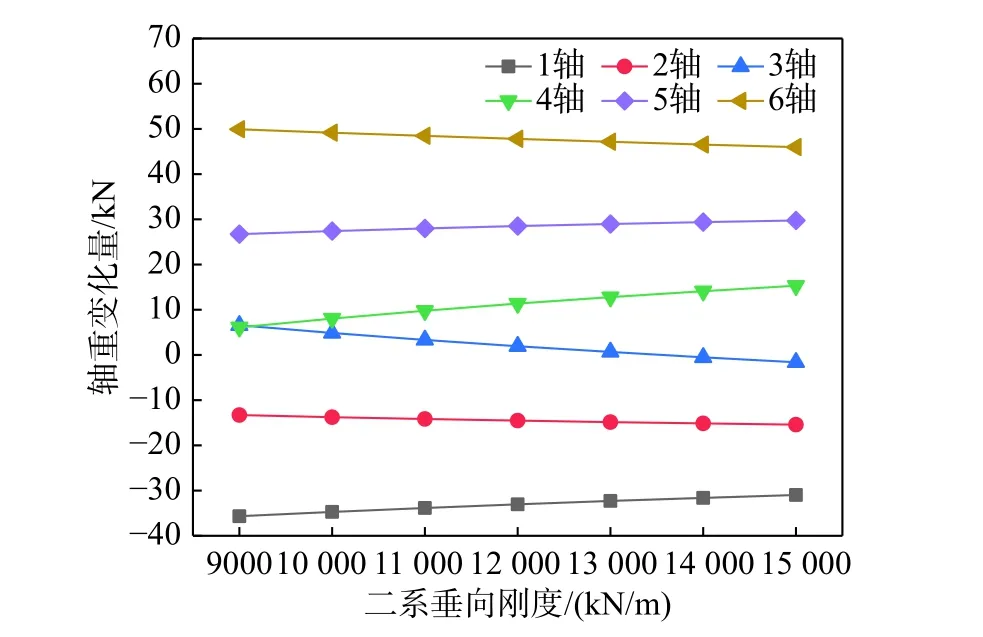
图9 各轴轴重变化量随二系垂向刚度变化曲线图Fig. 9 Variation of locomotive axle load transfer with secondary suspension vertical stiffness

图10 机车黏着系数利用率随二系垂向刚度变化规律图Fig. 10 Variation of locomotive adhesion utilization ratios with secondary suspension vertical stiffness

图11 各轴轴重变化量随牵引点高度变化曲线图Fig. 11 Variation of locomotive axle load transfer with traction point height

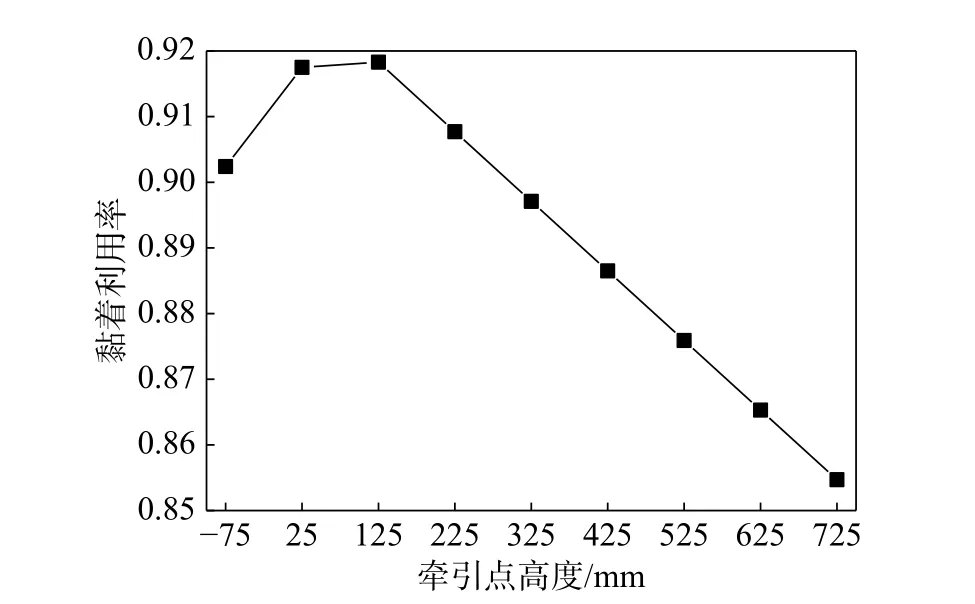
图12 机车黏着系数利用率随牵引点高度变化规律图Fig. 12 Variation of locomotive adhesion utilization ratios with traction point height

4 结论及展望

针对机车轴重转移计算相关问题，本文建立了考虑车钩垂向约束作用的机车轴重转移通用计算方法，结合试验数据确定了车钩等效约束刚度的取值范围，并采用所编制的计算程序分析了后端车钩垂向约束、结构悬挂参数等对机车轴重转移的影响规律。研究结论主要包括以下几点：

(1)机车牵引时后端连挂车钩钩头接触面在拉钩力作用下产生的垂向约束作用会对机车轴重转移产生明显影响，结合某HX 系列2(B0-B0)轴式机车车钩抬升量试验结果确定该车等效约束刚度合理的取值约为二系橡胶堆到转向架第1 轴的纵向距离为5×106N/m，其黏着利用率较不考虑车钩垂向约束时提高了3%。

(2)所建立的基于刚度矩阵的机车轴重转移计算方法能够综合考虑牵引点高度变化、机车斜拉杆的影响作用，简便、准确地对各种类型机车进行轴重转移计算，具有较好的通用性。

(3)机车悬挂参数和牵引点高度均对其轴重转移具有影响作用，并且牵引点高度影响最为显著，牵引点高度增大会加剧轴重转移。

目前机车轴重转移主要通过计算分析得到，轴重转移相关试验研究很少见到。正因如此，机车轴重转移的计算分析结果并未通过试验数据进行验证和修正，本文并未得到各轴轴重变化量测试数据，仅通过机车牵引工况的前端车钩抬升量测定试验对计算结果进行了侧面校验。为了校验和改进机车轴重转移计算方法，有必要开展机车轴重转移试验测试相关研究工作。