模块化多电平换流器电容用量的标幺化分析与设计方法

周月宾，宋强，杨柳，张楠，李政轩，曹琬钰

(1. 直流输电技术国家重点实验室(南方电网科学研究院)，广州市 510663；2. 电力系统及大型发电设备安全控制和仿真国家重点实验室(清华大学)，北京市 100084；3.中国南方电网有限责任公司超高压输电公司检修试验中心，广州市 510663)

0 引 言

模块化多电平换流器(modular multilevel converter, MMC)已经成为高压柔性直流输电换流器的主要方案[1-2]。MMC具有易实现大电平数目、谐波性能好、损耗低、可模块化设计等优势。但是MMC 各桥臂的功率波动无法在三相间相互抵消，为了限制子模块电容电压波动的幅度，MMC 所需要的子模块电容巨大。目前，直流电容在子模块体积中一般占到60%～80%，造价甚至与所需开关器件接近[3-5]。MMC的整体电容用量是影响装置体积和成本的关键因素，如何对MMC的电容用量进行衡量、分析和设计就成为非常关键的问题[6-12]。

在目前的MMC分析与设计方法中，通常是将子模块电容值作为直接设计指标。一般的方式是对子模块电容电压波动进行解析分析，得到描述电容电压波动率限值和子模块电容值关系的计算公式，计算公式还包含MMC输出电流、功率因数角、子模块额定电压、桥臂级联子模块数目等参数。在相关参数已知的情况下，计算出所需的子模块电容值[13-17]。或者通过数字仿真等手段进行扫描计算得到所需的子模块电容值。

当直接以子模块电容值作为设计指标时，对于一个额定容量确定的MMC，当交、直流侧额定电压、桥臂级联子模块数目、子模块额定电压等相关参数发生变化时，所需的子模块电容值都会发生变化，无法单独利用电容值明确表征MMC电容用量。由于MMC的多种参数变化都会影响电容值计算结果，也难以清晰确定对MMC整体电容用量影响的关键因素，无法对参数优化的设计提供明确指导。另一方面，子模块电容的体积和成本与电容值和额定电压都相关，并且MMC整体电容总用量还受到子模块总数量影响。因此，难以利用子模块电容值直接分析MMC电容用量对装置成本和体积影响，也无法作为不同额定参数MMC之间电容用量分析和比较基准。

电容中储存的能量是由电容值与电容电压平方的乘积决定的，实际上这也反映了电容的体积和成本与电容值和电容额定电压之间的关系。因此，有文献提出将所有子模块电容在额定电压时所储存的总能量作为衡量MMC电容用量的指标[18-20]。如果以MMC额定容量为基准进行归一化，进一步得到单位容量的MMC额定储能值，并以kJ/(MV·A)作为单位，则可以对不同参数的MMC的电容用量进行统一的衡量、分析和设计。在文献[21]中也定义了等容量放电时间常数，即将MMC 子模块电容所储存的总能量以等于MMC 额定容量的功率放电时所能持续的时间长度，这与单位容量MMC额定储能值所定义的指标是相同的，只是采用的单位不同。但是，现有研究仍仅是定义单位容量额定储能，并将其作为一种电容用量的衡量和比较指标，而不是作为参数设计过程中的直接计算目标。在设计过程中仍是先利用电容值计算公式计算出子模块电容值，再根据电容值间接计算出单位容量额定储能值。因此参数设计过程并没有本质改变，计算过程仍较为复杂，仍然需要利用到较多MMC具体参数，且不同参数MMC的额定储能值计算过程也难以统一。由于多种具体参数仍参与到计算过程中，对影响MMC额定储能值设计的关键因素及其影响规律的分析也难以得到统一和简化。

本文以单位容量额定储能值作为MMC电容用量的统一衡量与直接设计指标，建立直接描述MMC所需额定储能值与电容电压波动率之间关系的标幺化计算模型，可以在设计过程中直接计算出所需的单位容量额定储能值。储能值标幺化计算模型使不同额定参数MMC的电容用量的衡量、计算和分析可以得到统一和简化。基于所提出的储能值标幺化计算模型，揭示基准调制比和功率输出范围对MMC额定储能设计值影响的规律，为MMC电容用量的设计和优化提供明确的依据。数字仿真和物理试验结果验证所提出方法的正确性。

1 MMC额定储能值标幺化计算模型

1.1 桥臂功率波动分析

图1所示为基于半桥子模块的MMC的单相桥臂结构示意图。以A相为例，图中Uap和Uan分别表示上、下桥臂电压，iap和ian分别为上、下桥臂电流，us_a为电网电压，Udc为直流端口电压。图1中所示为半桥子模块，其中Cd为子模块电容值，Uc为电容电压。在MMC运行时，桥臂上的电压和电流的乘积产生桥臂功率波动，桥臂功率波动则引起子模块电容中所存储的能量的变化，使桥臂储能值发生波动，并体现在电容电压波动上。为了分析子模块电容电压波动的大小，可以从桥臂功率波动开始分析。

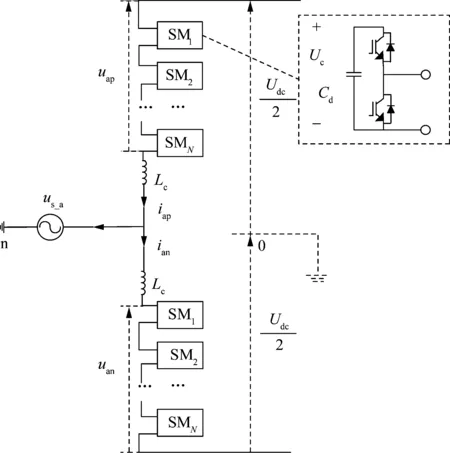
图1 MMC桥臂示意图Fig.1 Diagram of the arm of MMC

在忽略损耗的情况下，MMC与交流电网连接的等效电路如图2所示，图中交流电网电压相量为Us=Us∠0，其中Us为交流相电压额定有效值，Uac=Uac∠δ为MMC输出电压相量，Iac=Iac∠(-φ)为MMC输出电流相量，φ为功率因数角。图中X为MMC与交流电网之间的等效连接电抗，包括交流并网点与MMC之间的线路电抗、变压器漏抗和桥臂电抗等。当MMC输出给定的电流时，所需交流输出电压可表示为：

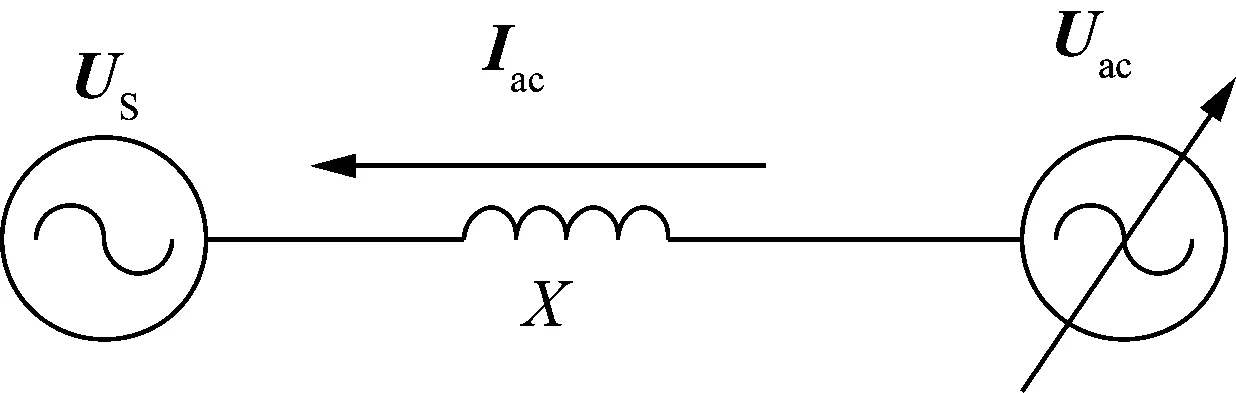
图2 MMC并网等效电路Fig.2 Equivalent circuit for an MMC connected to AC grid

Uac=Us+jXIac

(1)

MMC输出电压的有效值和相位角可表示如下：

(2)

(3)

以A相上桥臂为例进行分析， A相上桥臂电压可以表示如下：

(4)

A相上桥臂电流可以表示为[15]：

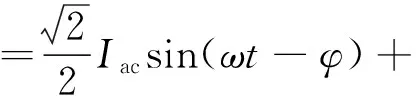
(5)

式中：Iac是MMC交流输出基波电流有效值；Idc是MMC直流侧电流；Iz是桥臂中二倍频环流有效值；β是二倍频环流相位角。

在式(4)和式(5)的桥臂电压、电流解析表达式中，既包括交流侧的电压和电流量，也包括直流侧的电压和电流量。为了分析方便，可以统一用交流侧的电压和电流量表示。MMC交、直流端口电压的关系可以用调制比来描述，即交流相电压峰值与直流端口电压的比值：

(6)

忽略MMC损耗，MMC交、直流端口功率应满足如下关系：

3UacIaccos(φ+δ)=UdcIdc

(7)

将式(7)代入式(6)中，可以得到MMC交、直流端口电流的关系如下：

(8)

将式(6)所表述的交直流端口电压关系代入到式(4)的桥臂电压表达式中，将式(8)所表述的交直流端口电流关系代入到式(5)的桥臂电流表达式中，使桥臂电压和电流的表达式中只包含交流侧的电压和电流量，然后代入式(9)计算桥臂功率波动：

parm(t)=uap(t)iap(t)

(9)

可得到桥臂功率波动基频分量、二倍频分量和三倍频分量的解析表达式分别如下：

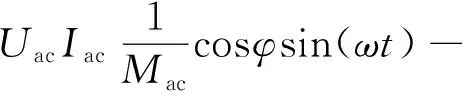
(10)

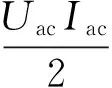
(11)

(12)

在正常参数设计情况下，二倍频环流比例Iz/Iac通常较小，对桥臂功率波动和电容电压波动的影响相对较小。另一方面，目前二倍频环流的控制方法也已比较成熟，可以实现将二倍频环流控制为0或其他目标值，不同控制目标下二倍频环流幅值和相位也不相同，对桥臂功率波动和电容电压波动的影响也比较复杂。由于二倍频环流对MMC其他性能也存在影响，所注入的二倍频环流也是受限的，对于电容用量的影响也有限。因此，出于简化分析的目的，本文暂只以环流被控制为0的情况进行分析，主要关注由桥臂电压和电流的直流分量和基频交流分量引起的功率波动。环流为0时的MMC电容用量分析结果可以作为一个基准，实际应用中根据二倍频环流控制目标，MMC电容用量将在此基准附近上下变化。在二倍频环流为零的情况下，功率波动的解析表达式如下：

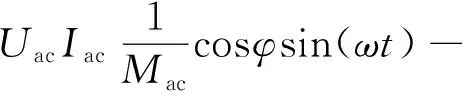
(13)

1.2 MMC电容储能值与电容电压波动的关系分析

子模块电容中储存有能量，假设桥臂中所有子模块电容电压相同，每个桥臂中储存能量的瞬时值可以表示为：

(14)

式中：N为桥臂级联子模块数目；ucap(t)为子模块电容电压瞬时值。桥臂功率波动对时间的积分引起桥臂储存能量的变化，桥臂储存能量瞬时值可表示为：

(15)

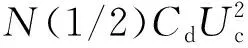
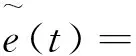
(16)

为了能够对不同参数的MMC进行统一分析，对计算模型采用标幺化处理，其中电压基值采用交流电网额定相电压Us，功率基值采用额定容量SN。假设MMC运行时电网电压保持为额定，交流电网侧视在功率标幺值如下：

(17)

根据式(2)和(6)，调制比随视在功率和功率因数角变化的解析表达式如下：

(18)

式中：X*为等效电抗标幺值；M0为基准调制比，也就是MMC在零功率输出时的调制比，即电网额定相电压峰值与直流母线电压的比值：

(19)

MMC交流输出电压和电网电压的关系也可以如下描述：

(20)

对桥臂储存能量值也以额定容量SN为基准进行归一化处理。根据式(17)，MMC单位容量储能值的波动分量如下：

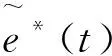
(21)

在一个基频周期内，桥臂储存能量波动的幅值可以表示为：

(22)

式中：T1为基频周期。以额定容量SN为基准，定义归一化的桥臂储存能量波动幅值为：

(23)

设子模块电容电压波动峰值相对于电容额定电压的差值为ΔUc，则桥臂储存能量波动幅值ΔE和电容电压波动幅值ΔUc的关系可以表示为：

ΔE=ΔE*SN=

(24)

定义子模块电容电压波动率为：

(25)

根据式(24)可以得到电容电压波动率的计算表达式：

(26)

当子模块电容电压为额定值Uc时，MMC的6个桥臂所有子模块中所存储的能量定义为MMC额定储能值：

(27)

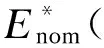
(28)

将式(28)代入到式(26)，可以得到电容电压波动率的标幺化计算方法如下：

(29)

从另一个角度来看，如果确定需要将电容电压波动率限制在ε以下，根据式(29)也可以得到对应此运行工况所需的MMC额定储能值计算方式如下：

(30)

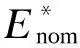
根据式(30)，显然电容电压波动率限值ε越大，所需的额定储能需求值就越小。当前工程设计中通常选择ε=10%对子模块电容进行设计。如果选择ε=20%，根据式(30)计算的额定储能需求值可以降为ε=10%时的47%。但是波动率限值ε的提高也会使电容电压波动峰值提高，造成器件电压应力加大。因此也有研究在提高波动率限值ε的同时相应降低电容额定电压值[22]。但是这又会带来桥臂子模块数量的少量增加，对整体电容用量的影响比较复杂。在本文的研究中仍以常用的ε=10%为例进行分析。

1.3 MMC额定储能设计值的计算

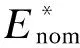
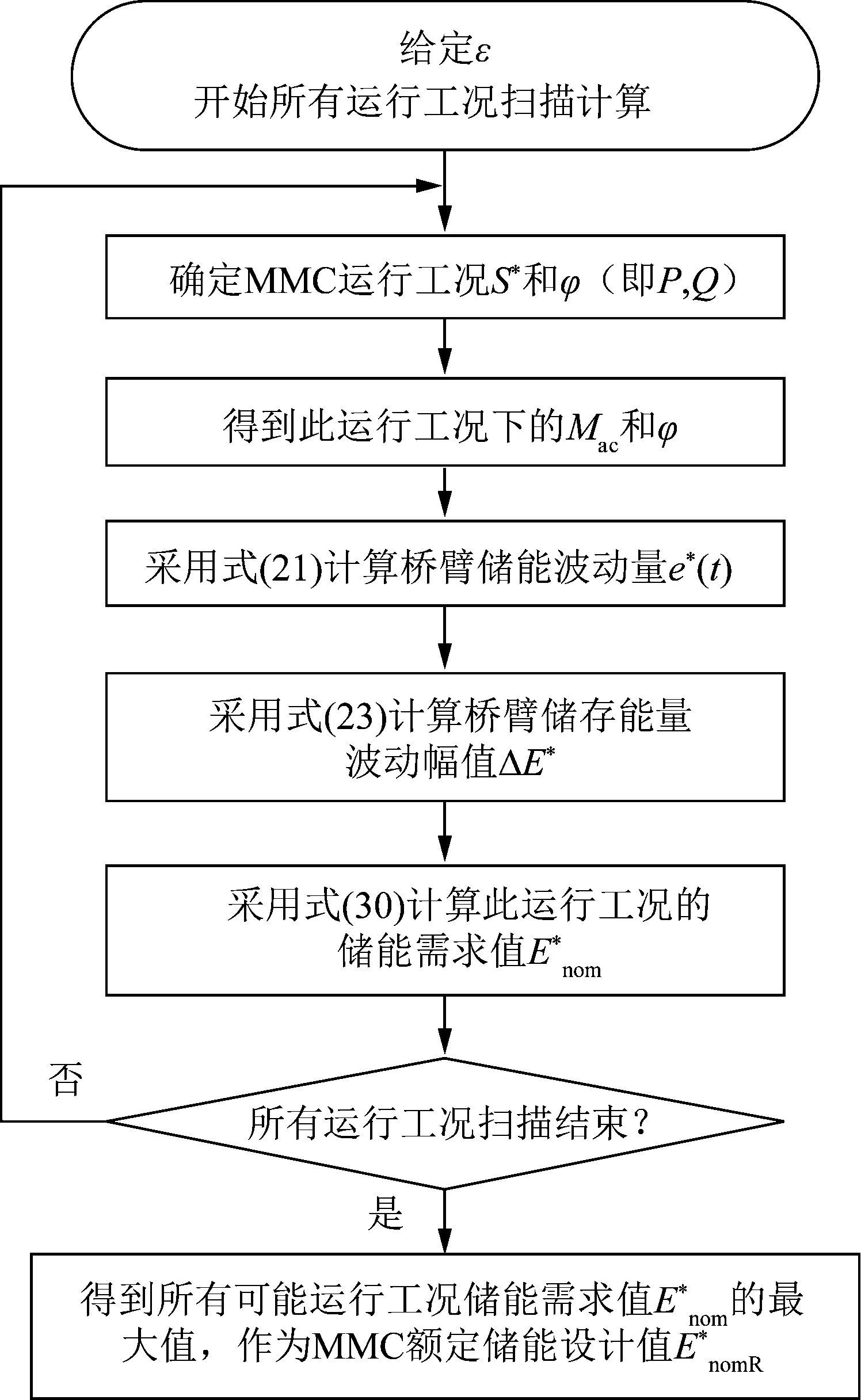
图3 MMC额定储能设计值计算流程Fig.3 Flowchart for calculating the rated energy storage of MMC

2 MMC额定储能设计值的影响因素分析

2.1 额定功率圆模式额定储能设计值分析

柔性直流输电换流器具有四象限输出能力，在能够输出足够高的电压的前提下，MMC的功率输出范围可以为如图4所示的PQ功率圆。对于常规的半桥子模块MMC，并且不考虑三次谐波注入方法时，调制比Mac能够达到的最大数值为1.0。如果MMC输出范围需要达到如图4所示的整个功率圆，根据式(19)，在设计交、直流电压额定值时应该使基准调制比M0满足如下条件：

(31)

考虑到电网电压波动等因素，M0的选择通常还应需留有一定的裕量。

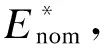
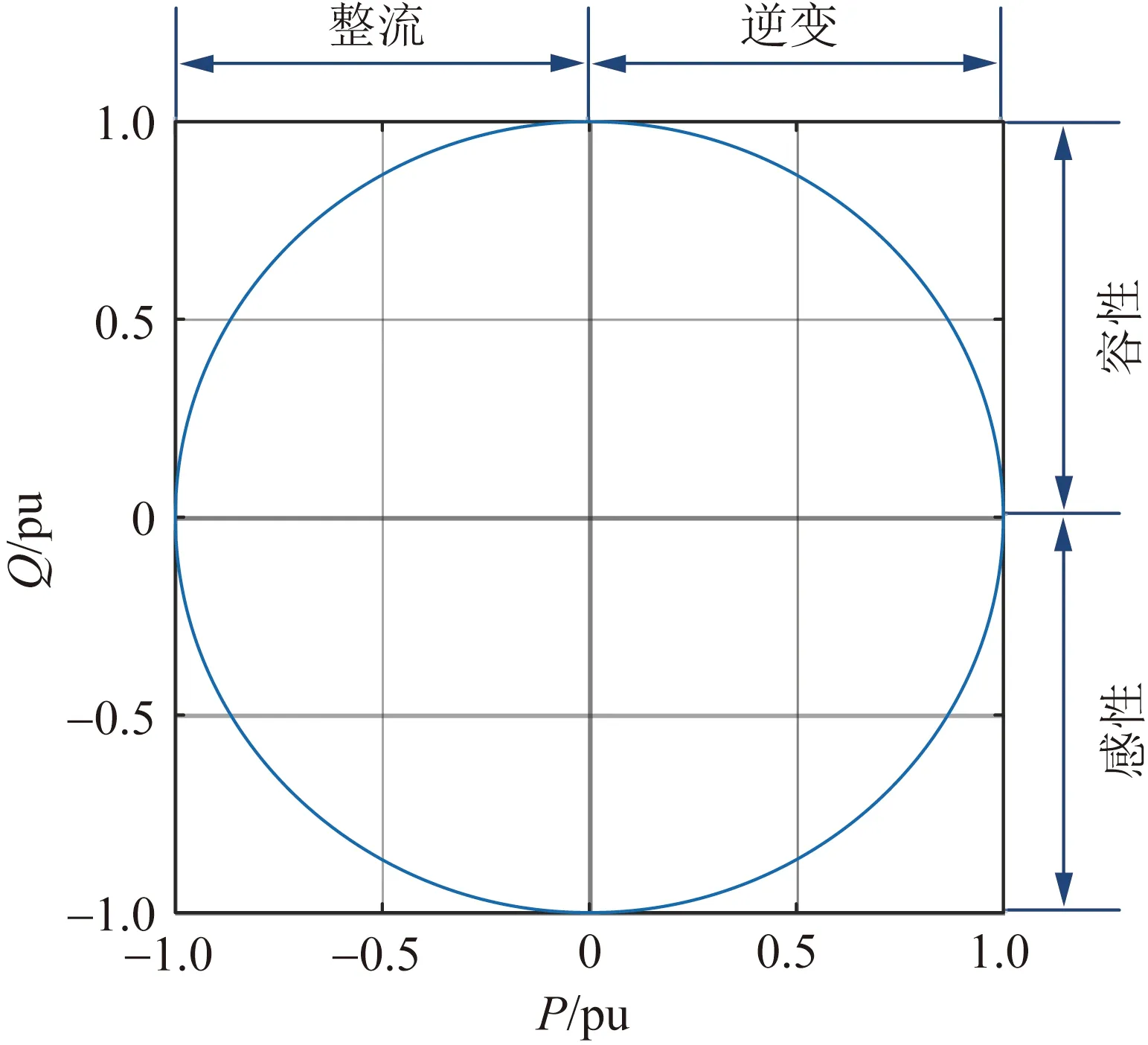
图4 MMC的PQ功率圆图Fig.4 PQ diagram of an MMC

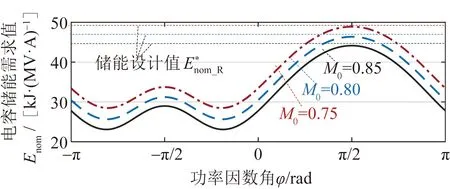
图5 MMC储能需求值随运行工况变化的曲线Fig.5 Curve of the values of energy storage requirement of MMC varying with power factor angle

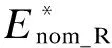
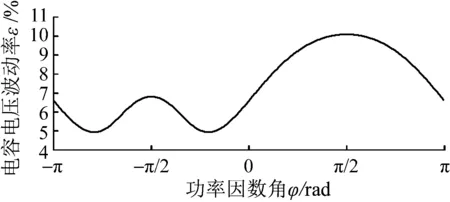
图6 运行点沿功率圆变化时的电压波动率曲线Fig.6 Curve of the capacitor voltage fluctuation rate varying with the power output.

2.2 最大容性无功限定模式电容用量分析

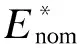
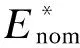
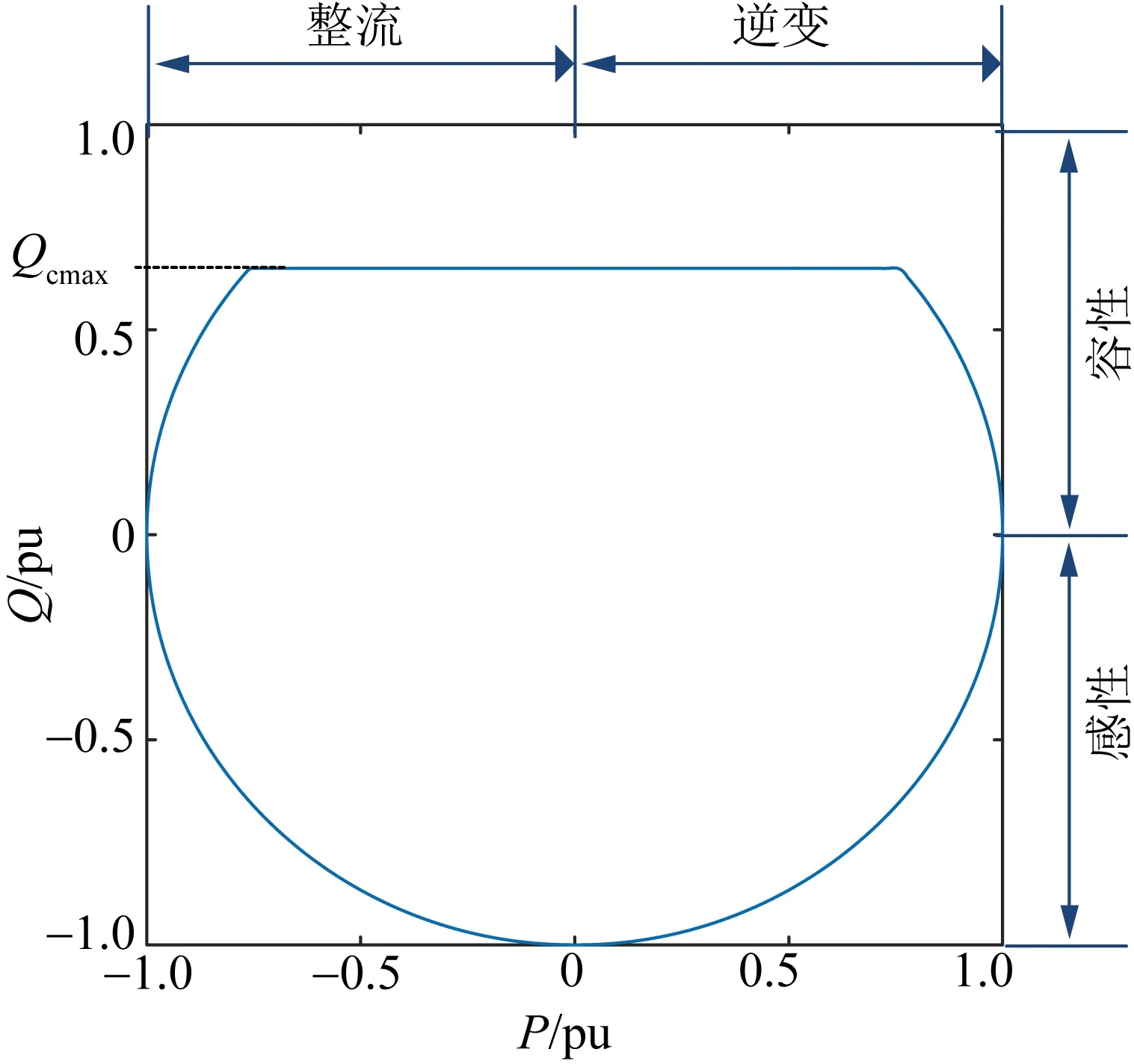
图7 最大容性无功限定模式的PQ功率圆图Fig.7 PQ diagram of MMC when limiting the maximum reactive power

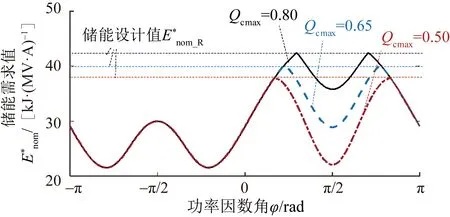
图8 最大容性无功限定模式下的MMC储能需求值随运行工况变化的曲线Fig.8 Curve of the values of energy storage requirement of MMC varying with power factor angle when limiting the maximum reactive pwoer

2.3 MMC基准调制比和功率输出范围对MMC储能设计值的影响分析

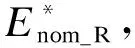
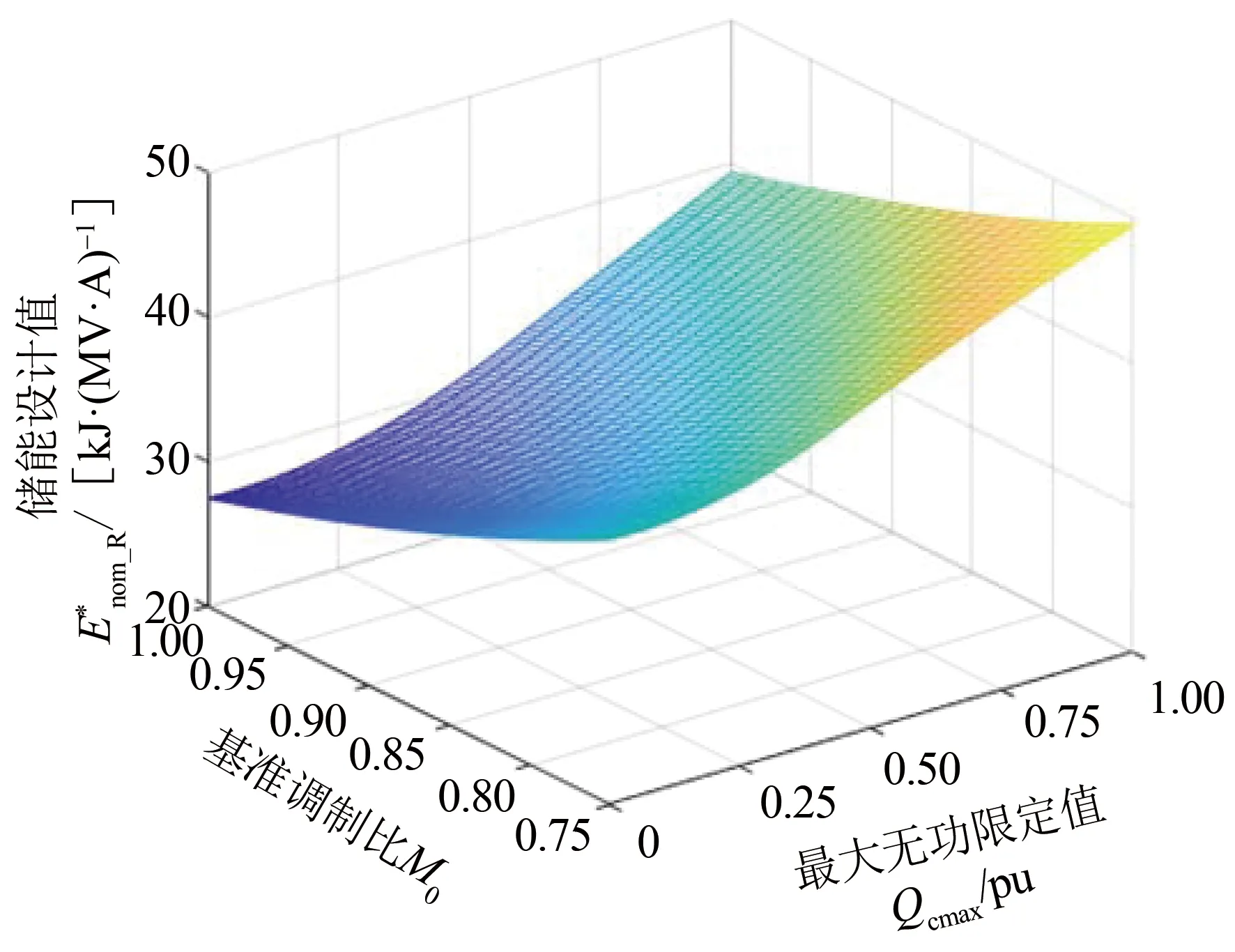
图9 MMC额定储能设计值随M0和Qcmax变化的三维曲线Fig.9 3-D Curve of the designed rated value of theenergy storage requirement varying with the base modulation index and maximum allowable reactive power

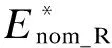
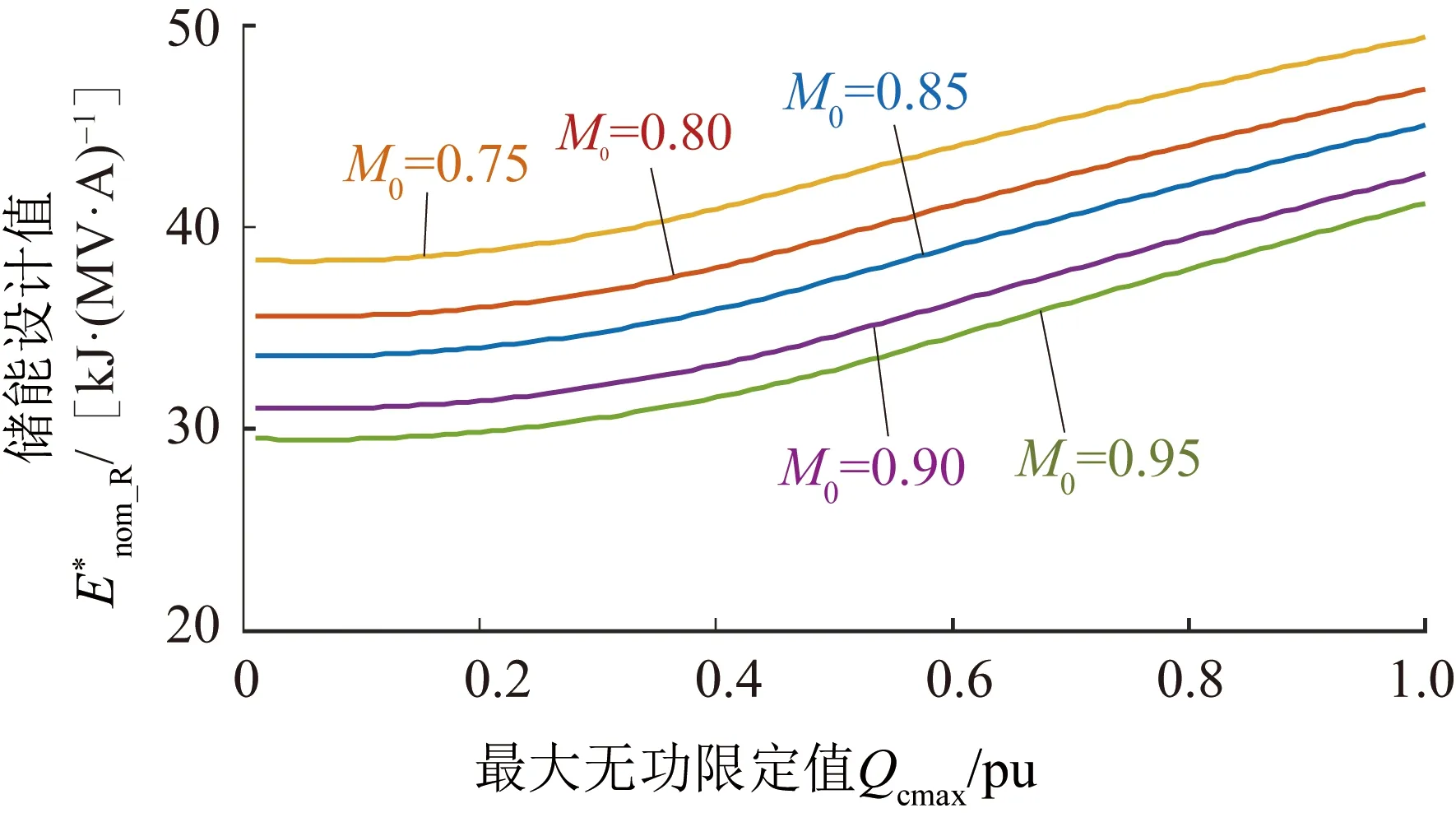
图10 几种典型基准调制比下的MMC额定储能设计值随Qcmax变化的曲线Fig.10 Curves of the designed rated value of the energy storage requirement varying with the maximum allowable reactive power under several typical modulation indices

基准调制比M0越高，MMC额定储能设计值越低。如图10中曲线所示，在最大容性无功限值为0.5 pu的情况下，当M0设计为0.75时，所需的额定储能设计值为42.59 kJ/(MV·A)。如果将M0分别提高到0.8和0.85，额定储能设计值将分别变为39.66 kJ/(MV·A)和37.06 kJ/(MV·A)，与M0=0.75的情况相比将分别下降6.88%和12.98%，这表明在保证MMC输出电压能力及其裕量的前提下，在设计交、直流额定电压时尽可能选择更大的基准调制比。

本文的分析是建立在标幺值参数模型和归一化的单位容量额定储能值上的，对于额定储能值的变化规律及其数值范围的分析适用于不同额定参数的MMC。基准调制比和功率输出范围将对MMC电容用量产生较为显著的影响。应根据所连接交流系统的需要选择适当的容性无功输出范围，并在满足电压输出能力及其裕度的前提下尽可能选择更高的基准调制比。

2.4 与实际工程参数的对比分析

本文选取了已投运的鲁西直流背靠背工程云南侧MMC和乌东德特高压混合直流工程龙门站MMC[23-24]，对其中的单位容量储能设计值进行分析，并与本文方法的计算结果进行对比，主要的工程参数如表1所示。乌东德特高压混合直流工程中包括一个±800 kV/5 000 MW的MMC和一个±800 kV/3 000 MW的MMC，两个MMC的子模块电压和数量相同，只是电容值按照各自容量比例设计，单位容量储能值完全一致，因此本文只选取了其中的±800 kV/5 000 MW的MMC进行分析。另外，每个±800 kV/5 000 MW的MMC实际上是由4个400 kV/1 250 MW的MMC单元串联构成的，因此表1中给出的是每个400 kV/1 250 MW的MMC单元的参数。另外需要注意的是，乌东德工程中MMC的基准调制比达到了0.99，这是由于该工程采用了全桥子模块和半桥子模块混合的MMC，通过全桥子模块负电平适当提高了MMC可实现的最大调制比[6-7]。由于采用了负电平利用，子模块电压、桥臂级联子模块数目和直流电压之间的相对关系也与常规MMC略有不同。

在表1中，按照MMC的实际工程参数计算出了单位容量储能设计值的工程参数。另一方面，也根据实际的基准调制比和最大容性无功输出限值等参数按本文方法计算出了单位容量储能设计值理论范围(Qcmax从0到1变化时单位容量储能设计值的变化范围)，可以看出实际工程中的单位容量储能值参数与本文的分析范围相符。另外，也根据表1中最大容性无功值计算出单位容量储能设计值的理论计算值。表1中单位容量储能值实际工程参数都接近但略大于理论计算值。应该注意到，表1中所列出的是典型工程中已选用的参数，但并不代表这些参数已经是最优参数。另外，电容电压波动只是电容用量选择的关键因素之一，实际工程设计可能还会考虑到其他的约束条件，并且通常会考虑到一定的安全裕量。因此，理论计算结果接近但略低于已有实际工程参数也是合理性，也说明已有工程在电容用量设计上仍有优化空间。

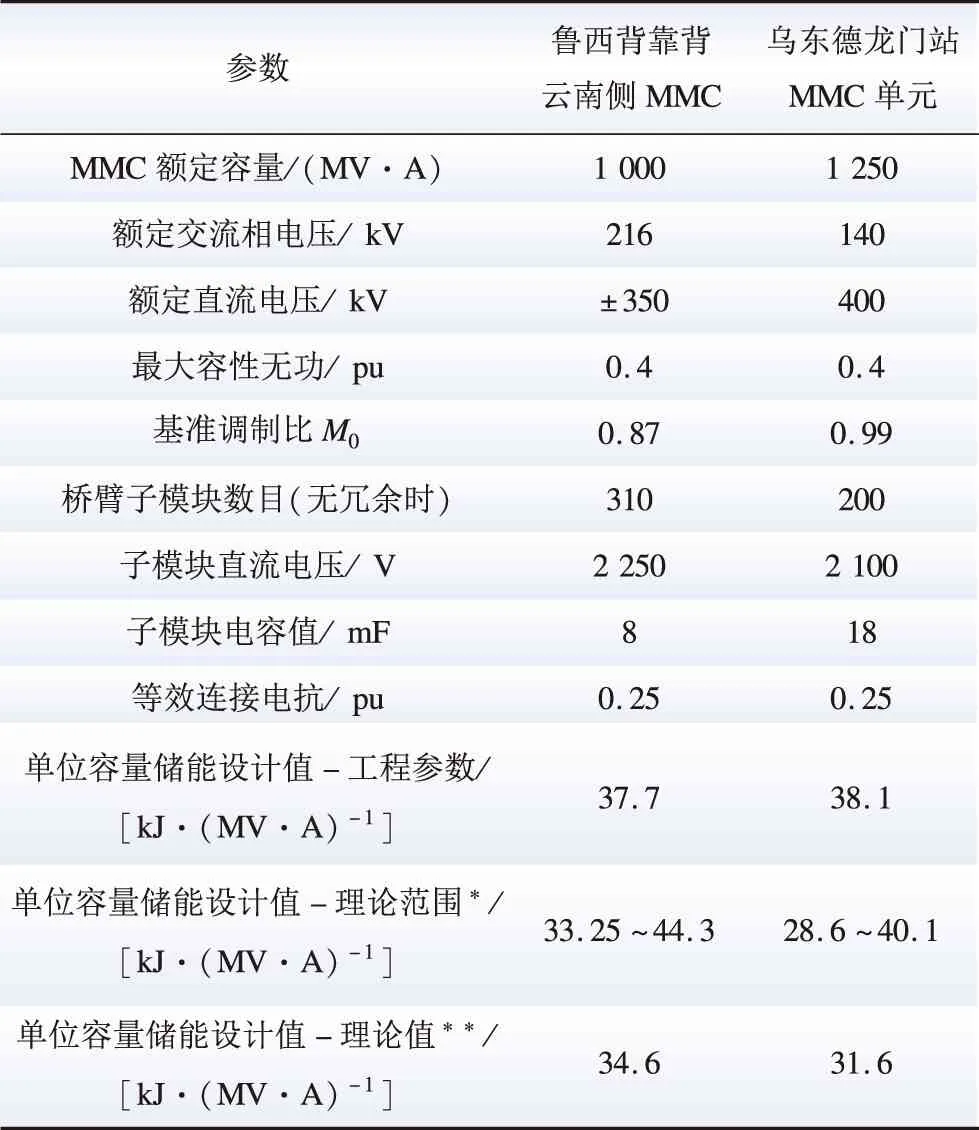
表1 典型工程的关键参数Table 1 Key parameters of the typical projects

3 仿真研究

参照表1中乌东德工程400 kV / 1 250 MV·A的MMC单元，在PSCAD/EMTDC中建立了仿真模型进行仿真研究，MMC的主要参数如表2所示。由于基准调制比达到了0.99，因此仿真模型中与实际工程类似，采用了混合MMC并利用全桥子模块负电平输出适当提高可实现的最大调制比。在仿真研究中，桥臂二倍频环流一直被控制为0。

表2 仿真模型的关键参数Table 2 Key parameters of the simulation model

1)额定功率圆模式的仿真验证。

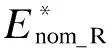
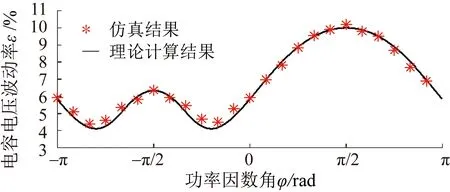
图11 电容电压波动率理论结果和仿真结果对比Fig.11 Comparison of the simulated and analytically calculated results for the capacitor voltage fluctuation rate

图12给出了功率因数角φ在-π/2、0、π/2和π等几种典型工况下的电容电压波动仿真波形，这几种工况分别对应额定感性无功功率、额定逆变有功功率、额定容性无功功率和额定整流有功功率等几种工况。从图12也可以看出，在φ=π/2(即额定容性无功功率)时电容电压波动峰值达到最大，且恰为所设计的波动率限值(10%)。

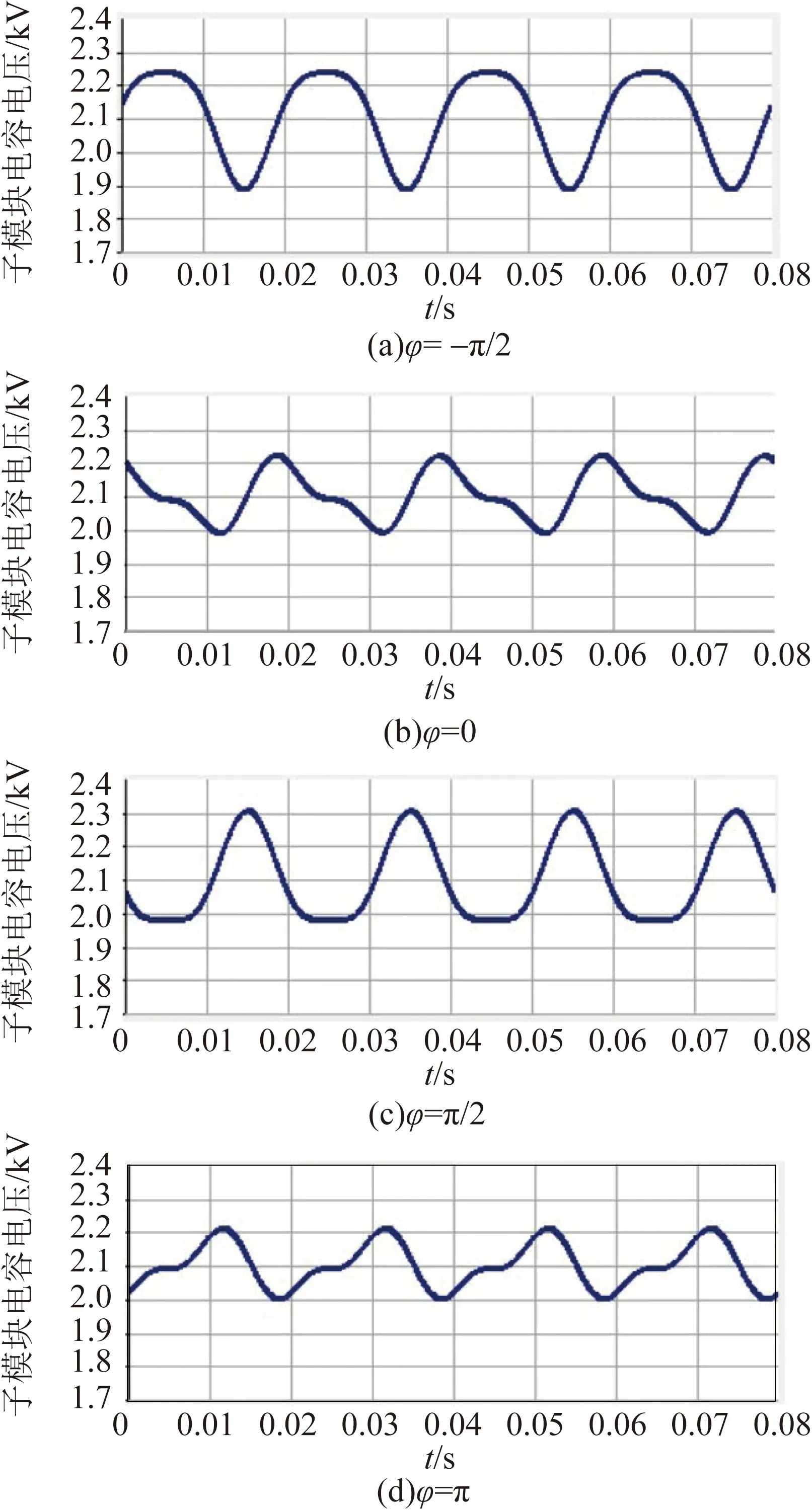
图12 几种典型工况下的电容电压波动仿真波形Fig.12 Simulated waveforms of the capacitor voltage for several typical operating conditions

2)最大容性无功限定模式的仿真验证。

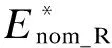
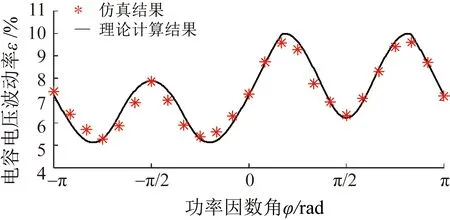
图13 最大无功限定模式下的电容电压波动率的理论计算结果和仿真结果的对比Fig.13 Comparison of the simulated and analytically calculated results for the capacitor voltage fluctuation rate when limiting the maximum reactive power

4 物理试验

本文还通过小容量MMC物理样机试验对所提出的MMC额定储能值计算方法进行了验证。MMC物理样机的主要参数如表3所示。由于在物理试验样机难以灵活调整子模块电容值，因此在物理试验中将子模块电容值固定，在设定的功率因数角φ的工况下，逐步增加MMC输出的视在功率，直至电容电压波动率达到设定值，并将此时MMC输出的视在功率作为额定容量SN。然后采用式(28)计算此运行工况所对应MMC单位容量储能值，并与第2节的理论分析结果进行对比。

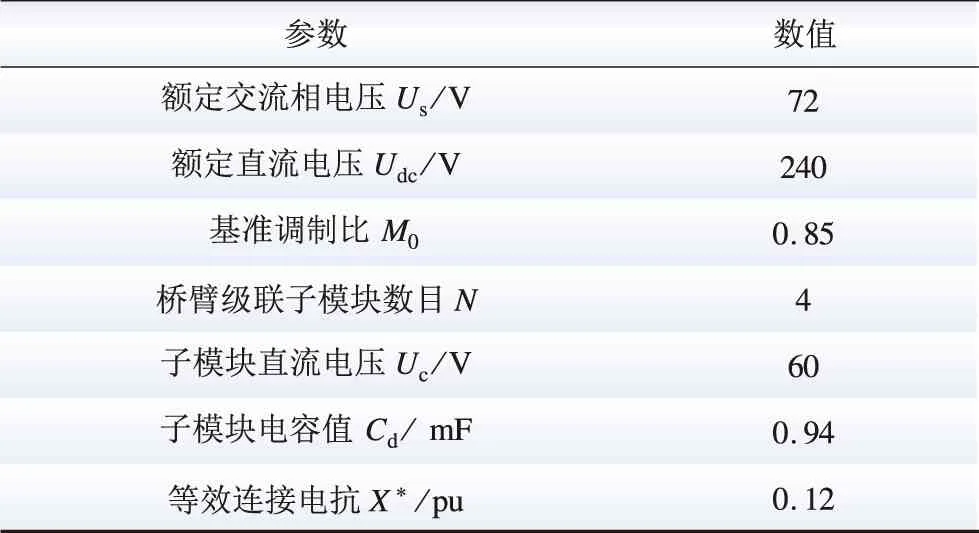
表3 物理试验样机关键参数Table 3 Key parameters of the experimental prototype

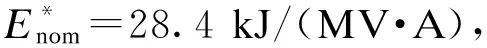
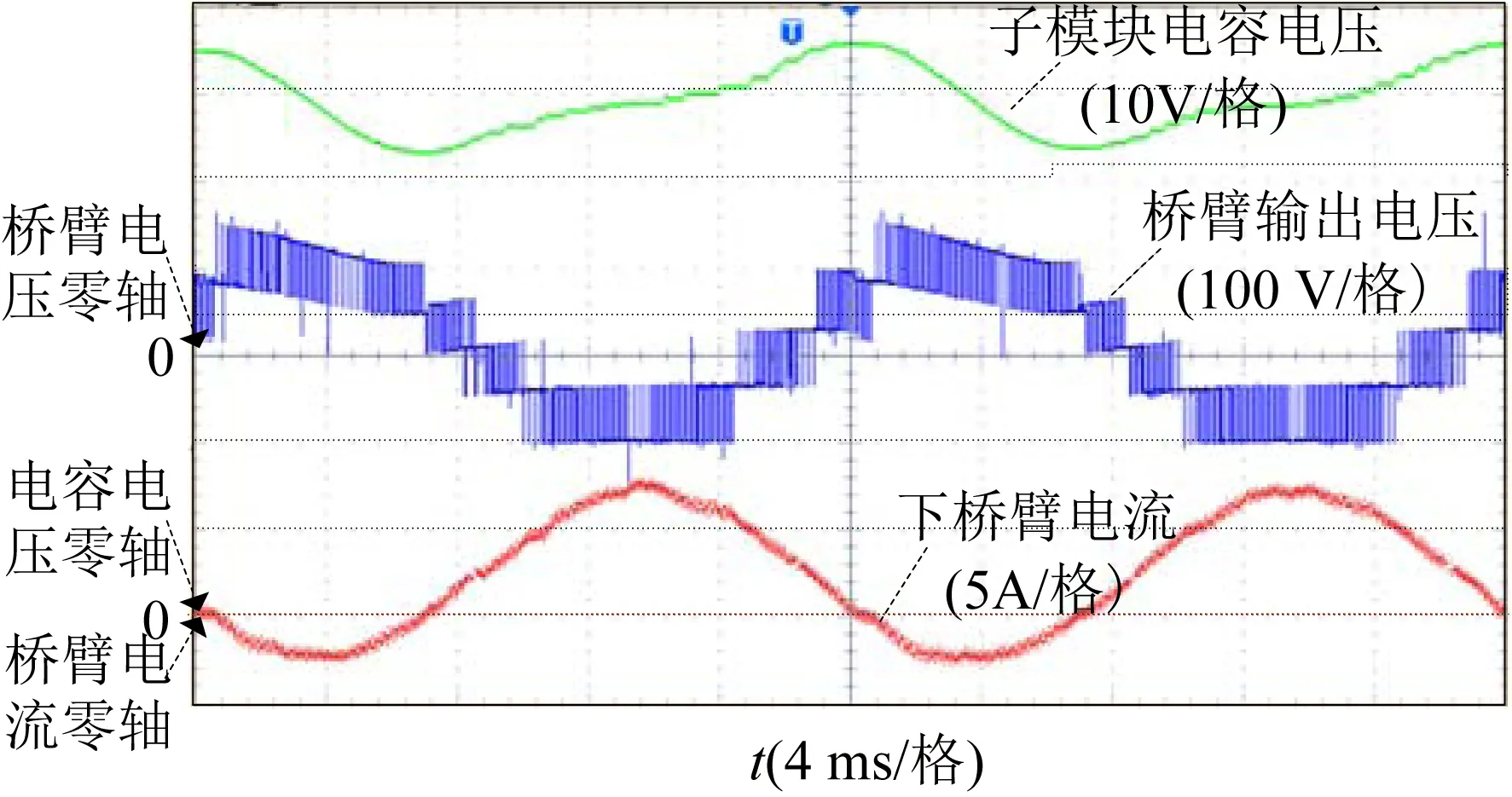
图14 φ=0工况的物理试验结果Fig.14 The experimental waveforms when φ=0

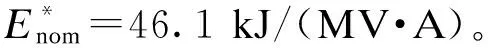
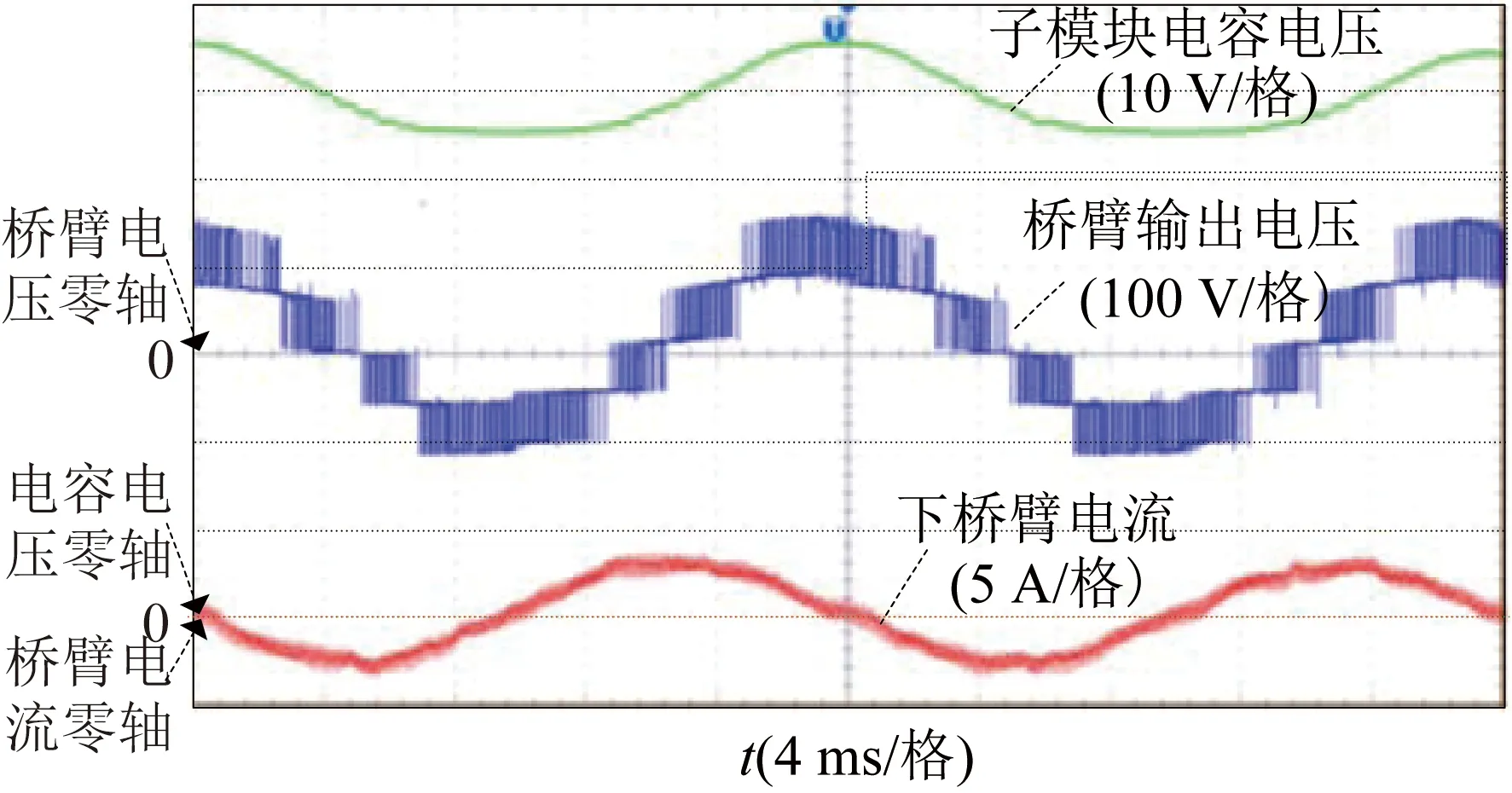
图15 φ=π/2工况的物理试验结果 Fig.15 The experimental waveforms when φ=π/2

5 结 论

本文以MMC单位容量额定储能值作为MMC电容用量的统一衡量与设计指标，建立了直接描述MMC额定储能需求值与电容电压波动率之间关系的标幺化计算模型。与以子模块电容值为设计指标的方法相比，所提方法直接将MMC额定储能值作为计算目标，并基于标幺化模型进行计算，可以避免多种参数对计算结果的影响，使MMC额定储能值设计只与基准调制比和输出功率范围相关，使不同额定参数MMC的电容用量的衡量、计算和分析可以得到统一和简化。基于所提出的额定储能值标幺化计算模型，对MMC额定储能设计值随基准调制比和功率输出范围的变化进行了详细的分析。分析结果表明，在基准调制比一定的情况下，MMC额定储能设计值主要由所需输出的最大容性无功范围决定，在满足所连接交流电网对无功输出的需求前提下，合理选择最大容性无功输出范围对MMC电容用量优化具有显著作用。例如，当基准调制比为0.85，等效连接电抗为0.2 pu时，随着最大容性无功输出范围标幺值从0到1变化，所需的MMC额定储能设计值约在33.1 kJ/(MV·A)到44.7 kJ/(MV·A)范围内变化。在最大容性无功输出范围确定的情况下，在保证MMC输出电压裕量的前提下，提高基准调制比将对降低电容用量具有明显的作用。这为MMC电容用量的设计和优化提供了明确的依据。数字仿真和物理试验结果验证了所提方法的正确性。