基于空调负荷数据挖掘的配电网扩展规划方法

苏宁，李笑彤，梁惠施，贡晓旭，吕风波，席嫣娜，齐步洋

(1.国网北京市电力公司经济技术研究院，北京市 100055；2.清华四川能源互联网研究院，成都市 610213；3.清华大学电机工程与应用电子技术系，北京市 100084)

0 引 言

近年来，电力大数据研究逐步深入，数据挖掘在优化配电网投资成本、提高电网设施利用效率领域得到广泛应用[1]。在智能电表推广普及条件下，用户侧具备海量的数据资源，其价值正逐步得到学术界及行业关注，在电力生产、传输、消费各环节领域得到了深入研究和应用[2-3]。

柔性可控负荷占比逐步提高对配电网规划影响越来越大，随着生活水平不断提高，夏季空调负荷占比越来越大，2020年北京电网夏季最大负荷时刻空调负荷占比达到41.96%。同时，空调类温控负荷具有典型季节特性且与日常环境温度变化有很强的相关性，能够通过数据分析的方法挖掘其调节潜力，有效指导配电网规划工作。配电网通常依据最大负荷开展规划，但实际中空调负荷具备一定可调节潜力，可在规划中挖掘空调负荷需求侧响应(demand response，DR)潜力，实现整体效益最优。电力需求侧响应是指通过优化用电方式，在完成用电功能的同时减少电量消耗和电力需求，实现低成本电力服务所进行的用电管理活动[4-5]。负荷数据对需求响应潜力挖掘具有重要意义[6]，文献[7]提出融合多种算法的综合聚类方法对用户负荷特性及可调节潜力进行分析，证明了通过用户数据挖掘可调节潜力具有可行性；文献[8]以用户心理学原理为基础，通过考虑峰谷分时电价调节构建用户调节潜力指标，通过该指标对负荷进行聚类，为通过电价引导用户用电行为奠定基础。但目前大量文献重点围绕负荷聚类算法开展研究与优化，较少通过融合负荷数据挖掘与用电设备物理特性开展响应潜力研究。相关学术和实践证明，通过对用户侧空调负荷进行直接负荷控制来削减负荷是一种有效的需求响应手段[9]。空调负荷主要集中在夏季用电高峰期，具有时间短、比重大、峰值高的特点[10]，同时建筑具有一定冷能存储能力，空调负荷被切断或调低功率一段时间不影响用户使用舒适度[11]。当前，一些研究在配电网规划中考虑了用户侧需求响应资源[12-15]，以延缓配电网建设投资。但大多数都是基于经验设定需求侧响应上限[16-19]，缺乏实际数据的支撑，难以反映实际情况，会给规划和运行策略分析带来误差。

因此，通过用户空调负荷实际数据挖掘，准确评估用户的需求响应潜力对于优化配电网规划方案具有重要意义，本文基于用户实际负荷数据，结合外部环境温度影响，建立空调数据挖掘模型，通过聚合用户负荷及空调物理特性研究需求响应潜力评估方法，基于评估结果，构建配电网扩展规划模型并进行求解，最后通过IEEE 33节点配电网算例对模型进行验证。

1 负荷数据挖掘模型及方法

1.1 空调数据挖掘模型

根据建筑负荷温度响应相关研究[20-21]，建筑负荷与室外温度呈近似分段线性关系，如图1所示。

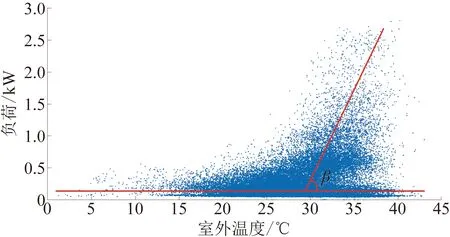
图1 建筑负荷温度响应散点图Fig.1 Scatter point of load temperature response

因此，可利用建筑负荷与室外温度的线性关系来识别空调运行状态和温度响应相关参数。从用户负

荷数据中分离出空调负荷属于盲源分离问题，但由于空调负荷与室外温度存在线性关系，而洗衣机、冰箱等其他负荷与室外温度无关联性，因此，可将室外温度作为对空调负荷的估算依据，将空调负荷进行分离。本文采用基于隐马尔科夫模型的算法，从用户负荷历史数据中评估出单个用户空调的温度响应斜率、空调的状态量(开关状态和设定温度)以及非空调负荷的状态量，进而重建空调负荷历史曲线。分离出空调负荷历史曲线之后，就可以对用户的需求响应潜力进行评估。

利用建筑负荷与室外温度的线性关系来识别空调运行状态和温度，如下所示：

Pc(t)=β·max[Tc(t)-Tset,0]+Pbase(t)+εα(t)

(1)

式中：Pc(t)表示与温度有关的空调负荷与非空调负荷之和；Tc(t)表示t时刻室外温度；Tset表示空调室内设定温度；β表示空调的温度响应斜率；Pbase(t)表示用户非空调负荷，该负荷与温度线性相关性低；εα(t)为随机变量噪声，服从正态分布。

相关研究表明，当用户不使用空调时，建筑负荷与室外温度间仍存在一定程度的线性相关性，如果直接对智能电表数据和室外温度进行线性回归，将高估空调的温度响应斜率。因此，为消除非空调负荷对空调负荷温度响应参数干扰，应用迭代方法先从智能电表数据中将空调负荷与非空调负荷分量大致分离，然后再将分离得到的空调负荷分量对室外温度进行线性回归。

比较使用空调和不使用空调的典型日负荷曲线，前者减去后者得到初步估计的空调负荷曲线。假设不使用空调的日负荷为Pbase,0(t)，使用空调的典型日负荷为P1(t)，典型日空调负荷分量可用式(2)估计。

Q1(t)=P1(t)-Pbase,0(t)+ε(t)

(2)

式中：ε(t)是由难以预测的非空调负荷使用变化所带来的随机误差量，假设非空调负荷具有相同的概率分布，故ε(t)仅影响回归结果的标准方差，不会对回归系数产生系统性误差；Q1(t)表示初步估计的空调负荷。

为识别空调在不同时段内的开关状态，引入二值状态量I(t)，I(t)=1表示空调处于开启状态，I(t)=0表示空调处于关闭状态。因此，空调负荷温度响应方程可用下式表示：

(3)

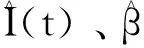
步骤1：对所有开关状态初始化I(t)=1；

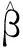
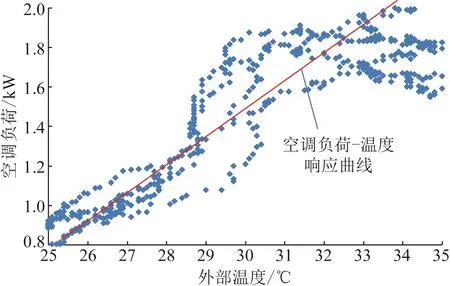
图2 空调负荷-温度响应曲线Fig.2 Response slope of air-conditioning load corresponding to temperature

步骤3：计算每个数据点到所拟合直线l间的欧几里得垂直距离，对到直线l距离小于到x轴(室外温度)距离数据点，更新I(t)=1；对到直线l距离大于等于到x轴(室外温度)距离的数据点，更新I(t)=0；

1.2 聚合负荷的需求响应潜力评估

通过聚合用户空调可控负荷，可将需求响应资源纳入配电系统规划边界条件，通过智能系统控制空调运行状态，有效降低电网投资成本。假设控制程序将空调设定温度变为目标温度Ts，用户k需求响应潜力可用下式表示：

(4)

(5)

在规划问题中，聚合负荷需求响应潜力评估主要目的是通过数据挖掘较为准确地确定可控负荷边界。

2 配电网扩展规划模型

2.1 规划框架

通过挖掘电表历史数据，可以发掘用户的空调可控负荷潜力边界，降低配电网扩展投资成本，基于上述方法构建基于负荷数据挖掘的配电网扩展规划框架，如图3所示。

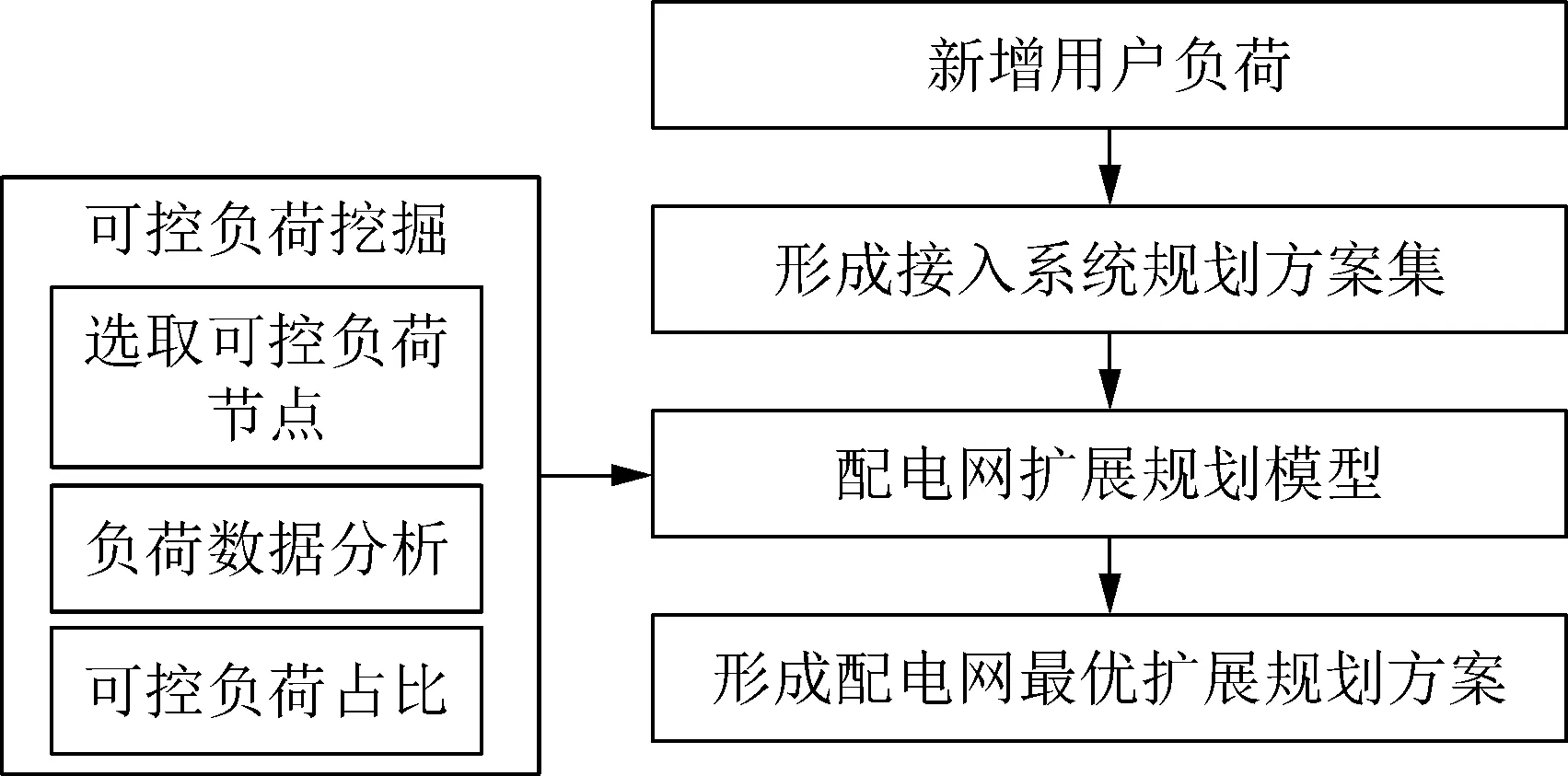
图3 优化扩展规划框架Fig.3 Collaborative planning framework

2.2 目标函数

为简化模型，更加贴近工程实际需求，在新增负荷待接入配电网场景中，期望通过需求侧响应降低配电网投资及运行成本。因此，以折算到年的配电网扩展投资成本及需求侧响应补偿成本之和最小为目标函数，具体如式(6)所示：

minCcost=C1+C2

(6)

式中：Ccost表示配电网折算到年的总成本，万元；C1为折算到年的配电系统扩展规划初始投资成本，万元；C2为折算到年的可控负荷需求响应的补偿费用成本，万元。

考虑新增负荷接入已有配电网，将相关设备及线路总投资折算到单位长度投资中，并且将配电网全寿命周期成本折算到年成本，可由式(7)计算。

(7)

式中：ccost表示新增负荷接入系统单位线路长度造价，万元/km；Ll表示第l个新建线路长度，km；W表示待建线路的条数；δl表示第l条新建线路是否选中，δl=1表示选中第l条新建线路，δl=0表示未选中第l条新建线路；r表示贴现率；n为配电网运行生命周期，年。

考虑已有用户中的空调可中断负荷，其参与需求侧响应采用直接中断的方式，由配电网运营商提供补偿，则可中断负荷年补偿成本可用式(8)表示。

(8)

式中：Pcon.m表示第m个负荷所挖掘出的可控负荷，kW；Tcon.m表示第m个可控负荷年等效响应时间，h；p2表示可中断负荷参与需求响应补偿价格，元/(kW·h)；N1表示可控负荷节点个数。

2.3 约束条件

1)节点功率平衡。

配电系统各节点功率平衡应满足如下约束：

(9)

式中：Pi和Qi分别表示节点i的有功功率和无功功率；Ui和Uj分别表示节点i和节点j的电压幅值；Gij和Bij分别表示支路ij的电导和电纳；θij表示节点i和节点j的相角差。

2)支路潮流约束。

通常对配电网潮流计算进行简化，利用线路最大传输容量作为约束:

(10)

式中:Ωk表示支路k所带负荷节点的集合；Sk表示支路k的极限输送容量。

3)节点电压约束。

配电系统节点i的电压偏差需满足如下约束:

ΔUmin≤ΔUi≤ΔUmax

(11)

式中：ΔUmin表示允许电压偏差下限；ΔUmax表示允许电压偏差上限；ΔUi表示第i个接入点的电压偏差。

4)需求响应约束。

通过对用户负荷数据挖掘，得到空调可控负荷相应潜力，约束条件包括可中断负荷约束：

Pcon.m=λmPL.m

(12)

式中：PL.m表示第m个负荷；λm表示可中断负荷系数，满足式(13)：

λmmin≤λm≤λmmax

(13)

式中：λmmin表示第m个可中断负荷系数下限值，通常设置为所有用户都不参与响应，取λmmin=0；λmmax表示第m个可中断负荷系数上限值，可通过式(14)确定：

(14)

3 模型求解方法

3.1 假设条件

配电网规划通常采用预测最大负荷作为规划边界条件，考虑冬季运行方式下，不需要空调制冷，因而用户负荷数据无法识别空调响应潜力，本文算例假设最大负荷出现在最热月份，且最热月空调开启最多，数据分析价值更明显。考虑规划问题所考虑的尖峰负荷持续时间较短，并且建筑物存在一定热惯性，用户能获得一定的补偿，部分用户有意愿参与需求侧响应。针对本场景在模型求解过程中做如下假设：

1)选取夏季最热月最大负荷日各个时刻及春秋典型日所对应负荷及环境温度作为基础数据；

2)忽略由难以预测的非空调负荷使用变化所带来的随机误差量ε(tmax)；

3)假设负荷最大所对应时刻为tmax。

3.2 求解步骤

1)用户群需求响应潜力评估。

假定配电网中节点i所带用户群数量为Ni，各用户需求响应潜力评估步骤如下所示：

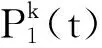
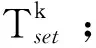
步骤3：重复步骤2得到Ni个用户的空调负荷温度响应斜率及设定温度，在负荷最大时刻的温度设定目标为T(tmax)，计算用户群Ni的需求响应潜力比例可得到可控负荷上限值，如式(15)所示:

(15)

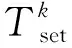
2)扩展规划模型求解。

步骤1：待接入系统负荷数为M，待接入负荷节点j所对应的规划方案数为Wj，则系统总扩展规划场景数B如式(16)所示：

(16)

步骤2：在此边界条件下，针对各个规划场景集，以系统总成本最小为目标函数，考虑式(9)—(13)约束条件，应用粒子群算法，对每个场景进行求解，得到总成本最小的规划方案。粒子群算法不再赘述。

4 算例分析

4.1 算例简介

为了验证本文模型和方法的正确性和有效性，以IEEE 33节点配电网为例进行验证，如图4所示。设定10 kV配电网扩展规划场景，其最大负荷出现在夏季，已有负荷节点负荷增长已基本饱和，对其节点功率做适当调整，采用前推回代法进行潮流计算。

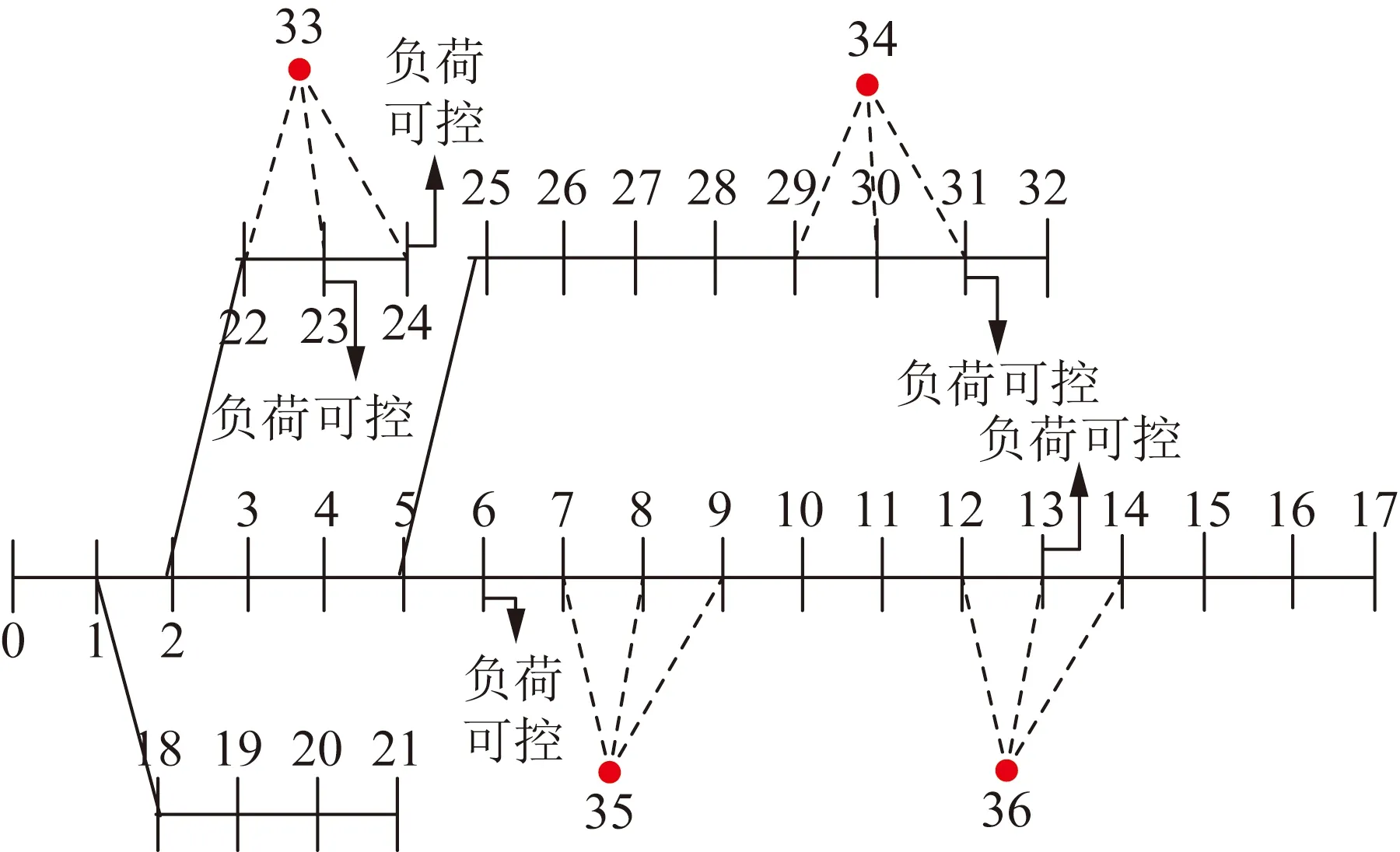
图4 IEEE 33节点配电网算例Fig.4 IEEE 33-node distribution network example

4.2 参数设定

在该规划场景下，新增待接入负荷节点为节点33、34、35、36，新增负荷容量按照未来饱和负荷预测值进行考虑，每个新增负荷有3种接入方案，假设均采用架空线路方式接入，导线型号相同，线路单位长度投资统一采用25万元/km[22]。各负荷接入方案对应的线路长度及参数如表1所示。

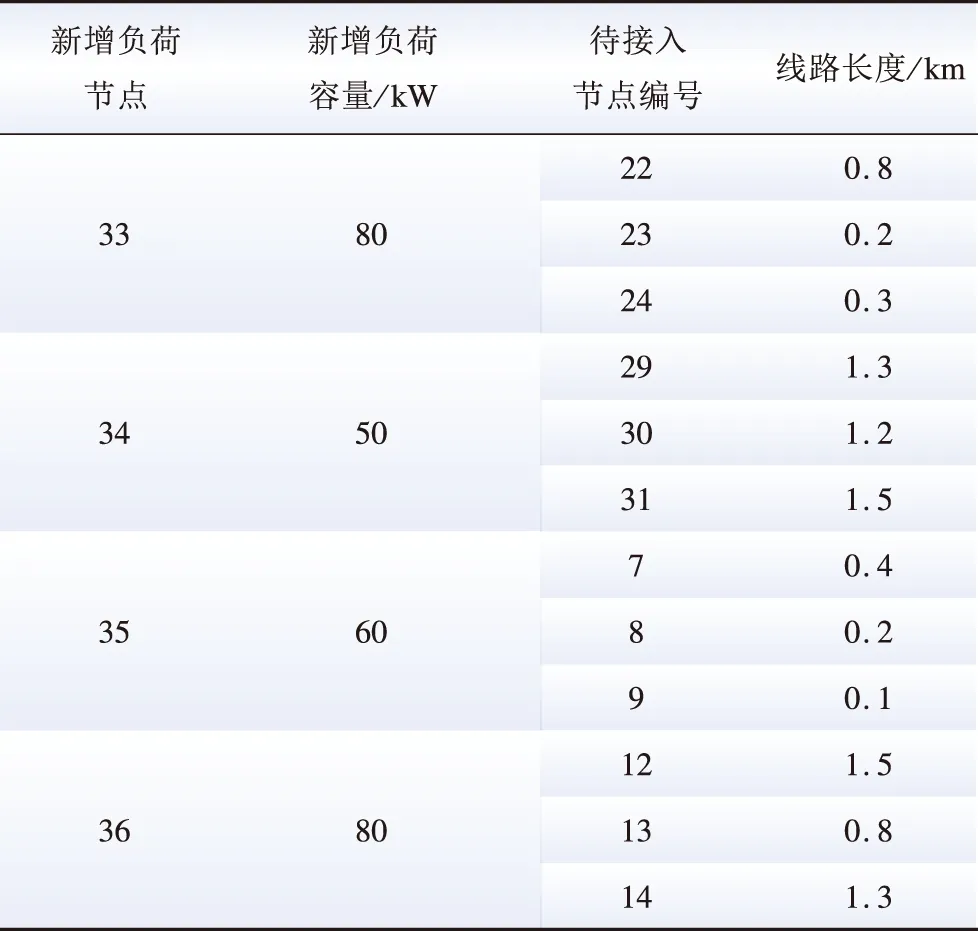
表1 新增负荷扩展规划方案Table 1 Planning scheme of new load expansion

可参与需求侧响应的节点分别为节点6、13、23、24、31，其节点所带用户群可通过负荷数据挖掘分离出空调可控负荷来参与需求侧响应。其中，以节点6为例，其所带用户数量为50，已取得最大负荷数据，假设为可中断负荷，年参与需求侧响应时间为200 h，用户可以获得可中断负荷补贴为0.4元/(kW·h)[14]。

4.3 分析场景

以节点6所带某用户负荷数据为例，选取其8月23日与4月5日负荷数据进行分析，最大负荷时刻点气温为35 ℃，利用上述方法分析其空调负荷温度响应斜率。根据概率分布情况，节点6某用户空调负荷温度响应斜率为0.13 kW/℃，对该节点所有用户进行分析，得到其响应斜率概率分布，如图5所示。

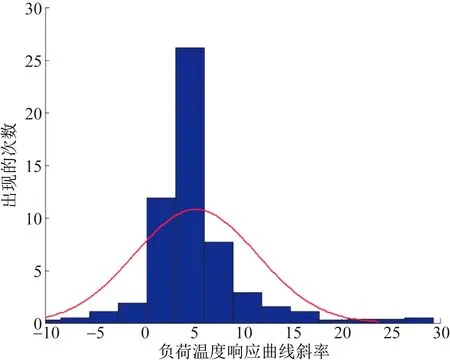
图5 响应斜率概率分布Fig.5 Probability distribution of response slope

场景1：以所有用户斜率均值进行分析，最大负荷时刻点温度为35 ℃，空调设定温度为26 ℃，假设有一半用户参与响应，则估计该节点空调负荷为23.94 kW，该节点响应比例为19.97%，且假设节点6、13、23、24、31分别参与需求侧响应的可中断负荷比例上限均为19.97%。

场景2：基于全量数据开展挖掘，针对各个节点分别计算每个用户的负荷温度响应斜率及各个用户的设定温度，最大负荷时刻点温度为35 ℃，空调目标设定温度取26 ℃，通过式(14)计算得到节点6、13、23、24、31分别参与需求侧响应的可中断负荷比例上限分别为18.52%、21.63%、19.56%、23.12%、18.97%。

场景3：不考虑用户空调负荷参与需求侧响应，忽略可控负荷需求响应的补偿费用成本，仅以配电系统扩展规划初始投资成本作为目标函数，进行规划方案选择和制定。

4.4 结果分析

按照上述场景，在上述输入边界条件下，应用粒子群算法，求解得到各个方案总成本最小规划方案，其中，场景2折算到年的总成本最小(4.629 1万元)，为最优规划方案，网架规划结果如图6所示。

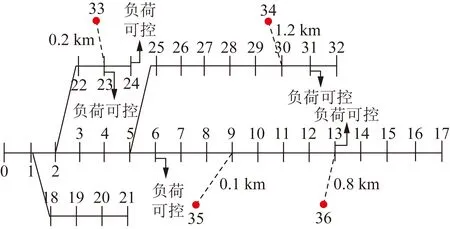
图6 最佳规划方案(场景2)Fig.6 The best planning scheme (case2)

场景1最佳规划方案年总成本为5.246 8万元，场景3最佳规划方案年总成本为6.321 6万元，可见，通过计算全量数据挖掘需求响应潜力的场景2规划方案的系统总成本最小，对比结果如表2所示。

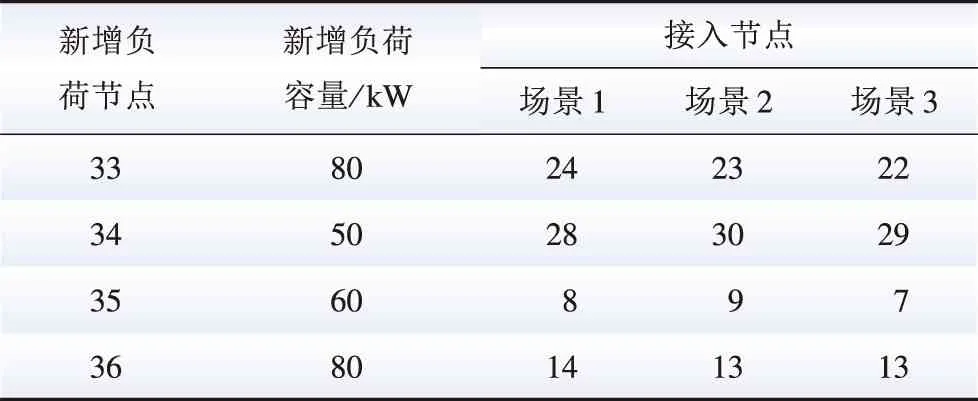
表2 规划方案对比Table 2 Planning scheme comparison

最优方案下，在需求侧响应比例上限约束下，优化得到场景2最优规划方案的各节点参与需求侧响应的实际负荷占比，如表3所示。

表3 各节点参与需求侧响应的负荷占比Table 3 Interruptible load factor of air-conditioning at each node

根据仿真结果可见，通过全量用户数据挖掘，考虑其需求侧响应潜力，使得原有配电网供电能力显著增加，用户通过参与需求侧响应可显著降低配电网投资成本。以新增负荷节点33为例，在不考虑需求侧响应情况下，其接入节点23、24时，线路较短投资较小，但根据潮流计算结果，在此条件下节点23、24电压分别降为0.856 6 pu、0.902 3 pu，远低于国家标准规定的-7%下限，因此，只能接入较远的节点22。当考虑节点23用户群参与需求侧响应后，负荷接入后其电压偏差满足要求，此时线路长度大大缩短，考虑需求侧响应补偿后总成本仍然较低。

在场景2最优规划方案下，分别设置不同上限需求侧响应比例，求解各条件下的最佳适应度值，即系统总成本，如图7所示。可见，随着需求侧响应上限参数增加，最佳适应度值也在增加，但随着上限增加到一定程度，其对于系统总成本下降的边际效益逐步递减，主要是由于上限越高，需要付出的需求侧响应补偿费用越大。由此可见，通过用户数据挖掘获得合理的需求侧响应限值对于配电网规划具有十分重要的现实意义。

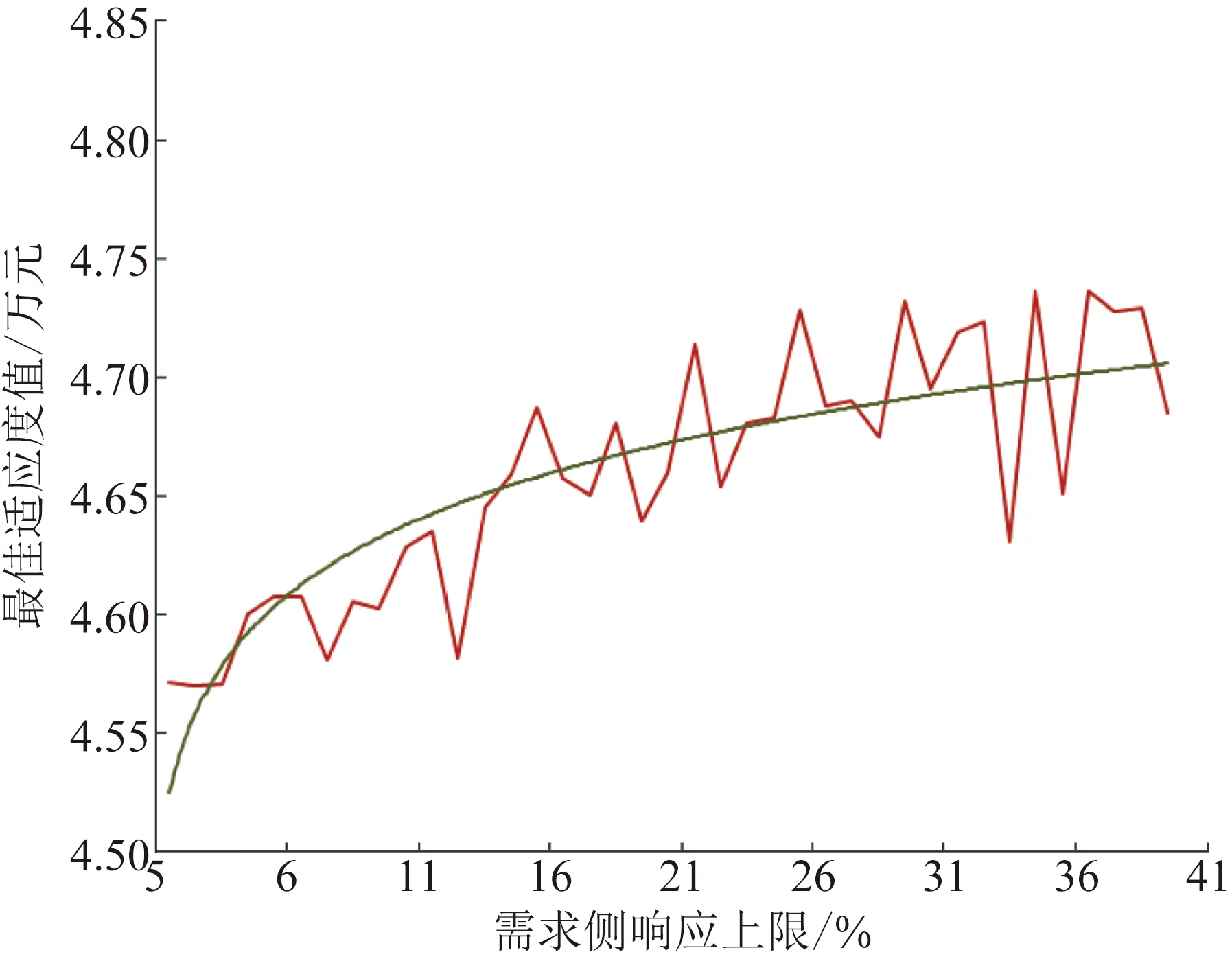
图7 总成本与需求侧响应上限关系Fig.7 Relationship between total cost and demand response upper-limit

5 结 论

本文针对配电网规划领域负荷数据挖掘问题开展深入研究。首先，基于实际数据分析，考虑用户空调、冰箱、洗衣机等众多家庭用电设备中，空调负荷与室外温度呈近似分段线性关系的特征，应用隐马尔科夫模型算法，建立空调负荷挖掘模型，将空调负荷从用户用电数据中分离。通过聚合用户群，考虑用户使用空调的概率分布，研究需求侧响应评估方法，考虑建筑物热惯性，利用电价补偿机制增强用户控制空调启停意愿，平衡用户经济成本与舒适度，实现对需求侧响应限值的准确计算。其次，以配电系统折算到年的总成本最小为目标函数，考虑潮流、电压、需求侧响应等约束条件，提出配电网扩展规划模型并进行求解。最后，采用IEEE 33节点算例对模型有效性进行验证，考虑需求侧响应后，最优规划方案年总成本为4.629 1万元，低于不考虑需求侧响应的总成本(6.321 6万元)。

本文的数据挖掘方法能够有效评估用户需求侧响应潜力，有利于优化配电网规划方案，降低系统总成本，延缓配电网扩展投资，提高配电系统整体经济性。本文提出思路和方法对于实际配电网规划工作具有重要的现实意义和作用。