风-光-火-抽蓄联合系统中抽水蓄能电站最佳容量配置

程孟增，唐一金，商文颖，满林坤，张南，张娜，李泓泽

(1. 国网辽宁省电力有限公司经济技术研究院，沈阳市 110015；2. 华北电力大学经济与管理学院，北京市 102206；3. 国网辽宁省电力有限公司检修分公司，沈阳市 110015)

0 引 言

在全球能源结构转型、环境问题日益严峻的大背景下[1-2]，大力发展风电、光伏是支撑“30·60”目标实现的有效途径之一。截至2020年底，我国风电装机2.8亿kW，光伏装机2.5亿kW，位居全球首位[3]。但伴随新能源的大规模并网，其间歇性、波动性、反调峰性，也给电力系统的稳定运行造成了极大的压力，电网需要更多的平衡电源容量[4-5]。抽水蓄能电站作为优质调节电源，能够有效改善大规模风电并网带来的反调峰特性，起到削峰填谷的作用[6-7]，在保证电力系统安全稳定运行的同时，对于最大限度实现新能源消纳具有不可或缺的作用。

现有文献针对含抽水蓄能电站的混合能源系统运行及容量配置已有大量研究。文献[8-11]从经济与环境角度把弃风电量、发电成本、污染物惩罚成本、弃电惩罚成本等最小作为目标，建立了含抽水蓄能的混合系统优化调度模型，并采用Yalmip工具箱、遗传算法、粒子群算法等进行求解，但上述文献未考虑抽蓄容量配置与调度运行优化策略之间的协调关系。

目前，对于抽水蓄能容量规划最常规的方法是以系统运行经济性、技术性和可靠性作为指标，配合常规机组平衡地区负荷峰谷差，通过评价或运行优化的方法，得出抽蓄容量配置。文献[12-14]通过选取容量效益、节煤效益、调峰容量比等经济性与技术性指标，采用主成分分析模型、贝叶斯模型、熵理论对不同容量的抽水蓄能电站进行评价，从而得出抽水蓄能电站的最佳容量配置。

以上研究仅考虑抽蓄与新能源互补，而实际系统中占比最大的是火电，也需要考虑抽蓄与常规机组配合。文献[15]基于双层规划理论，构建了光伏/小水电/抽水蓄能容量配置模型，上层以系统投资成本最小为目标，下层以售电收益最大为目标，但该文献主要针对火电比重较小的四川电网为研究对象，对我国其他大多数火电比重较大的电网，其参考借鉴价值有限。

针对上述文献的不足，本文从抽蓄容量配置与火电机组协调运行角度出发，构建抽水蓄能电站最佳容量配置双层规划模型。上层以最大限度减少弃风、弃光电量之和为目标确定抽水蓄能电站容量配置，下层基于上层容量配置，以追求经济效益和环境价值的最大化为目标，同时改善系统运行条件，采用基于Tent映射混沌优化的改进灰狼算法对目标函数进行求解，最终得到特定联合系统中抽水蓄能电站的最佳容量配置与基于典型日的调度运行优化结果。

1 双层规划模型构建

双层规划模型构建的基本思路如图1所示。上层为容量配置问题，为下层提供抽水蓄能电站容量的规划方案，下层为优化调度问题，通过最优功率分配，使得既定容量下的抽水蓄能电站实现联合系统在经济效益、环境价值和系统运行状况改善方面实现优化，同时将优化运行结果反馈给上层，检验在该运行策略下抽水蓄能电站的容量配置是否合理。

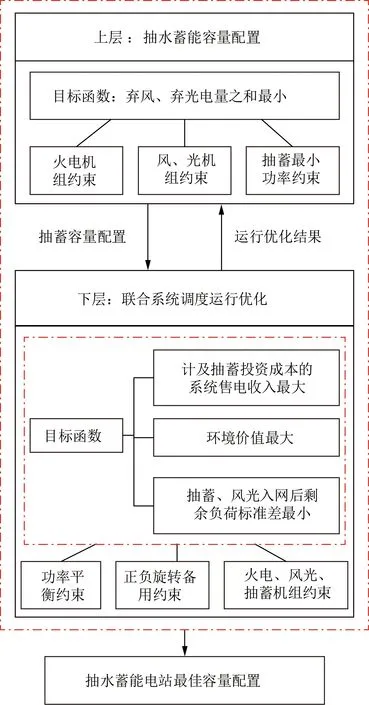
图1 双层优化模型结构Fig.1 Structure of the two-layer optimization model

1.1 上层优化模型

1.1.1 目标函数

上层优化模型的目标函数为联合系统中弃风、弃光电量之和最小，以此来确定系统所需抽水蓄能电站的容量配置。影响弃风、弃光电量之和的主要因素包括火电、风光运行约束等，具体表示为：

(1)

式中：Fq为弃风、弃光电量之和；T为一天的时长；Δt为优化时间尺度；Pw-q(t)、Ppv-q(t)分别为t时段弃风、弃光功率。

关于弃风电量的表征：当t时刻风资源的可用功率小于系统的风电装机容量时，弃风电量表征为t时刻的风电可用功率与风电机组实际出力之差乘以时长；而当t时刻风资源的可用功率大于系统的风电装机容量时，弃风电量表征为风电装机容量与t时刻实际出力之差乘以时长。光伏的弃光电量表征类似，因此弃风、弃光电量为：

(2)

(3)

式中：Pw-y(t)、Ppv-y(t)分别为t时段风电和光伏的可用功率预测值；Pw(t)、Ppv(t)分别为风电、光伏在t时段的实际出力；Pw-power、Ppv-power分别为风电、光伏的装机容量。

为最大化发挥抽水蓄能电站的调节作用，抽水蓄能电站在负荷低谷时满功率抽水，因此，在负荷低谷时抽水蓄能的抽水负荷也就是其容量配置，具体表示为：

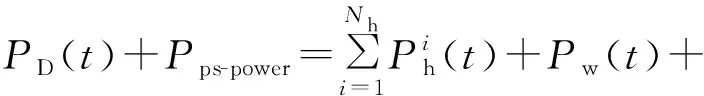
(4)

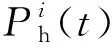
1.1.2 约束条件

1)火电机组约束。

出力约束为：

(5)

爬坡约束为：

(6)

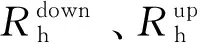
2)风电、光伏机组约束。

0≤Pw(t)≤Pw-power

(7)

0≤Ppv(t)≤Ppv-power

(8)

3)抽水蓄能最小功率约束。

在任一时刻t，抽水蓄能的装机容量应大于这一时刻的弃风、弃光功率，因此须满足最小功率约束：

Pps-power≥Pw-q(t)+Ppv-q(t)

(9)

1.2 下层优化模型

1.2.1 目标函数

下层优化目标是联合系统在上层给定的容量配置下，通过最优功率分配，来实现抽水蓄能电站对联合系统的优化调度，旨在最大化系统的经济效益与环境价值，并改善系统运行条件，影响下层目标的主要因素包括系统功率平衡约束，电量平衡约束，旋转备用约束，火电、风光机组、抽水蓄能的运行约束等。

1)联合系统经济效益。

联合系统经济效益以系统内各类主体发电利润之和最大化来表征，表示为：

maxFJJ=Fin-Fcost

(10)

式中：FJJ为联合系统的经济效益；Fin为系统发电收入；Fcost为系统运行成本。

联合系统中抽水蓄能电站容量占比越大，运行调度空间越大，但是其投资成本也就越大，若抽水蓄能电站未能在寿命周期内收回成本，就会降低抽水蓄能电站投资建厂的积极性，因此，本文把抽水蓄能电站的建造成本分摊到每日，加入抽水蓄能电站的日运行成本。抽水蓄能电站建造成本表示为：

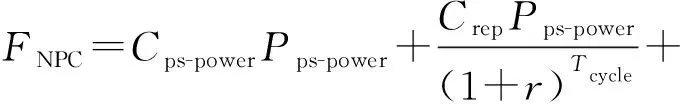
(11)

式中：FNPC为建造抽水蓄能电站的总成本；Cps-power为抽蓄电站装机容量的单价；Tcycle为抽蓄机组的全寿命周期；Crep为抽水蓄能机组的替换成本；r为折现率；Com-ps为抽水蓄能电站每年运行维护成本。本文为简化模型，假设上下水库建造成本折入抽蓄机组的单价。

在调度运行优化过程中，因固定成本对优化结果没有影响，因此除抽水蓄能机组外，其他机组的发电成本仅考虑其运行成本，火电机组运行成本主要为燃煤成本，为凸性非线性二次函数[16]；抽水蓄能机组运行成本为在负荷低谷时的抽水用电成本与每日分摊的建造成本，假设风电、光伏机组运行成本为0，系统运行成本具体表示为：

(12)

式中：Fcost-h为火电运行成本；Fcost-ps为抽水蓄能运行成本；ai、bi、ci为第i台火电机组的燃煤费用系数；St为t时段电价；τ为抽水蓄能机组的能量转换效率；Pps(t)为抽水蓄能机组在t时段的输出功率；ups表示抽水蓄能机组运行状态，1表示发电，-1表示抽水，0表示停运。

系统运行收入是指各主体售电收入之和与抽水蓄能机组调峰所得收入，表示为：

(13)

式中：Fin-h、Fin-w、Fin-pv、Fin-ps分别为火电、风电、光伏、抽水蓄能电站的售电收入；Sh、Sw、Spv分别为火电、风电、光伏平均上网电价；Stf为抽水蓄能电站参与调峰辅助服务的补偿标准。

2)环境价值。

环境价值是指消纳风、光、抽水蓄能等清洁能源替代火电机组发电产生的污染物减排所带来的价值，具体表示为：

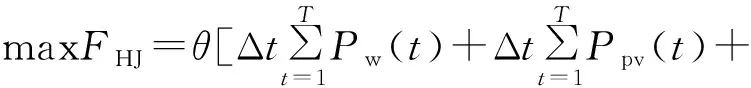
(14)

式中：FHJ为系统的环境价值；θ为单位电量煤耗；Cpf为单位污染物减排的价值，取365.9元/t[17]。

3)改善系统运行条件。

抽水蓄能电站既可发电进行削峰，也可抽水进行填谷，具有灵活的调节能力，很好地弥补了风电的反调峰特性，能够有效平滑联合系统的负荷曲线，改善系统运行条件。本文用抽蓄、风电、光伏入网后剩余负荷的标准差最小，作为改善系统运行条件的目标。

(15)

Prem(t)=PD(t)-Pw(t)-Ppv(t)-upsPps(t)

(16)

式中：σrem表征系统调度运行优化效果，具体以抽蓄、风电、光伏入网后剩余负荷的标准差来表示；Prem(t)为t时段的总负荷与风光、抽蓄出力之差。

1.2.2 约束条件

1)系统功率平衡约束。

(17)

2)电量平衡约束。

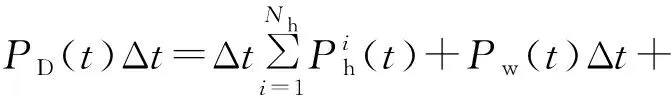
(18)

3)正负旋转备用约束。

由于风光出力具有随机波动性，且预测精度较低，因此，须预留备用以平衡预测值与实际出力的偏差。当出力不足时，弃风、弃光功率可重新投入使用，因此可作为正旋转备用，本文不考虑风光作为负旋转备用。

(19)

4)抽水蓄能机组约束。

出力约束为：

0≤Pps(t)≤Pps-power

(20)

能量平衡约束为：

(21)

水库库容约束为：

(22)

除满足上述约束条件外，还应满足火电、风电、光伏的运行约束，具体见式(5)—(8)。

2 双层规划模型的求解

本文建立了主从递阶关系的双层优化模型，上层模型为单目标多约束问题，下层为多目标多约束问题，非线性较强，本文采用基于Tent映射混沌优化的改进灰狼算法求解双层目标函数。在处理多目标问题时，粒子群算法、遗传算法等启发式算法得到了广泛应用[15,18-20]，但存在局部最优问题。灰狼优化(grey wolf optimizer，GWO)算法是一种新群体智能优化算法[21]，相较于其他启发式算法，具有参数设置简单、无导数机制和避免局部最优的优点。在该算法中，灰狼种群具有严格的社会等级制度，在金字塔顶端的称为α狼，是最合适的解决方案，第二和第三最佳解决方案被称为β狼和δ狼，其余候选解决方案称为γ狼，在GWO算法中，狩猎是由α狼引导β狼和δ狼，其余γ狼跟随这3只狼寻找全局最优解。

传统灰狼算法优化时的初始种群具有随机性，且分布不均匀，因此，可以利用混沌优化的遍历性、规律性优点，来改善种群的寻优搜索能力[20]。较为常见的混沌映射有Logistic映射与Tent映射，文献[21]证明了Tent映射比Logistic映射具有更强的遍历性，改进后的Tent映射为：

(23)

式中：xt为第t次迭代后灰狼所处位置。

(24)

式中：xmax,j和xmin,j分别为第j维变量的搜索上、下界。

(25)

在基于Tent映射混沌优化的改进灰狼算法获得Pareto前沿后，通过距离乌托邦点最短来确定最优解。乌托邦点假设所有目标同时最大化，由于目标函数之间存在折中关系，因此无法获得多目标的乌托邦点，但可以把单个目标的乌托邦点作为参考点，通过式(26)，其最小值作为折中最优解[22]。所有优化目标应用等效权重。

min‖Fpareto-Fu‖p

(26)

式中：Fpareto为帕累托最优解；Fu为乌托邦点；‖·‖p表示p范数。

基于Tent映射混沌优化的GWO算法的流程如图2所示。

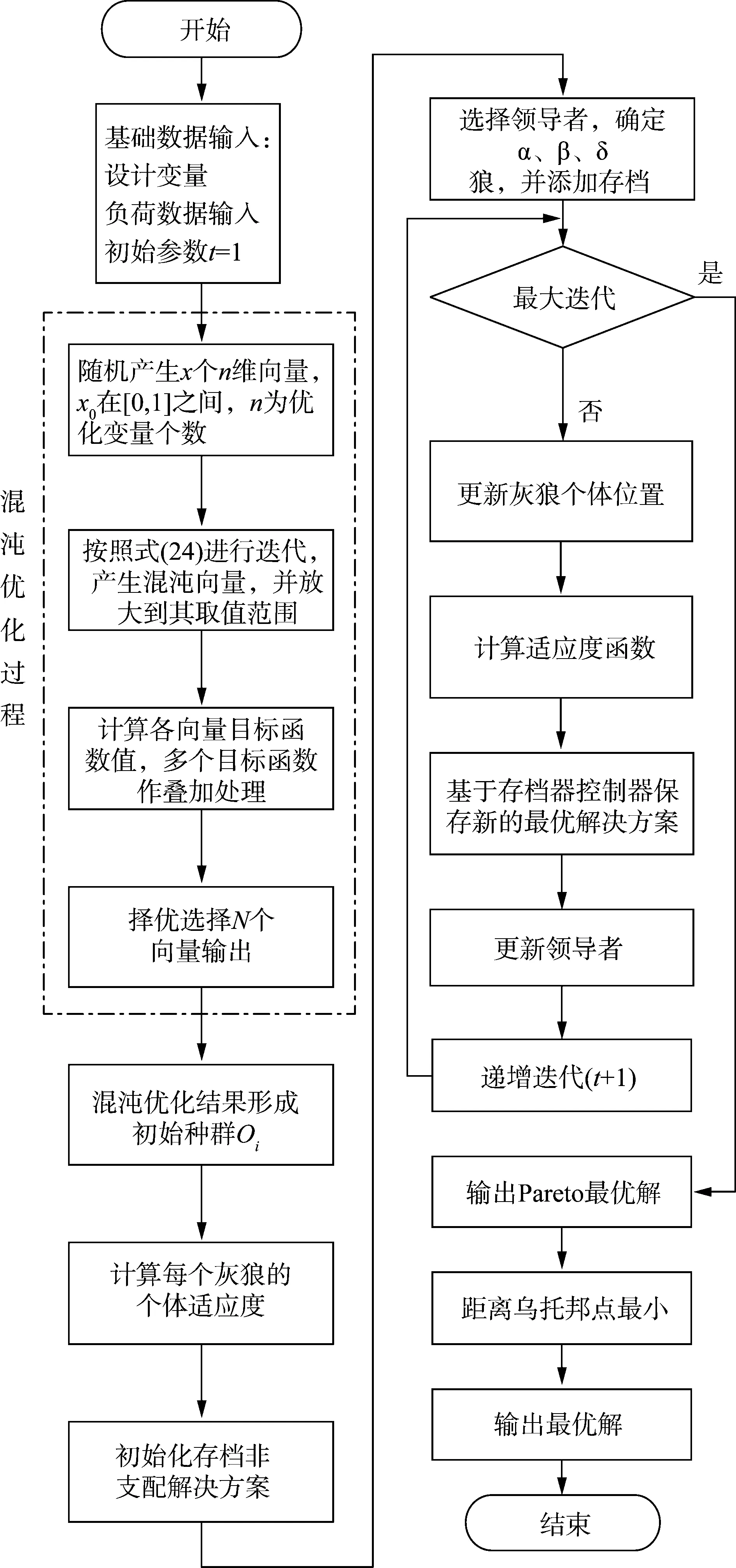
图2 基于Tent映射混沌优化的GWO算法求解流程Fig.2 The solution flow of GWO algorithm based on Tent mapping chaos optimization

3 算例分析

3.1 算例参数

为验证模型的有效性与算法的适用性，本文选取文献[12]冬季与夏季典型日场景对联合系统进行优化调度分析，典型日优化周期T=24 h，优化时间尺度Δt=15 min，系统配备总装机容量为1 000 MW的火电机组、总装机容量为400 MW的风电机组、总装机容量为100 MW的光伏机组和待优化确定的抽水蓄能装机容量。典型日负荷、风电、光伏预测出力如图3所示，风、光、火上网电价与分时电价如图4所示，电价取自文献[23]，火电机组及抽水蓄能机组技术经济参数见表1—2。

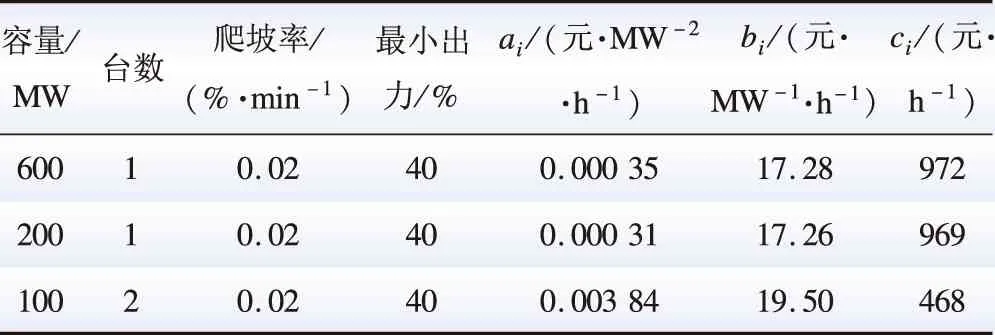
表1 火电机组技术经济参数Table 1 Technical and economic parameters of thermal power units

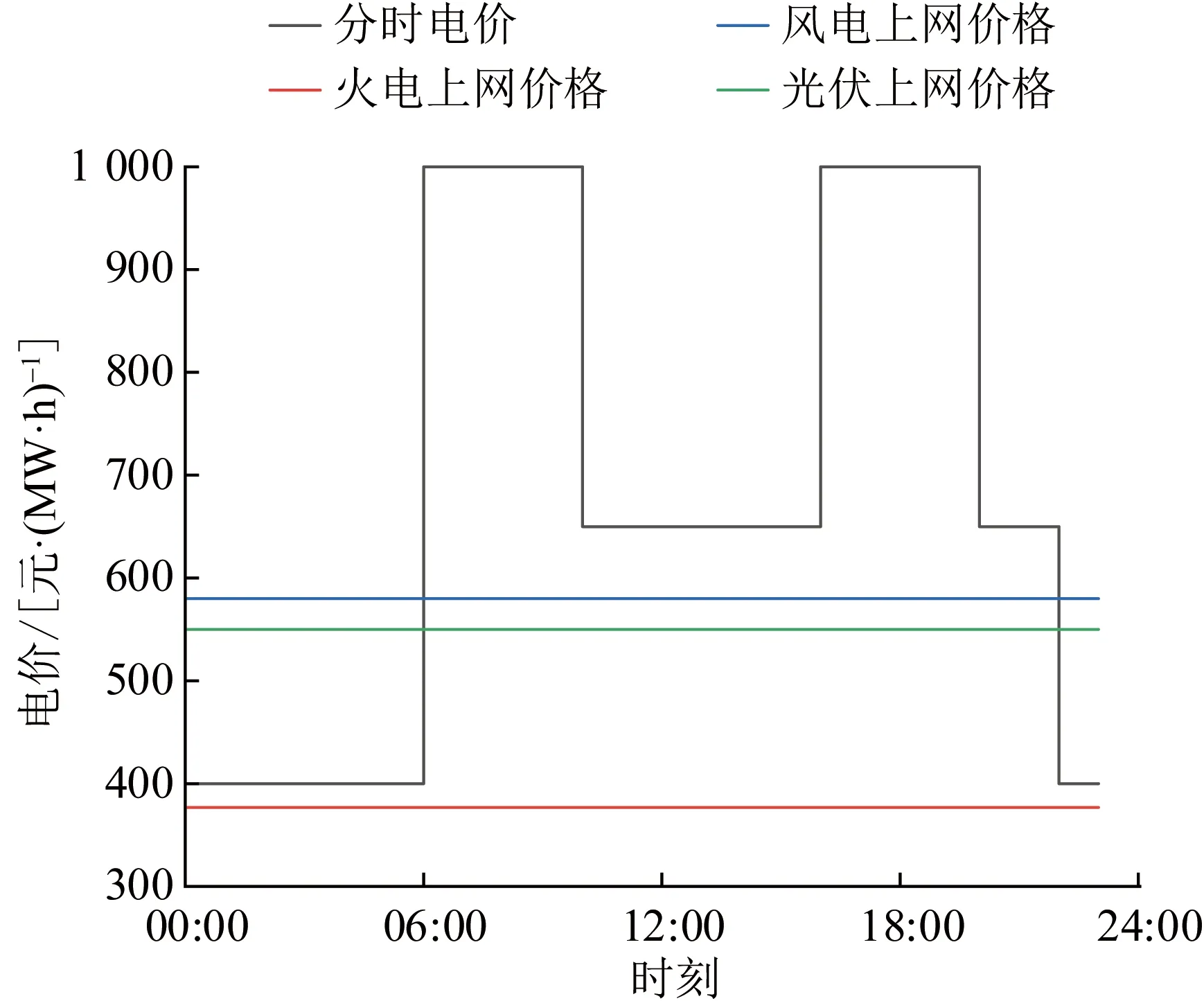
图4 风、光、火上网电价与分时电价Fig.4 Electricity of prices of wind, photovoltaic, thermal power and time-of-use electricity price

由图3可知，夏季日负荷曲线略高于冬季，冬季风资源相较于夏季更丰富，夏季光伏资源相较于冬季更丰富。在负荷低谷时，风资源丰富，且中午出力低于早晚，具有反调峰特性。光伏出力大致与典型日负荷一致，有较强的负荷跟踪能力，具有正调峰特性。

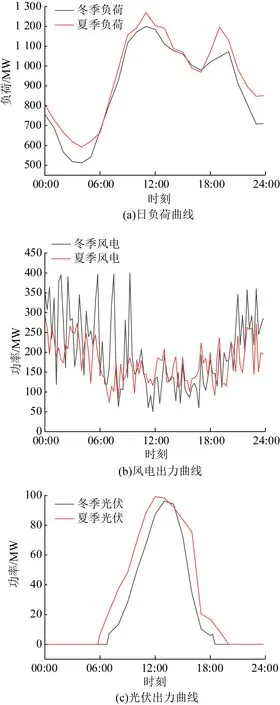
图3 冬季、夏季典型日负荷、风电、光伏出力Fig.3 Typical daily loads, wind power and photovoltaic output in winter and summer

3.2 抽水蓄能电站容量配置结果分析

算例中由于光伏装机容量较小且光伏具有正调峰特性，本文假设光伏优先于风电入网，因此，要获得抽水蓄能的最佳容量配置，即最小化弃风电量。图5为冬季、夏季典型日风电弃风电量。冬季典型日最大弃风功率为277 MW，夏季典型日最大弃风功率为119 MW，当抽水蓄能装机容量280 MW时，可满足最大弃风功率，此时，占风电装机容量的70%。上层模型为下层提供4种容量配置规划方案，分别为占风电装机容量的80%、70%、60%和50%，也即抽水蓄能装机容量分别为320、280、240、200 MW，在这4种情景下对联合系统进行运行调度优化。

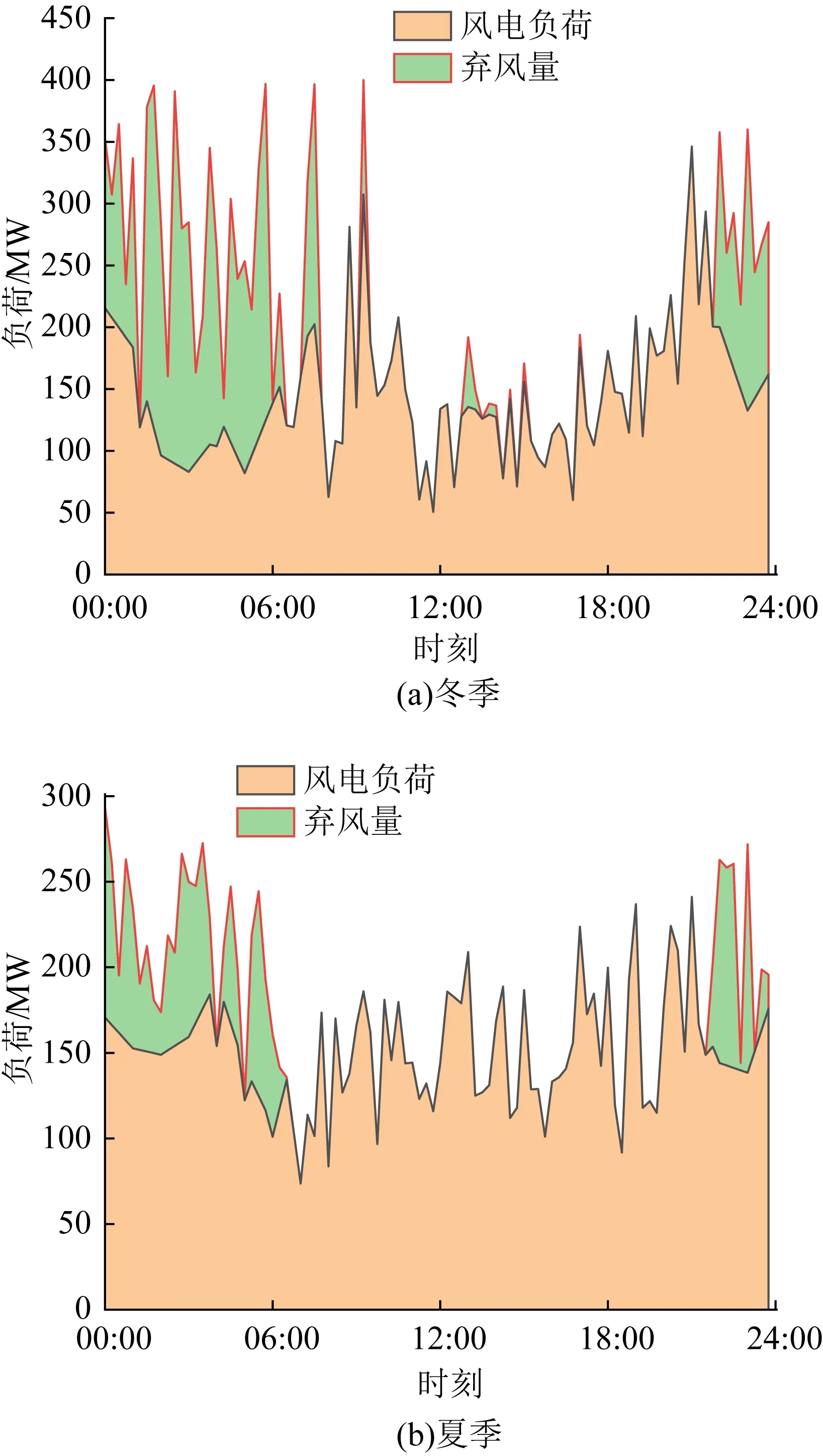
图5 冬季、夏季典型日风电弃风电量Fig.5 Wind power abandoned on a typical day in winter and summer

表2 抽水蓄能机组技术经济参数Table 2 Technical and economic parameters of pumped-storage units

3.3 典型日运行调度优化结果分析

通过基于Tent映射混沌优化的GWO算法，分别对4种含不同容量的抽水蓄能电站在联合系统中的运行调度优化模型进行求解，无抽蓄典型日运行调度结果如图6所示，图7—10分别为装机容量为320、280、240、200 MW的抽水蓄能电站在联合系统中的运行调度优化结果。下层模型求解结果表明，联合系统中加入抽蓄后能够有效减少弃风电量，降低火电机组出力的波动性，减小负荷峰谷差。相比较下，抽水蓄能电站容量为320 MW与280 MW的调节能力更优。

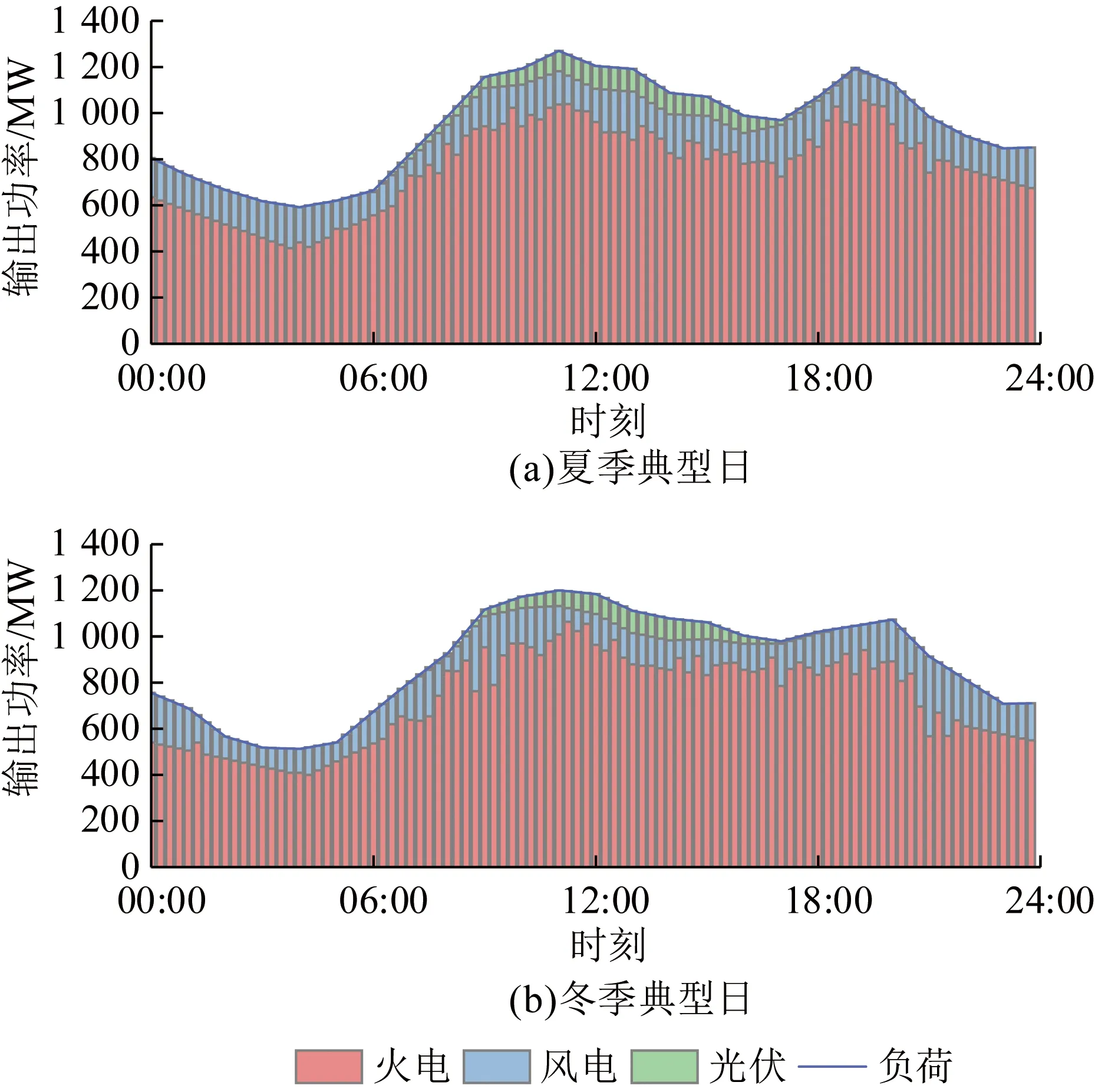
图6 无抽蓄系统典型日运行调度结果Fig.6 Typical daily operation scheduling results without pumping-storage system

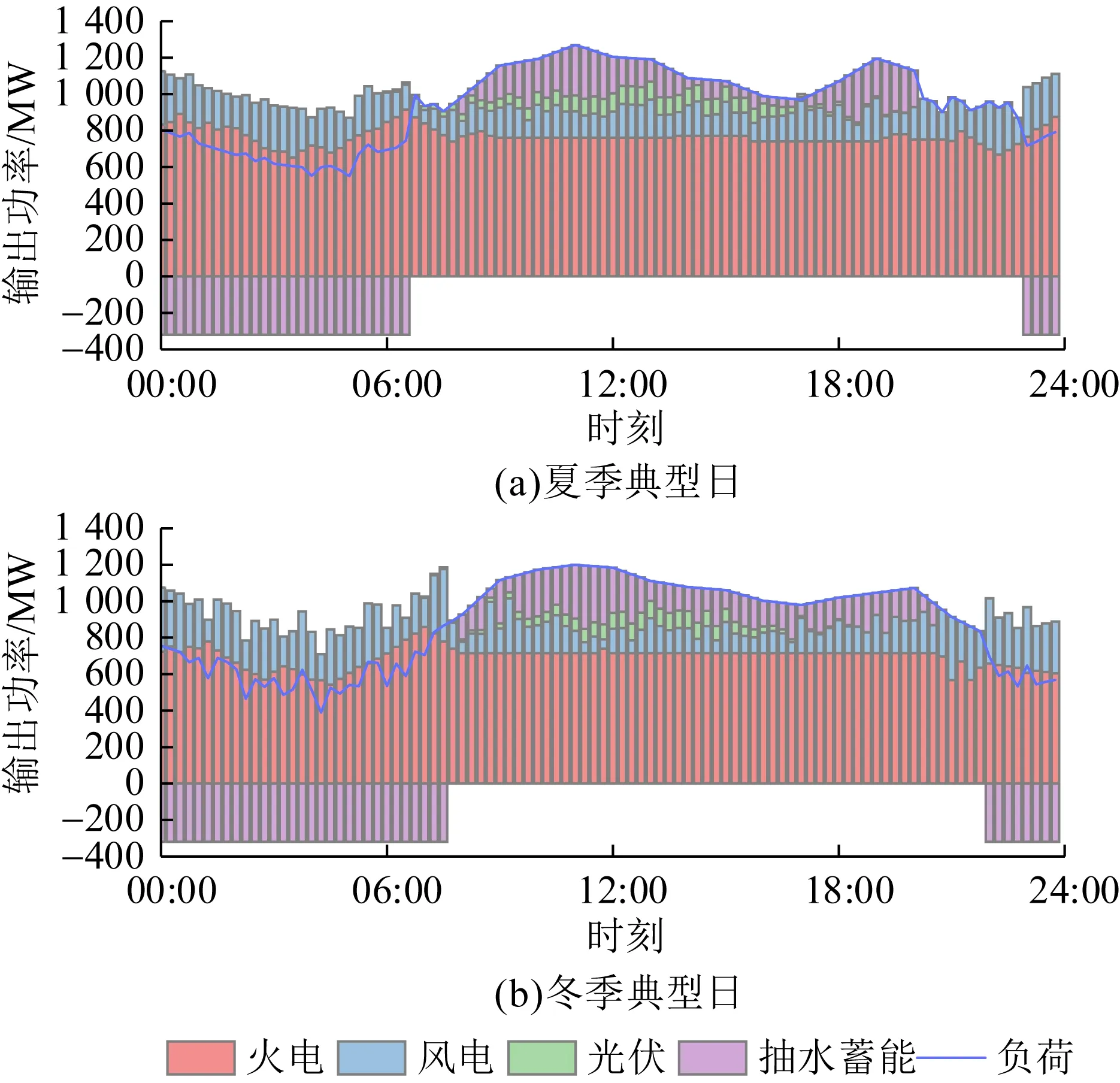
图7 抽水蓄能电站容量为320 MW下联合系统典型日运行调度优化结果Fig.7 Optimal results of typical daily operation scheduling of the combined system with a pumped-storage power station of 320 MW

不同容量配置下典型日系统经济效益结果及抽蓄电站建造成本回收期如表3、表4所示。由表3、4可知，在加入抽水蓄能电站后，联合系统能够获得显著的经济效益，抽蓄容量在满足最大弃风功率后，增加抽蓄容量会提高建造成本，从而降低收益。除联合系统的经济效益外，抽水蓄能电站的成本回收年限也是系统经济性的重要指标。经基于Tent映射混沌优化的改进灰狼算法收敛到最优值，在4种容量配置下，抽水蓄能电站的回收年限都没超过7年，但如果抽蓄无调峰收入，其回收年限会大大增加，说明辅助服务收入是抽水蓄能电站成本疏导的重要途径。4种容量配置下，抽水蓄能电站容量为280 MW时经济效益最佳。

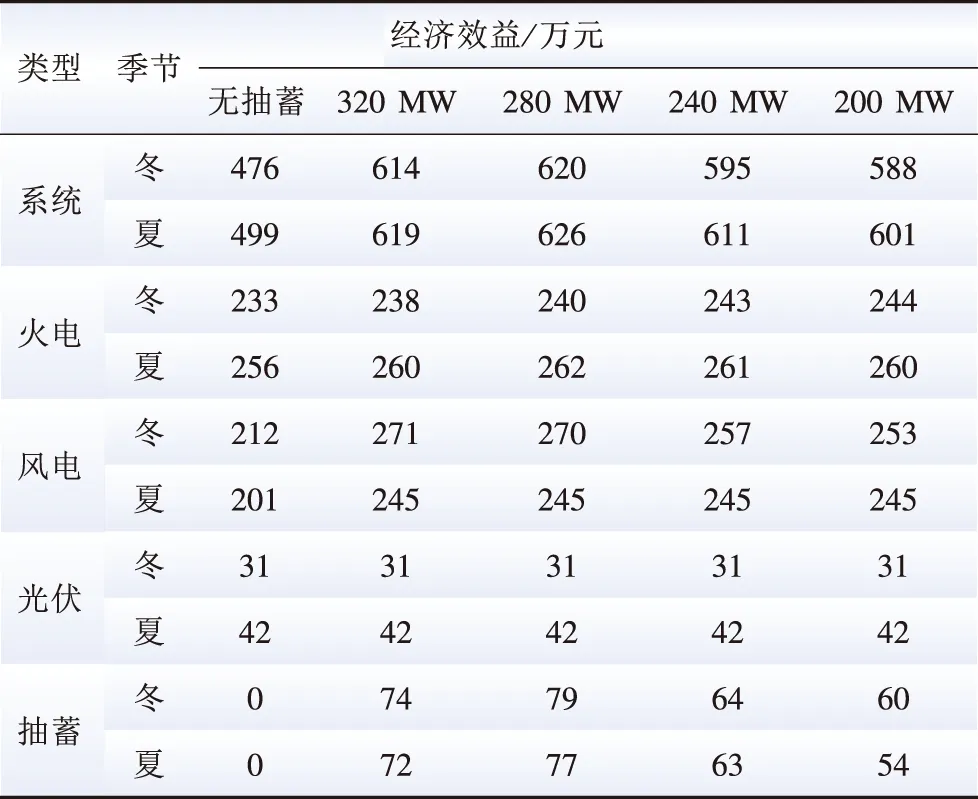
表3 不同容量配置下典型日系统经济效益Table 3 Typical daily system economics with different pumped-storage capacity

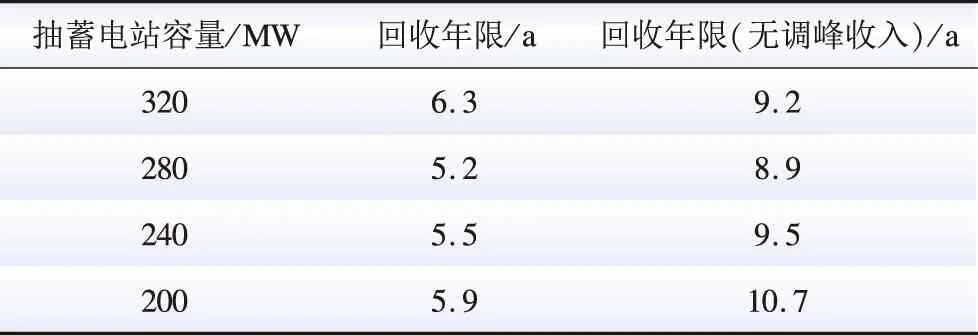
表4 不同容量配置下抽蓄电站建造成本回收期Table 4 Cost recovery period for construction of pumped storage plants with different capacity configurations

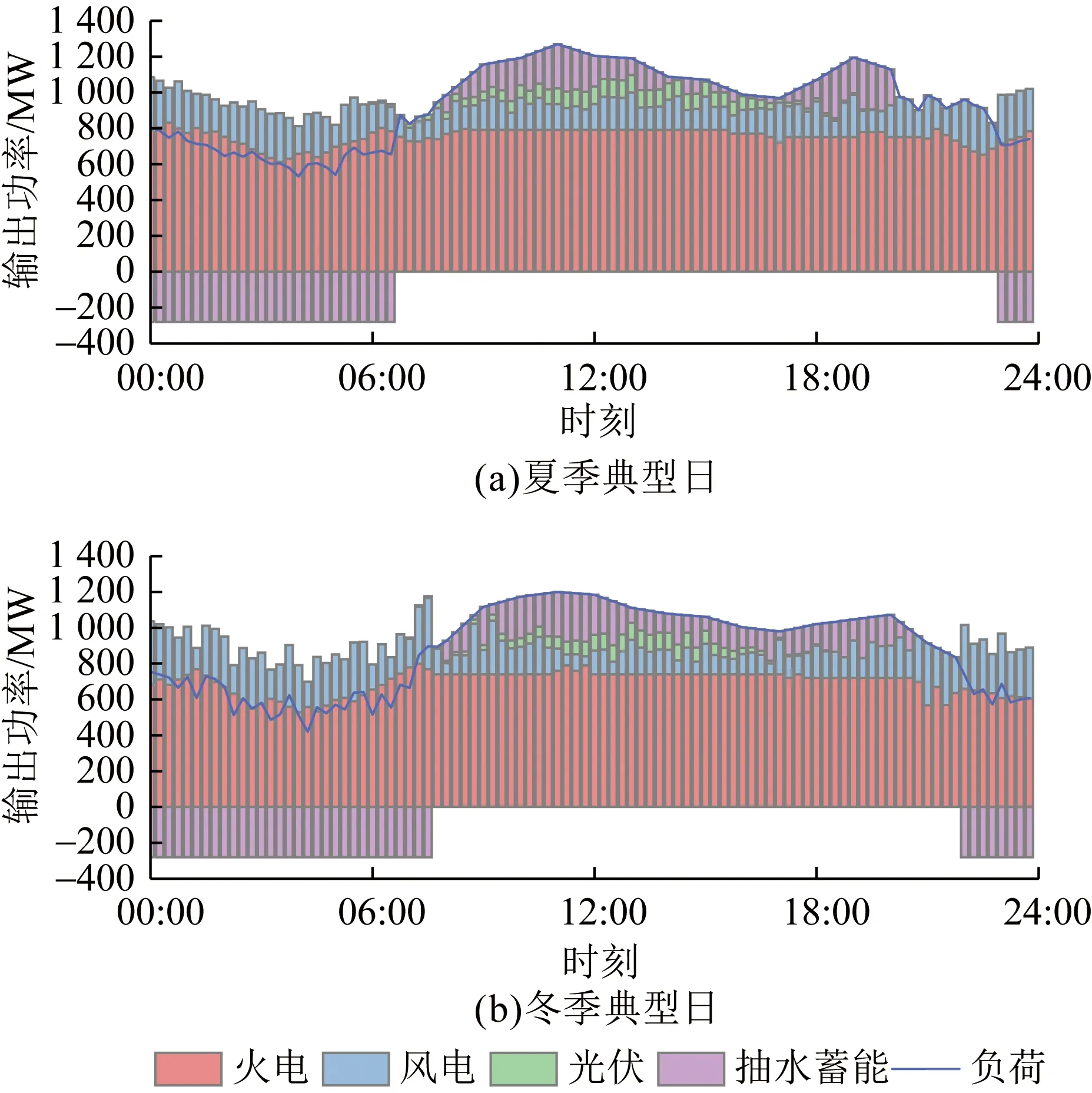
图8 抽水蓄能电站容量为280 MW下联合系统典型日运行调度优化结果Fig.8 Optimal results of typical daily operation scheduling of the combined system with a pumped-storage power station of 280 MW

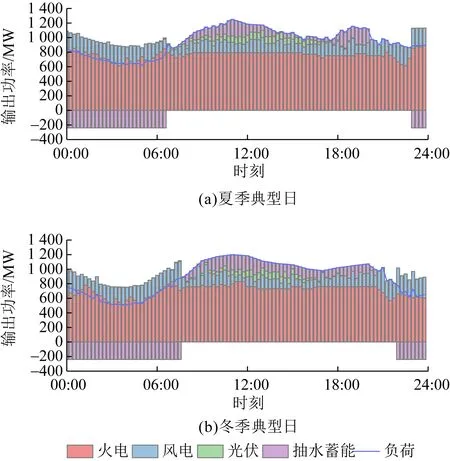
图9 抽水蓄能电站容量为240 MW下联合系统典型日运行调度优化结果Fig.9 Optimal results of typical daily operation scheduling of the combined system with a pumped-storage power station of 240 MW

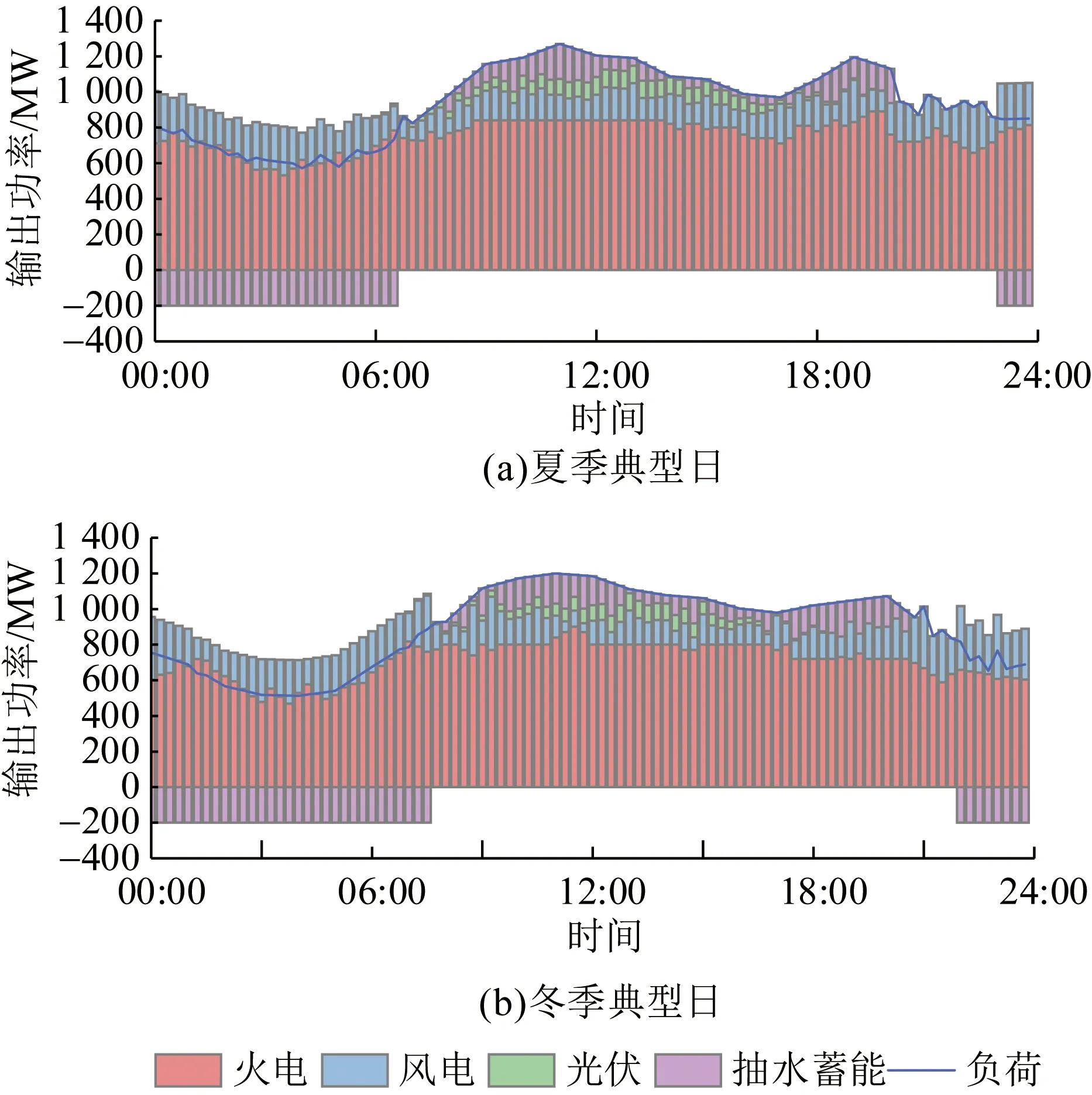
图10 抽水蓄能电站容量为200 MW下联合系统典型日运行调度优化结果Fig.10 Optimal results of typical daily operation scheduling of the combined system with a pumped-storage power station of 200 MW

表5、6分别为不同容量配置下典型日的环境价值与改善系统运行条件结果，结果表明，联合系统加入抽水蓄能电站后，环境价值明显，并能够显著改善系统运行条件，4种容量配置下，抽水蓄能电站容量为320 MW和280 MW时，环境价值与改善系统运行条件结果基本相同，并优于其他容量配置。

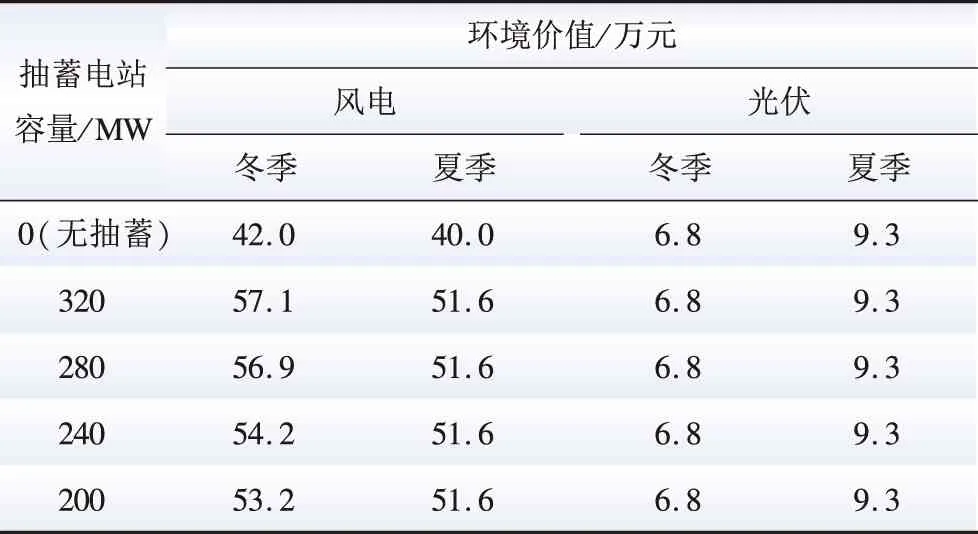
表5 不同容量配置下典型日的环境价值Table 5 Environmental values in a typical day with different pumped-storage capacity

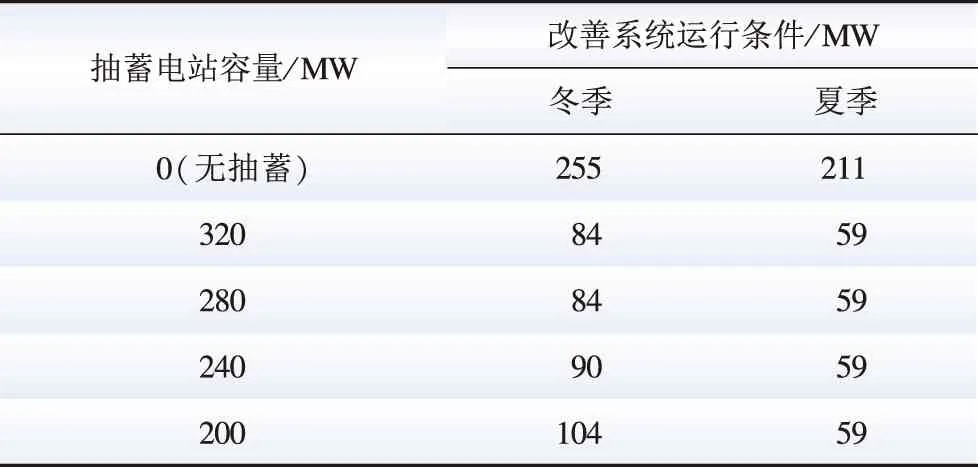
表6 不同容量配置下典型日的改善系统运行条件结果Table 6 Results of a typical day of improved system operating conditions with different pumped-storage capacity

在4种容量配置情景下，抽水蓄能电站容量配置为320 MW和280 MW时，调度运行优化结果明显优于其他容量配置结果，这2种容量配置下环境价值与改善系统运行条件结果基本相同，但280 MW容量配置下经济效益更优。表7为4种容量配置下联合系统的弃风量，通过返回上层检验，抽水蓄能电站容量为280 MW时通过增加较少的弃风量，能够为系统获得较大的经济效益，因此，当联合系统配备容量为280 MW的抽水蓄能电站时，为该特定系统中的最佳容量配置。

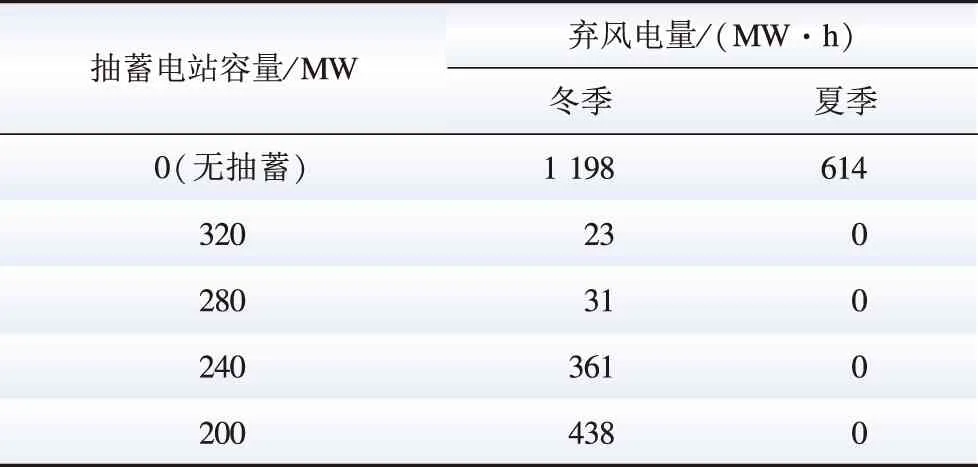
表7 不同容量配置下风电弃风电量Table 7 Wind power abandonment with different pumped-storage capacity

4 结 论

本文综合考虑抽水蓄能电站的容量配置与运行调度优化，构建了联合系统双层规划模型，并提出了求解流程。与其他抽蓄容量配置模型相比，本文站在整个联合系统角度，以弃风、弃光电量之和最小构建上层模型确定容量配置，以计及抽水蓄能电站建造成本的系统售电收入最大，环境价值最大，并同时改善系统运行条件为目标构建下层运行调度优化模型。通过本文研究表明：

1)本文构建的容量配置双层规划模型能够有效减少弃风电量，降低火电机组出力的波动性，减小负荷峰谷差，获得抽水蓄能电站的最佳容量配置，并实现经济效益、环境价值与改善系统运行条件的最大化。

2)辅助服务收入是抽水蓄能电站成本疏导的重要途径。

鉴于本文算例中光伏装机容量较小，且优先光伏入网，下一步研究中将增大光伏装机容量，并且考虑光伏、风电出力的不确定性，进一步完善模型。