基于交替方向乘子法的分布式负荷频率控制策略

李玲芳，陈义宣，许岩，文福拴

(1. 云南电网有限责任公司电网规划建设研究中心，昆明市 650011；2. 浙江大学电气工程学院，杭州市 310027)

0 引 言

负荷频率控制 (load frequency control, LFC) 指根据系统频率变化和联络线传输功率变化调节发电机的有功出力，从而使电力系统频率和联络线交换功率维持在设定的允许范围内[1]。由于很难精确预测负荷需求，需要实时调整发电机有功出力以跟踪负荷需求的动态变化，从而维持系统频率在给定的允许范围之内。导致系统实际频率偏离额定频率。LFC对抑制系统频率偏差和区域间联络线上的功率偏差从而维持电力系统安全稳定运行具有重要意义。

电力系统频率调节包括一次调频和二次调频[2]。在二次调频中，通常采用比例-积分(proportional-integral，PI)控制。不过，PI控制的动态性能高度依赖其增益，而高增益一方面可以提高系统的响应速度，另一方面会恶化系统动态行为从而可能导致系统频率振荡和失稳。在此背景下，本文研究如何设计分布式最优LFC策略来进行二次调频以实现频率偏差为0且系统动态性能最优。

为提升LFC的性能，现有文献中采用了一些先进控制方法设计负荷频率控制器。文献[3-5]采用鲁棒控制策略抑制负荷变化导致的系统频率偏差。文献[6-7]研究了计及通信延迟情况下负荷频率控制器的设计问题。文献[8-9]采用自适应控制策略提升系统运行点发生变化时的系统控制性能。文献[10]采用最优控制策略抑制系统频率偏差和联络线功率偏差。此外，模型预测控制[11]、自抗扰控制[12]、滑模控制[13-14]和事件驱动控制[15]也被用于设计负荷频率控制器以改善控制性能。不过，这些方法应用于实际多区域电力系统负荷频率控制器设计时，参数整定比较困难。基于线性矩阵不等式的鲁棒控制策略的控制器参数整定相对容易，但这种方法通常需要对系统模型进行降阶预处理，从而可能导致系统部分动态特性的丢失。

也有一些文献采用启发式优化算法[16-21]设计负荷频率控制器。文献[22]采用粒子群优化算法整定控制器参数。文献[23]采用灰狼优化算法确定分数阶控制器的参数。不过从理论上无法保证这些启发式优化算法能够获得控制器参数的最优解，尤其是对于实际多区域电力系统，需要优化的控制器参数较多，启发式优化算法就未必能求得最优解。

在上述背景下，本文提出一种基于分布式优化策略的负荷频率控制器设计方法，以优化系统频率控制性能，并提高控制器参数整定的计算效率。在所构建的优化模型中，目标函数包含两项，分别表征控制性能和控制器增益矩阵稀疏度。采用交替方向乘子法(alternating direction method of multiplier, ADMM)求解该优化问题。所提方法具有下述优点：1) 可以获得与集中控制策略相当的频率控制性能，且通讯复杂度较低；2) 利用ADMM的特点可把优化目标分解为可用解析方式求解的2个子优化问题，进而提高参数整定效率，且适用于实际多区域电力系统。最后，以三区域电力系统模型为例对所提方法的可行性和有效性进行验证。

1 负荷频率控制模型

多区域互联电力系统中的每个区域都设有一个调度控制中心，系统频率和区域间联络线上的交换功率均在其监控之中。目前大多数汽轮发电机和水轮发电机都装有调速装置，可以对系统频率变化做出响应。

图1为多区域互联电力系统中第i个区域的负荷频率控制系统框图。尽管电力系统的稳态和动态模型都是非线性的，但负荷频率控制是针对小扰动的，可以近似采用线性化模型[24]。图1中的KBi和KEi为传统的PI控制器参数。

图1所示的第i个区域的模型可用下述微分方程组描述[24]：

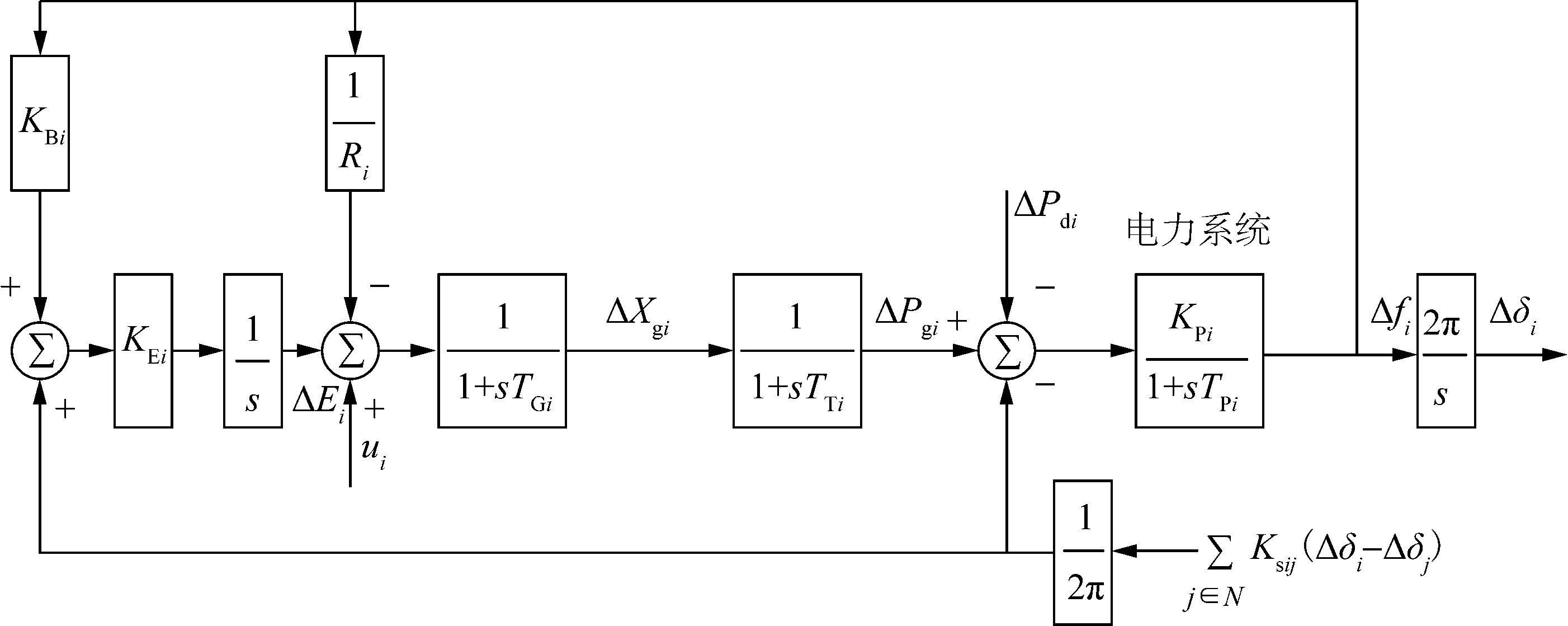
图1 互联电力系统中第i个区域的模型Fig.1 The model of the i-th area in an interconnected power system

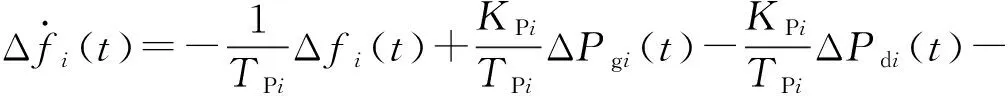
(1)

(2)

(3)

(4)

式中：Δfi(t)、ΔPgi(t)、ΔXgi(t)和Δδi(t)分别表示t

时刻的频率偏差、有功输出调整量、调速器阀门位置调整量和转子角偏差；N表示所研究的互联电力系统中包含的区域数目；ΔPdi(t)表示t时刻的负荷扰动；TGi、TTi和TPi分别表示调速器、汽轮机和电力系统的时间常数；KPi和Ri分别表示电力系统的增益和速度调节系数；Ksij表示区域i和区域j之间的连接增益，如果这2个区域间没有功率交换则Ksij为0；ui(t)表示区域i的辅助控制输入。

为便于表述，可将微分方程组式(1)—(4)改写成矩阵形式：

(5)

式中：Xi(t)和Xj(t)分别表示区域i和区域j在t时刻的状态向量，Xi(t)=[Δfi(t) ΔPgi(t) ΔXgi(t) Δδi(t)]T；Ui(t)表示控制器在t时刻的输入向量；

2 分布式最优负荷频率控制器设计

根据式(5)，包含n个区域的互联电力系统的负荷频率控制问题可描述为：

(6)

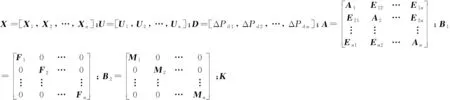
在互联电力系统中，一个区域内的负荷扰动可能会对另一个区域造成明显影响，严重时甚至会产生级联故障(cascade failure)。为尽可能降低这种区域间的耦合影响，可以采用最优控制策略实现负荷频率控制[10]。虽然采用集中最优控制策略设计控制器增益K可以实现良好的负荷频率控制性能，但其对区域间的信息实时交互要求较高。另一方面，描述多区域互联电力系统动态过程的微分方程组相当复杂，这对采用集中优化策略实现负荷频率控制带来了很大困难。

本文所研究的负荷频率控制器设计方法可以用下述优化问题描述：

minJ(K)+γg(K)

(7)

s.t.(A-B2K)TP+P(A-B2K)=
-(Q-KTRK)

(8)

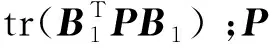
式(8)所描述的等式约束为系统稳定条件，可通过动态系统稳定性理论分析得到[26]。

式(7)中的优化目标包含两项：J和g。J表示传统的控制性能指标。仅以指标J作为优化目标时，可实现对频率控制性能的优化。但这种集中控制策略需要反馈的信号数量较多，因此增加了区域间信息实时交互的复杂度。g为控制器增益矩阵稀疏度指标，g的值越小，控制器增益矩阵的非零元素越少，需要反馈的信号数量也就越少。本文采用J和g之和作为优化目标，以兼顾最优控制性能和降低区域间信息交互的复杂程度这两方面的期望。

由于式(7)中的优化目标同时包含了指标J和指标g，在求解由式(7)和(8)所描述的优化模型时，采用传统基于梯度的求解方法一般只能求得局部最优解。采用ADMM算法可以有效求解这个问题。ADMM算法将要求解的优化问题分解为2个子优化问题，然后对这2个子优化问题交替迭代求解，最终求得原始优化问题的解。理论上已证明采用ADMM算法可求得控制器参数的最优解[27]。

采用ADMM算法求解式(7)和(8)所描述的优化模型的步骤如下：

步骤1：将式(7)和(8)所描述优化模型分解为2个子优化问题。

采用g(G)表示式(7)中指标g(K)，则由式(7)和(8)所描述的优化模型可分解为2个子问题：针对K优化系统的频率偏差指标J(·)

(9)

和针对G优化控制器结构指标g(·)

(10)

Lp(K,G,Λ)=J(K)+γg(G)+

tr[ΛT(K-G)]+ (ρ/2)‖K-G‖2

(11)

式中：Λ表示拉格朗日乘子；ρ表示正的标量。

步骤2：交替求解子优化问题式(9)和式(10)。

基于ADMM的方法架构，通过对子优化问题式(9)和式(10)交替求解，最终可求得分布式最优负荷频率控制策略；这种方法的计算效率较高，适用于决策变量较多的优化问题。采用ADMM算法求解这2个子优化问题的过程如图2所示，其具体实现流程可参看文献[27]，因篇幅所限这里不再赘述。

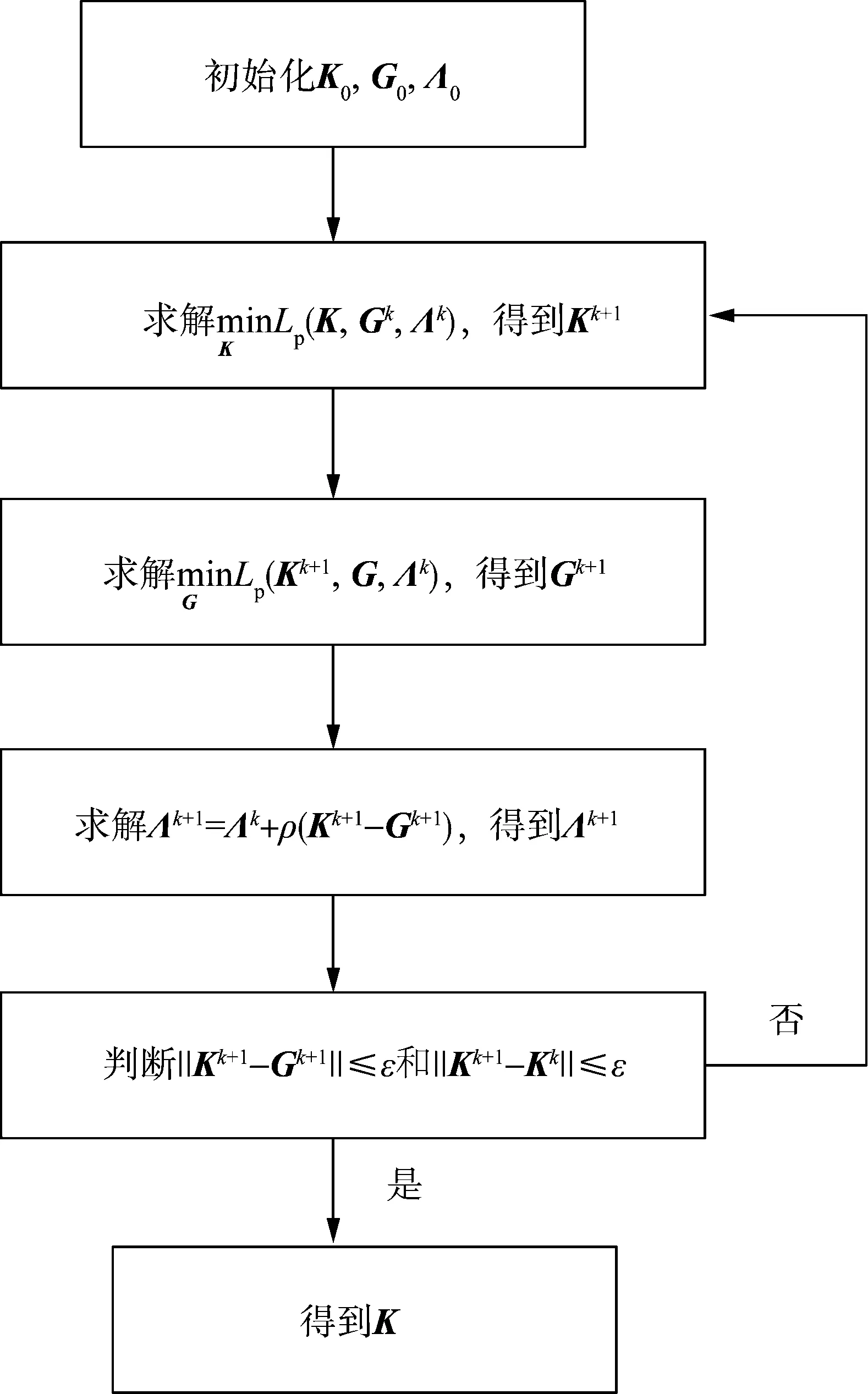
图2 基于ADMM的分布式最优负荷频率控制器设计过程Fig.2 Design procedure of the ADMM-based distributed optimal load frequency controller

3 算例与结果

3.1 算例参数

采用一个三区域电力系统算例来说明所提分布式负荷频率控制策略的有效性。IEEE 10机39节点电力系统即新英格兰测试系统[28]可划分为3个区域，连接母线3和4、14和15、16和17为3个区域之间的联络线。根据文献[29]，经过抽象建模之后的三区域控制系统连接框图如图3所示。u1、u2和u3为输入的控制信号，由所提出的控制策略优化确定。区域1和区域3采用图1所示的汽轮机调速系统模型。区域2采用水轮机调速器系统，其数学模型如下详述[28]。

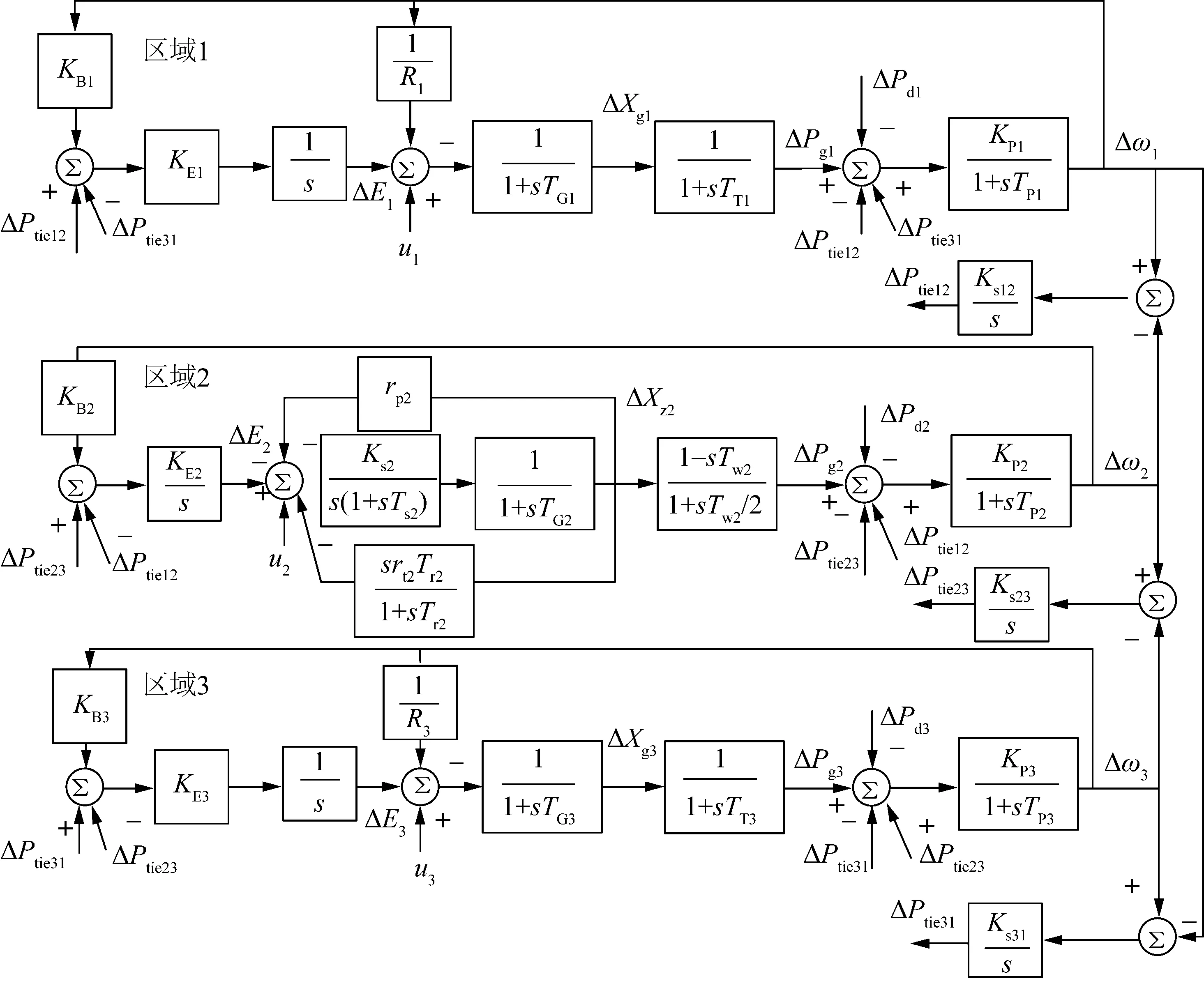
图3 三区域电力系统模型框图Fig.3 Block diagram of a three-area power system model

(12)

(13)

(14)

(15)

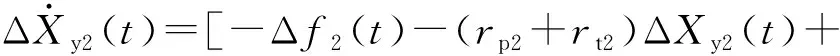
(16)

(17)

式中：ΔPg2(t)表示水轮机有功输出调整量；ΔXz2(t)表示阀门位置调整量；ΔXm2(t)表示引导阀位置调整量；ΔXy2(t)表示阀门动作速度补偿调整量；Tw2表示水流惯性时间常数；TG2表示调速器时间常数；Tr2表示软反馈时间常数；rt2表示软反馈增益；rp2表示下垂系数；Ks2为增益。

本文在MATLAB2016b编程环境下进行仿真研究。参数设置为：KP1=120 Hz/pu,KP2=112.5 Hz/pu,KP3=115 Hz/pu;TP1=20 s,TP2=25 s,TP3=20 s；TG1=0.08 s，TG2=0.20 s，TG3=0.07 s；TT1=0.3 s，Tw2=1 s，TT3=0.35 s；R1=2.4 Hz/pu,rp2=0.04 pu,R3=2.5 Hz/pu；Tr2=6 s；rt2=0.5 pu;Ks2=0.2 pu；Ks12=Ks13=Ks21=Ks23=Ks31=Ks32=0.5 pu/Hz。

3.2 控制器增益矩阵

通过图2所示算法，可得到控制器增益矩阵K，其结构如图4所示。在图4中，蓝色的点表示该处矩阵元素不为0。从图4中可以看出，当γ=0.000 10时，K的所有元素都不为0，即控制结构为集中模式；这意味着对每个区域的控制器设计而言都需要用其相邻区域的系统状态信息来计算式(6)中的控制信号U。随着γ值的增加，K中的零元素越来越多；当γ=0.390 690时，K中只有9个非零元素，此时控制器结构呈现分布式特征，且区域间需要交互的系统状态信息最少。

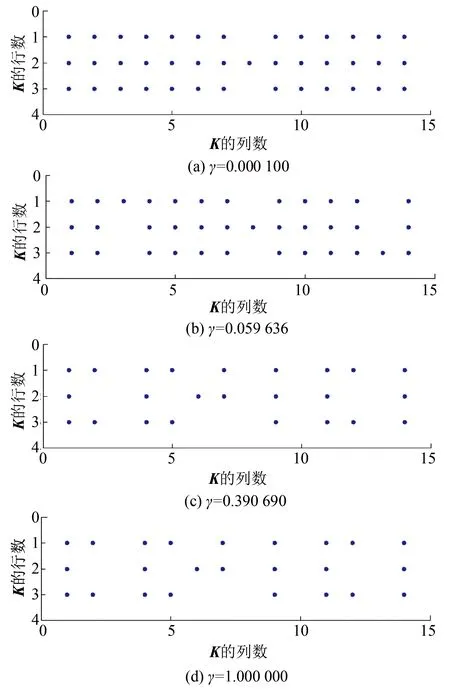
图4 控制器增益矩阵K的结构Fig.4 Structure of the gain matrix K

3.3 控制性能及与现有方法比较

本节通过算例对所提分布式负荷频率控制策略和传统基于PI的负荷频率控制策略进行对比分析，以说明所提方法的有效性。给定3个区域所受到的负荷扰动分别为ΔPd1=0.010 pu、ΔPd2=0.020 pu和ΔPd3=0.015 pu。

当采用基于PI的负荷频率控制策略时，获得的系统频率响应偏差和区域间联络线功率响应偏差如图5所示。可以看出，这2个偏差在15 s时均仍存在微小振荡。

采用集中式负荷频率控制策略时，控制器增益矩阵结构如图4(a)所示。系统的频率响应偏差和联络线功率响应偏差如图6所示。从图中可以看出，3个区域的频率偏差在15 s时几乎为0。与图5对比可知，采用集中式负荷频率控制策略时的频率响应超调量更小。比较图5和图6中的功率响应曲线可得类似结论。因此，采用集中式负荷频率控制能有效抑制负荷扰动造成的系统频率偏差和联络线功率偏差，并改善频率控制性能。

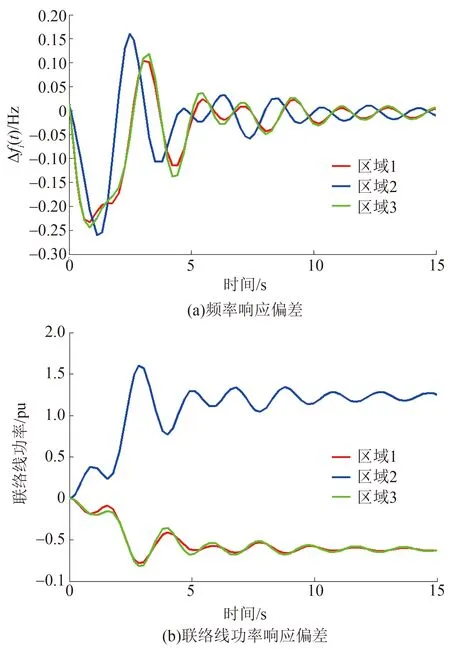
图5 基于PI的负荷频率控制响应曲线Fig.5 Response curves of the three-area interconnected power system with the PI-based LFC strategy under load disturbances

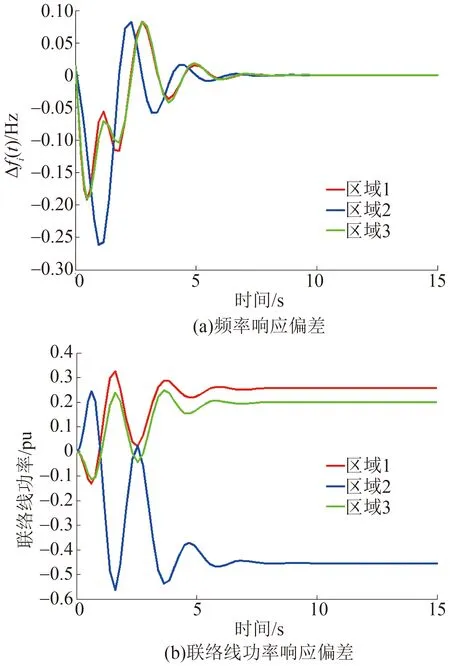
图6 集中式负荷频率控制响应曲线Fig.6 Response curves of the three-area interconnected power system with the centralized LFC strategy under load disturbances

采用所提分布式负荷频率控制策略时，控制器增益矩阵结构如图4(d)所示。系统的频率响应偏差和联络线功率响应偏差如图7所示。可以看出3个区域的频率偏差在15 s时几乎为0。与图6对比可知，采用所提分布式负荷频率控制策略时的频率控制性能与集中式负荷频率控制一致，只是区域1和区域3的频率偏差响应的超调量在2.5 s附近存在微小差异。比较图7和图6中的功率响应曲线可得类似结论。因此，由3.2节的分析可知，采用图4(d)所示控制器结构的信息交换复杂程度低于采用图4(a)所示控制器结构。因此，所提分布式负荷频率控制策略具有较低的通信复杂度。

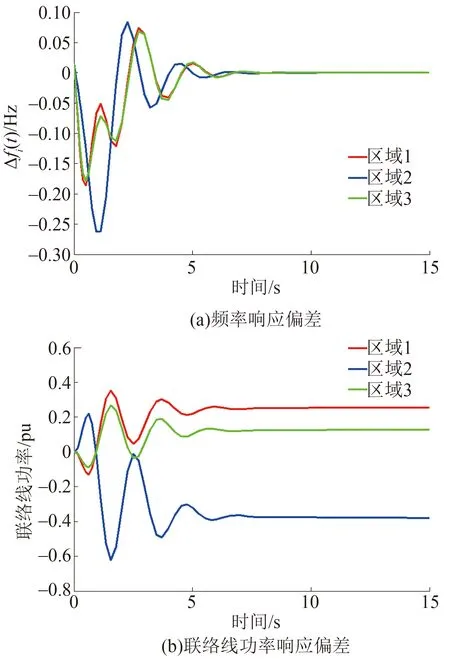
图7 分布式负荷频率控制响应曲线Fig.7 Response curves of the three-area interconnected power system with the distributed LFC strategy under load disturbances

4 结 语

本文提出基于交替方向乘子法的分布式负荷频率控制策略，以优化频率控制性能，且降低对区域间信息的交互需要从而提高计算效率。在所提优化方法中，目标函数包含二次最优控制性能指标和控制器增益矩阵稀疏化指标；该优化问题被转化为2个子优化问题并采用ADMM有效求取控制器增益矩阵，从而降低了控制器实现的复杂程度。采用含三区域的互联电力系统进行仿真验证，计算结果表明针对负荷扰动和时变参数，所提方法能把系统频率偏差和区域联络线功率偏差控制到0。

后续研究工作将针对区域间实时交换的信息数据不完整或有错误时，对所提方法进行测试并基于相关结果对所提分布式负荷频率控制设计方法进行改进和发展。