一种新的电-气互联多区域综合能源系统最优能流计算方法

郑重, 苗世洪,赵海彭,尹斌鑫

(1.强电磁工程与新技术国家重点实验室(华中科技大学)，武汉市 430074；2.电力安全与高效湖北省重点实验室(华中科技大学)，武汉市 430074)

0 引 言

21世纪以来，面对资源制约日益加剧、生态环境约束凸显等问题，我国坚持节约资源和保护环境的基本国策，积极转变经济发展方式，并相继出台了《能源发展战略行动计划》、《能源生产和消费革命战略》等纲领性文件及《能源技术革命创新行动计划》等专项文件[1-3]。随着我国经济社会持续发展，能源生产和消费模式正在发生重大转变。在此背景下，研究综合能源系统协调优化运行策略，是充分挖掘能源利用潜力，构建清洁低碳、安全高效的现代能源体系的重要前提。

目前，国内外针对综合能源系统最优能流问题已展开了大量研究。文献[4]提出了一种电-气混联系统双层多时间尺度优化调度算法。文献[5]同时考虑分时电价及“冷热电气”综合需求响应的影响，建立了以商业园区总运行成本最小为优化目标的综合能源系统优化运行模型。文献[6]利用动态场景方法刻画新能源出力的不确定性，并以此为基础建立了考虑新能源出力不确定性的电气综合能源系统协同优化模型。针对综合能源系统经济优化调度中天然气模型精度不足的问题，文献[7]提出了一种考虑天然气流动特性的电-气综合能源系统经济优化调度模型。文献[8]以提升综合能源系统灵活安全性为目标，提出了考虑多能灵活性的综合能源系统多时间尺度优化调度策略。上述文献多采用集中式算法求解综合能源系统最优能流问题，与此同时，部分文献采用分布式算法将综合能源系统最优能流问题分解为若干子问题，并通过迭代使模型收敛至最优解。文献[9-10]采用交替方向乘子法(alternating direction method of multipliers，ADMM) 实现模型分布式求解，在保证系统间信息交互的同时提升数据保密性。文献[11]构建针对区域综合能源系统的日前-日内两级优化调度模型，并利用基于Levy变异的改进烟花-混合蛙跳算法进行求解。上述研究主要针对单个综合能源系统优化问题展开研究，随着综合能源系统规模的进一步扩大，系统间信息数据交互将进一步增强，进而对算法求解速度、收敛性等带来严峻挑战。

近年来，多个综合能源区域系统的跨区互联已成为现代能源互联网的典型特征，区域互联的主要优势在于可通过资源整合实现资源共享和风险分担[12]。在综合能源系统分区优化调度层面，文献[13]面向具有多个平级主体的多区互联电-气综合能源系统环境，提出了一种基于嵌套交替方向乘子法的综合能源系统分区优化模型求解算法。文献[14]构建了以能量枢纽为基本决策主体的电-气能量流解耦机制，并进而提出基于能量枢纽的综合能源系统多主体协同优化调度模型。文献[15]针对考虑热网交互的综合能源系统规划和运行优化技术开展研究，并建立多区域综合能源系统多目标优化模型。

上述文献针对综合能源系统内多能流耦合关系开展了大量研究，并以此为基础建立计及系统经济性、可靠性、灵活性的综合能源系统多目标最优能流模型。但现有研究多采用集中式优化求解框架，随着综合能源系统规模的不断扩大，集中式优化方法存在数据维度高，约束冗杂，求解复杂，收敛困难等诸多问题，对于调度中心的计算能力和通信能力亦提出了严峻挑战。与此同时，传统分布式求解算法在针对多个综合能源系统主体时收敛性亦无法得到保证。此外，上述研究在建立电网及气网模型均存在一定简化及近似，因此模型求解精度必将受到一定影响。

针对上述问题，本文构建了一种基于二阶锥松弛(second order cone relaxation, SOCR)和自适应步长ADMM的电-气互联多区域综合能源系统最优能流计算方法。首先，针对单个电-气互联综合能源系统最优能流问题，提出一种基于SOCR的电-气综合能源系统集中式优化模型。然后，在此基础上，本文进一步考虑多综合能源系统区域间能量信息交互，提出一种基于自适应步长ADMM的多区域综合能源系统最优能流求解方法。算例结果表明，本文所提出的多区域综合能源系统最优能流计算方法能够充分计及综合能源系统间能量信息交互，在确保计算精度的前提下显著提升模型收敛性。

1 电-气互联综合能源系统模型

本文以电-气互联综合能源系统为研究对象，首先建立综合能源系统各子系统优化模型，主要包括配电网模型、燃气网络模型及燃气轮机(micro-turbine，MT)模型。

1.1 配电网模型

1.1.1 目标函数

配电网模型优化目标为配电网总运行经济成本最小，包括配电网购电成本和弃风成本，具体表达式如下：

minfdis=Ccost+Cpub

(1)

(2)

(3)

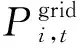
1.1.2 约束条件

配电网约束条件主要包括功率平衡约束、节点电压约束、分布式发电出力约束及线路载流量约束等，具体表达式如下。

1)功率平衡约束。

功率平衡约束为电力系统最基本的约束，配电网运行时必须考虑系统有功及无功平衡约束：

(4)

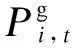
2)潮流约束。

配电网交流潮流约束可表示为：

(5)

式中：Gij,Bij分别表示支路i-j的电导和电纳值；Ui,t,Uj,t分别表示t时刻节点i和节点j的电压大小；θij,t表示t时刻i节点与j节点之间的电压相位差。

3)风电出力约束。

风电最大可接入有功功率可表示为：

(6)

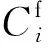
4)节点电压约束。

配电网中各节点均应满足节点电压约束，即：

Umin≤Ui,t≤Umax

(7)

式中：Ui,t表示第i个节点t时段内节点电压大小；Umax和Umin分别表示节点电压上下限。

5)配电网购电量约束。

由于配电网中通常不存在火电机组，因此，为满足电力电量平衡，配电网需要向上级主网购电，配电网购电量约束可表示为：

(8)

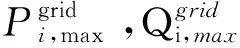
6)线路载流量约束。

配电网线路载流量约束可表示为：

0≤Iij≤Iij,max

(9)

式中：Iij表示支路i-j的载流量大小；Iij,max表示支路i-j的载流量上限。

1.2 气网模型

1.2.1 目标函数

气网模型优化目标为系统总经济成本最小，主要考虑系统购气费用，具体表达式如下：

(10)

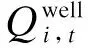
1.2.2 约束条件

气网约束条件主要包括管道气压气流约束、节点气流平衡约束及气源流量约束等，具体表达式如下：

1)管道气压气流约束。

天然气管道气压气流约束可用Weymouth方程表示为：

(11)

式中：qij,t表示t时刻管道i-j的稳态流量；Sij表示管道i-j气流方向标志位；Cij表示管道i-j等效气阻抗参数；πi,t表示i节点t时刻气压大小。

(12)

2)节点气流平衡约束。

天然气网络各节点应满足气流平衡约束，即天然气网络节点气流可用支路气流表示为：

(13)

式中：qi,t表示i节点t时刻气流量大小；Λ(i)表示向i节点注入气流的节点集合；Γ(i)表示i节点流出气流节点集合。

3)气源流量约束。

气井产气量应满足约束：

(14)

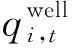
4)节点气压约束。

为确保天然气网络安全稳定运行，天然气网络节点气压需满足约束：

πi,t,min≤πi,t≤πi,t,max

(15)

式中：πi,t表示节点i在t时刻气压大小，πi,t,max、πi,t,min分别表示节点i气压上下限。

5)管道流量约束。

与电力网络类似，天然气网络亦需要满足管道流量约束：

qij,t,min≤qij,t≤qij,t,max

(16)

式中：qij,t,max,qij,t,min分别表示管道i-j气流量上下限。

1.3 燃气轮机模型

1.3.1 目标函数

燃气轮机模型是综合能源系统内电网络与气网络的重要耦合枢纽，能够有效实现气-电转换，因此燃气轮机模型优化目标为购气成本最低，即：

(17)

式中：fMT为燃气轮机模型总运行经济成本；Ωmt表示燃气轮机模型集合；Qmt,i,t表示i节点t时刻燃气轮机模型耗气量。

1.3.2 约束条件

燃气轮机模型应当满足气-电转换约束，燃气轮机模型气-电转换关系可表示为：

(18)

式中：Pmt,i,t为i节点t时刻MT输出有功功率；α、β、γ为MT转换二次项、一次项及常系数。

2 多区域电-气互联综合能源系统最优能流计算方法

2.1 基于SOCR的电-气互联综合能源系统最优能流凸优化模型

由前述分析可知，本文所建立的电-气互联综合能源系统优化模型中，由于电网交流潮流约束中包含乘积项及三角函数项，气网管道气压气流约束亦包含乘积项，因此二者构成的可行域集合不为凸集，原始电网及气网模型中均存在非凸项，从而导致模型无法使用成熟商业软件进行求解。近年来有部分学者采用启发式算法[11]对该问题进行求解，但求解精度及收敛性均无法得到保证。因此，本文进一步引入SOCR方法，对原始模型非凸约束进行转换，具体流程如下。

SOCR转换首先需要进行变量定义。针对电网非凸约束，定义：

(19)

根据定义可知，Ji,t、Kij,t、Hij,t满足约束：

Kij,t-Kji,t=0

(20)

Hij,t+Hji,t=0

(21)

(22)

由于式(22)仍然为等式非凸约束，因此进一步将式(22)松弛为：

(23)

式(23)可进一步写为二阶锥标准形式：

(24)

利用式(19)所定义变量进行替换，式(5)、(7)、(9)进而转换为：

(25)

(26)

Ji,min≤Ji,t≤Ji,max

(27)

类似地，对于气网Weymouth方程，首先需要对气流方向标志位进行替换，引入0-1变量z，该变量满足约束：

(28)

利用该变量，进一步将式(12)、(16)分别转换为：

(29)

qij,t,min(1-z)≤qij,t≤qij,t,maxz

(30)

针对式(29)左侧乘积项所引入的模型非凸约束，进一步定义变量：

Zi=zγi,Zj=zγj

(31)

则有：

(32)

根据式(31)所定义的变量，式(29)转换为：

(33)

类似地，将式(33)所示的等式非凸约束松弛为：

(34)

进一步将式(34)写成矩阵形式的二阶锥标准形式：

‖qij‖2≤cx

(35)

(36)

(37)

至此，原始非凸电-气互联综合能源系统最优能流模型的二阶锥近似已经完成，进而确保了模型求解过程可在多项式时间内完成[16]。

2.2 基于自适应步长ADMM算法的多区域综合能源系统最优能流分布式计算

2.1节提出了一种单区域综合能源系统集中式优化求解思路。随着多个综合能源系统跨区域互联现象的日益增多，针对多区域综合能源系统协同最优能流问题，进一步引入自适应步长ADMM算法进行分布式求解。

首先，构造多区域综合能源系统最优能流模型增广拉格朗日函数。以两区域综合能源系统最优能流模型为例，系统增广拉格朗日函数LIES可表示为：

(38)

式中：LIES表示系统增广拉格朗日函数；FIES,i表示第i个综合能源系统总经济成本；NIES表示综合能源系统数量；λ1、λ2分别为综合能源系统1、2对应拉格朗日乘子；ρ为综合能源系统1、2惩罚系数；Pmt1,t、Pmt2,t分别表示综合能源系统1、2在t时刻交互电功率大小。两区域综合能源系统最优能流问题可进一步分解为2个子优化问题：

(39)

(40)

系统拉格朗日乘子迭代公式可表达为：

(41)

对于自适应步长ADMM算法，系统惩罚系数迭代公式可表达为：

(42)

式中：rk、sk分别表示第k次迭代系统原始残差和对偶残差，其计算公式如下：

(43)

(44)

(45)

进而ADMM算法收敛判据可表示为：

(46)

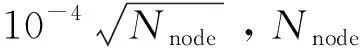
由式(42)可知，相较于传统定步长ADMM算法，自适应步长ADMM算法能够平衡原始残差与对偶残差收敛速度，降低系统振荡。同时，由于本文所构建基于SOCR的电-气互联综合能源系统最优能流问题属于凸优化问题，自适应步长ADMM算法可确保模型收敛至最优解[4]。

2.3 基于SOCR和自适应步长ADMM的多区域综合能源系统最优能流计算

在上述研究的基础上，本文进一步构建基于SOCR和自适应步长ADMM算法的多区域综合能源系统最优能流计算方法。该方法采用集中-分布式求解框架，对于单个综合能源系统，利用SOCR实现模型非凸约束转换，进而采用集中式算法进行求解；对于多个综合能源系统，利用自适应步长ADMM进行分布式求解，最终获取多区域综合能源系统最优能流求解结果，具体流程如下：

1)基本数据输入，确定综合能源系统网络拓扑、电气负荷大小，购能成本等基本参数。

2)建立基于SOCR的电-气互联综合能源系统最优能流模型。

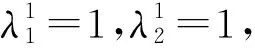
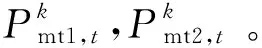
5)分别根据式(41)—(42)，依次更新系统拉格朗日乘子及惩罚系数。

6)分别根据式(43)—(45)计算系统原始残差及各区域综合能源系统对偶残差，判断是否满足收敛判据式(46)，若不满足收敛判据，则返回步骤4；若满足，则输出多区域综合能源系统最优能流结果。

至此，本文提出了一种基于SOCR和自适应步长ADMM的多区域综合能源系统最优能流计算方法。该方法能够有效避免传统模型计算复杂度高，计算时间长，收敛性差等缺陷，并确保模型求解结果的最优性。

3 算例分析

本文选取如图1所示的两区域综合能源系统进行仿真分析，该系统由两个综合能源子系统构成，其中，综合能源系统1由Belgium20气网与9节点配电网连接而成，综合能源系统2由Belgium20气网与7节点配电网连接而成。综合能源系统间通过电网1的节点3与电网2的节点3实现耦合，本算例仅允许配电网1向配电网2提供电功率。Belgium20气网网架参数及负荷数据见文献[18-19]，电网基本参数见文献[20]。采用的系统硬件配置为Inter(R) Core(TM) i7-9750H CPU @2.60 GHz 2.59 GHz，8 GB 内存。操作系统为Win10 64 bit，开发环境为Matlab R2016b，YALMIP 版本为20190425。

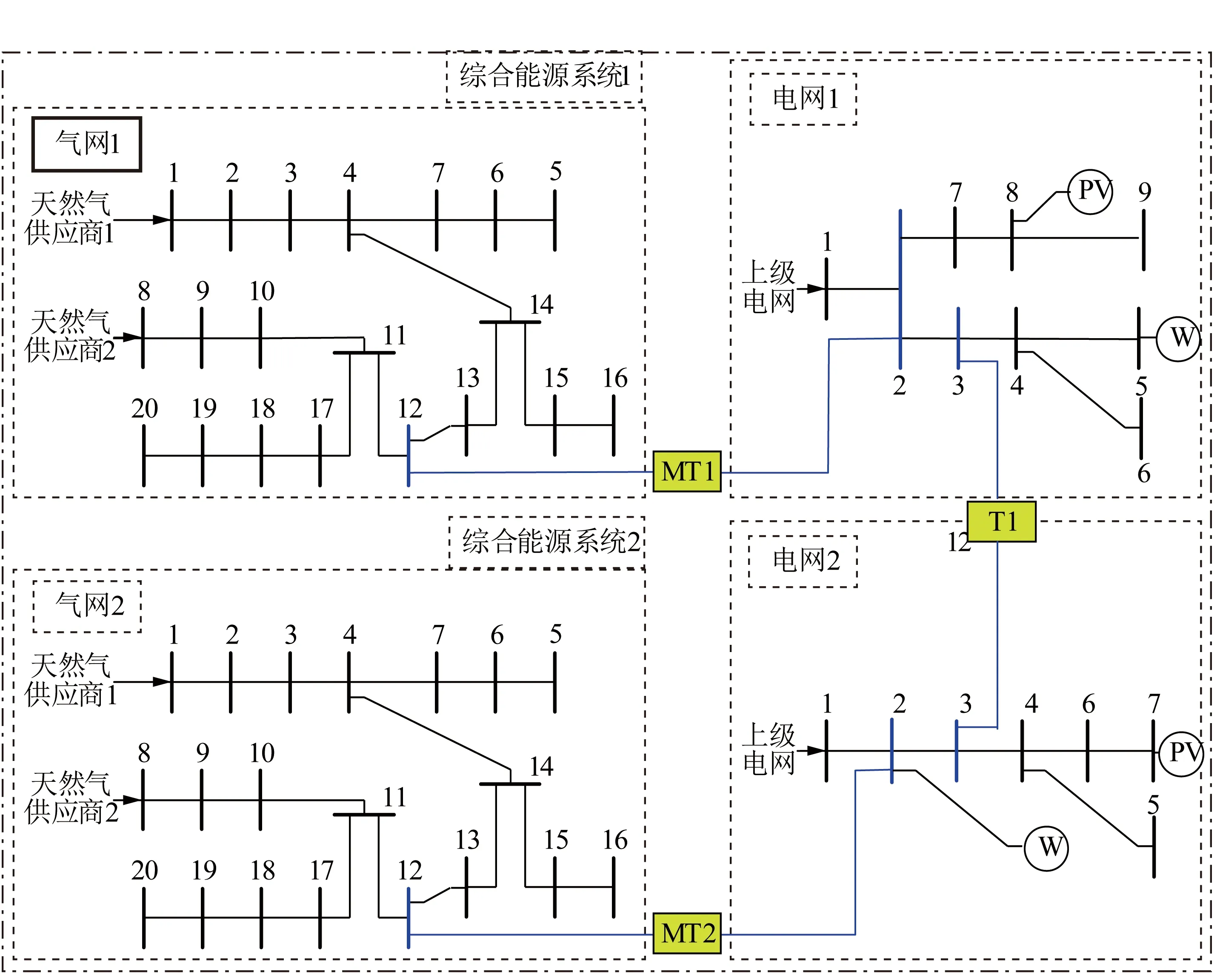
图1 算例结构Fig.1 Structure of the example

本文分别针对计算精度、效率及算法有效性等多个维度进行深入探讨，具体结果如下。

3.1 单时段优化结果分析

首先，为验证本文提出的基于SOCR和自适应步长ADMM算法的多区域综合能源系统最优能流计算方法的求解精度，针对单时段优化问题，将本文算法计算结果与集中式优化算法计算结果进行对比，结果如表1及图2所示。

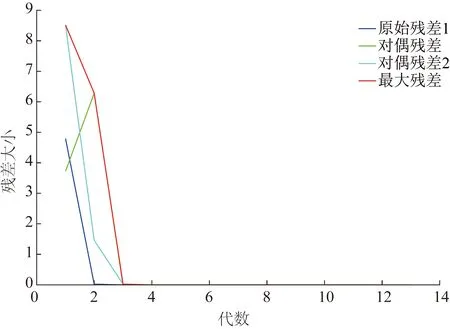
图2 单时段算法残差迭代曲线Fig.2 Single-period residual iteration curve of the algorithm

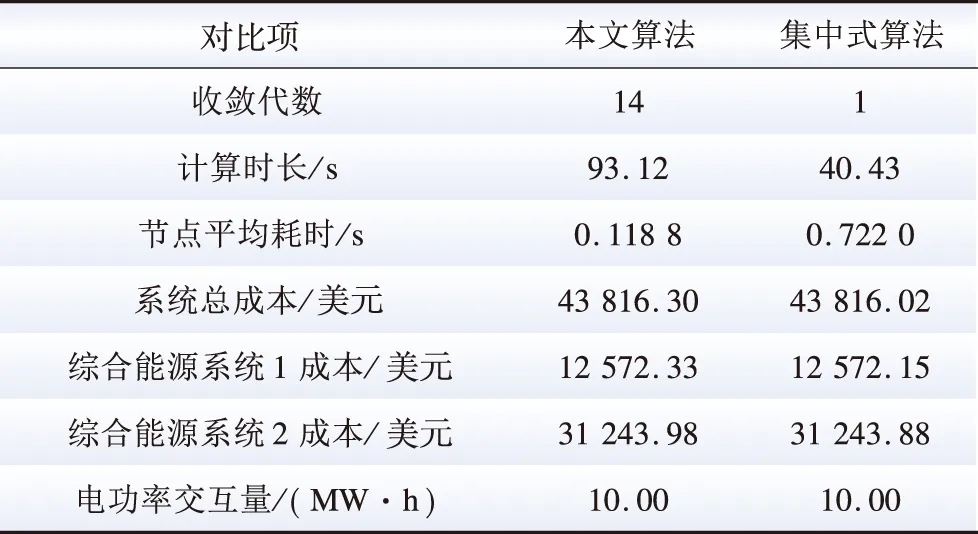
表1 单时段算法对比Table 1 Algorithm comparison in a single period

为比较不同算法的计算效率，进一步引入节点平均耗时指标Tnode[21]：

(47)

式中：T表示算法总计算时间；Cnode表示总计算节点数量。对于串行ADMM算法而言，总计算节点数量为迭代次数与网络总节点数之积。对于串行计算结构，该项指标能够充分表征整个系统的平均节点计算复杂度。

由表1及图2可知，本文所提出的基于SOCR和自适应步长ADMM的最优能流计算计算方法节点平均耗时显著低于集中式算法。与此同时，本文算法优化结果与集中式算法基本保持一致，系统总成本误差低于0.01%，本文算法的计算精度得到有效验证。

3.2 多时段优化结果分析

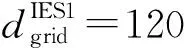
表2 电网2阶梯电价Table 2 Step tariff of grid 2

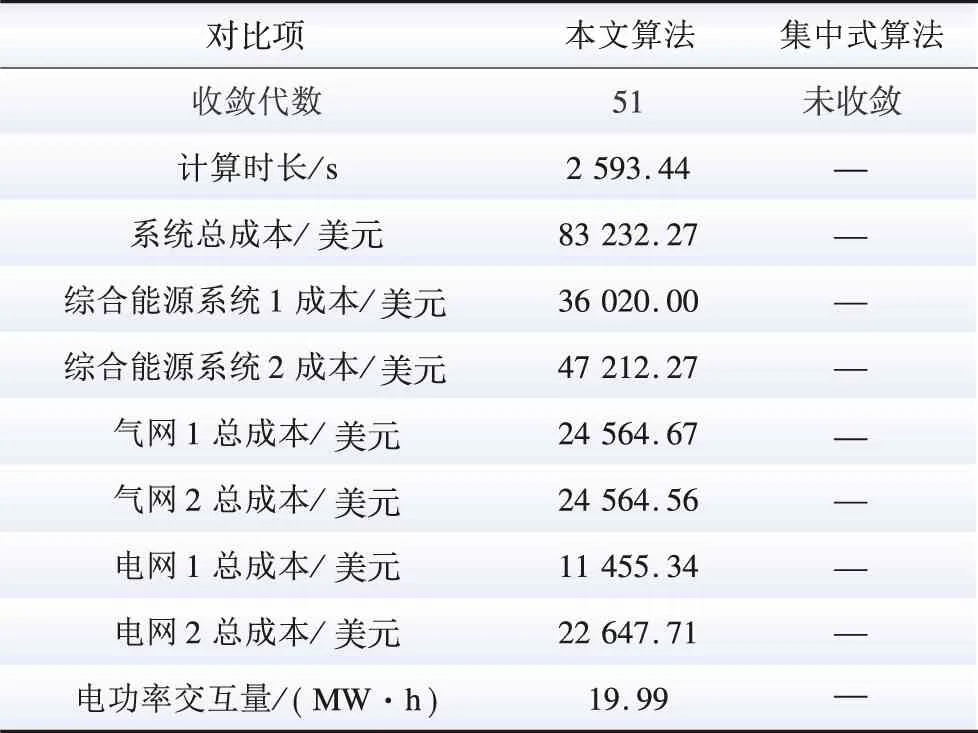
表3 多时段算法对比Table 3 Algorithm comparison of multi-period

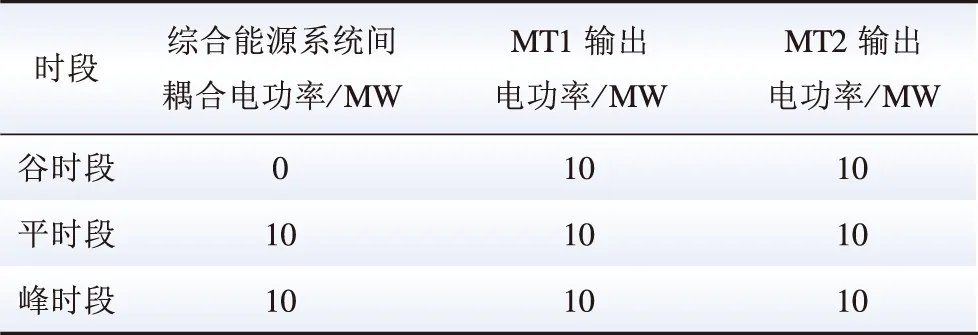
表4 综合能源系统间耦合功率Table 4 Coupling power between integrated energy systems

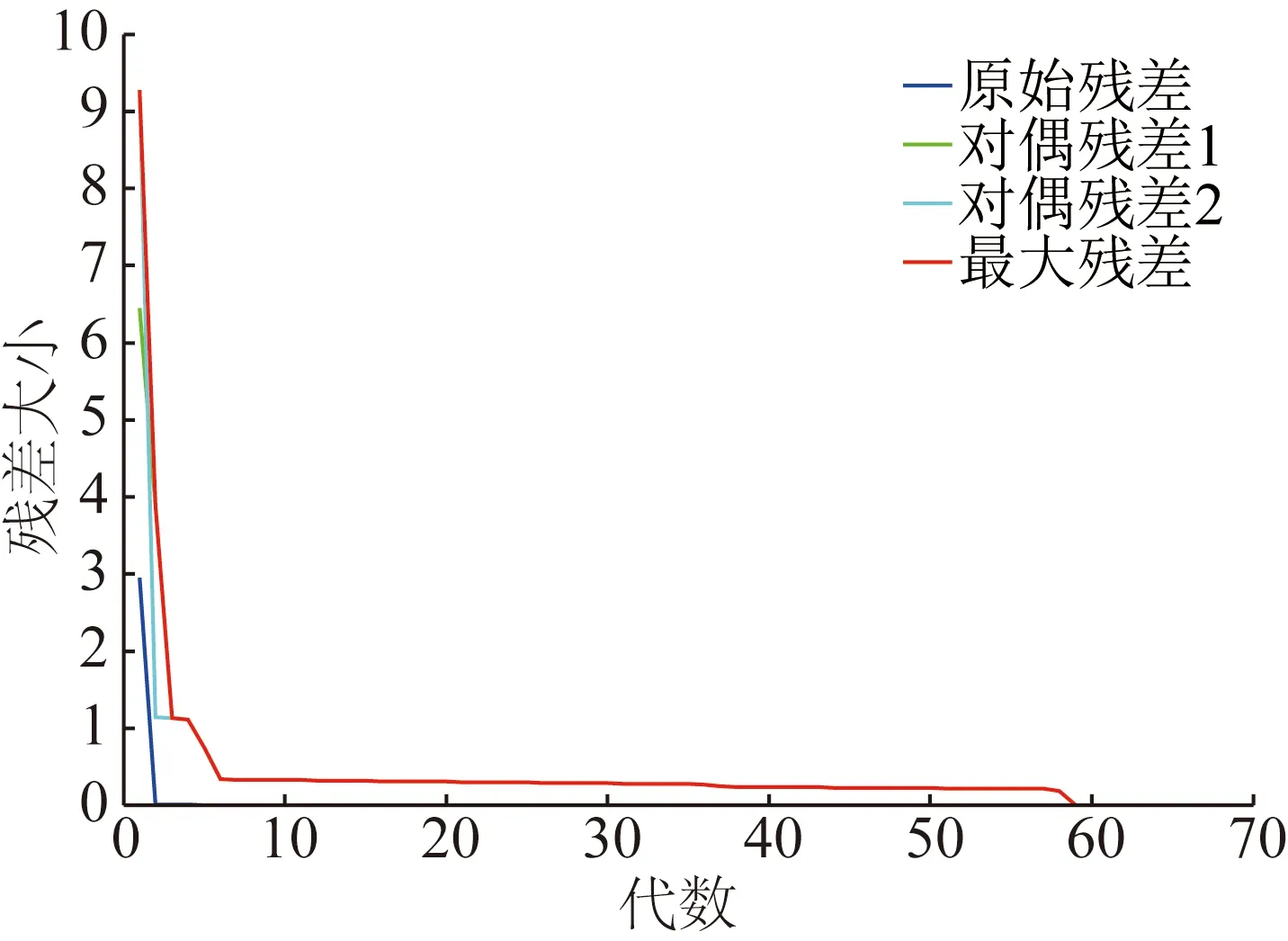
图3 多时段算法残差迭代曲线Fig.3 Multi-period residual iteration curve of the algorithm

由表3、图3和图4可知，由于在多时段场景下模型约束数量显著增加，集中式算法计算复杂度将相应提升，从而导致模型整体不收敛。随着综合能源系统网络规模的进一步扩大，集中式算法计算时间及收敛性将面临严峻挑战。相比而言，本文所提出的基于SOCR和自适应步长ADMM的最优能流计算方法在多时段场景下仍具有良好的收敛性，算法原始残差及各系统对偶残差下降趋势均较为显著，并最终在51代实现收敛。

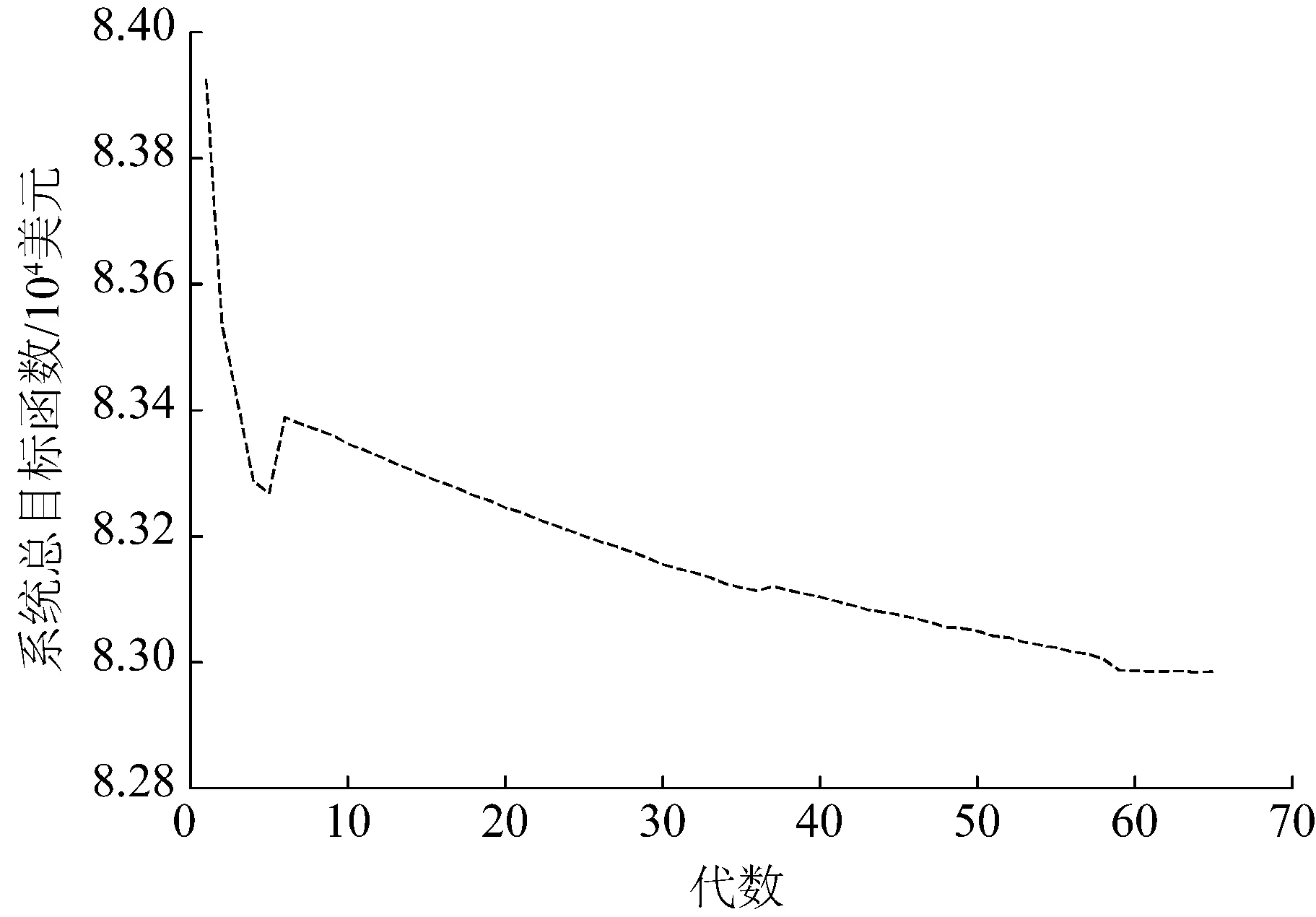
图4 系统总目标函数迭代曲线Fig.4 Iterative curve of the total objective function of the system

由表4可知，由于本算例中气转电价格低于主网购电价格，因此在保证各综合能源系统安全稳定运行的前提下，MT均运行至出力上限点。此外，在谷时段，综合能源系统2电价低于综合能源系统1电价，综合能源系统间交互电功率为0；在峰时段，综合能源系统2电价高于综合能源系统1电价，综合能源系统间交互电功率为支路传输上限；因此，多时段阶梯电价将有效引导综合能源系统间能量交互关系。

4 结 论

本文针对多区域电-气互联综合能源系统最优能流问题，提出了一种基于SOCR和自适应步长ADMM的多区域综合能源系统最优能流计算方法。对比传统算法，本文所提算法能够在确保计算精度的前提下实现多区域综合能源系统最优能流的快速求解，同时，本文算法能够有效避免传统算法在网络规模扩大时所面临的收敛性问题。此外，随着未来综合能源系统间信息数据交互的进一步增强和综合能源系统网络规模的进一步扩大，本文所提多区域综合能源系统最优能流计算方法将具有更加广阔的应用前景。