妙舞“三板斧” 巧破三角函数含参问题
2021-11-17 10:05福建省永春第一中学362600张隆亿
中学数学研究(江西) 2021年11期
福建省永春第一中学 (362600) 张隆亿
根据三角函数的相关性质求解参数的取值或取值范围是三角函数中的一个典型问题.能有效测试学生对三角函数基本性质的掌握程度,难度可控.它受到命题者的青睐.因此,它经常出现在高考题中.此类问题一般涉及范围、单调性和周期性.笔者针对含参数的三角函数问题作如下梳理.
第一板斧:利用单调性求参数的范围
如果解析式中包含参数,则需要根据函数的单调性求出参数的取值范围.通常先求单调区间,再用集合间的关系求解;或者转化为某一方程或不等式,将参数分开,求解析式的取值范围或最大值,再求参数的取值范围.
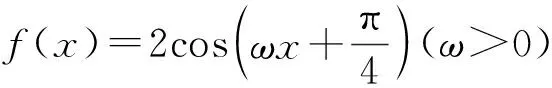

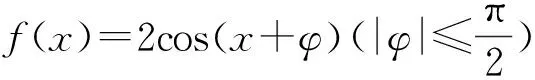

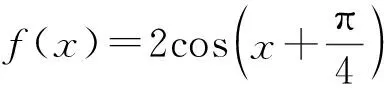
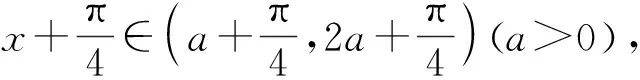
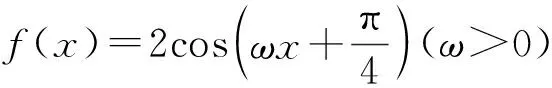

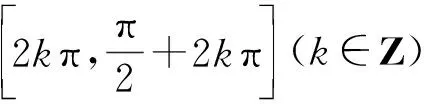
第二板斧:利用对称性求参数范围

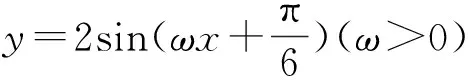
易地移民扶贫,是中国改善贫困人口生产生活环境与条件所采取的一种特殊形式。通过将生产生活条件差或者生态环境脆弱地区的贫困人口,迁移到城镇或其他条件更好的农村。一方面通过易地建设的方式改善受益人群和地区的基础设施和公共服务,同时也相应降低了政府在这些方面投入的建设成本;另一方面通过改变生存环境和提供配套的就业、创收服务,增强了搬迁贫困人口的持续生计能力。
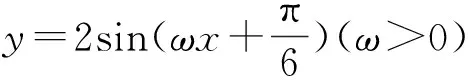
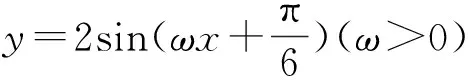
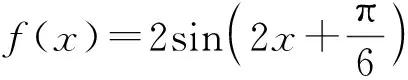
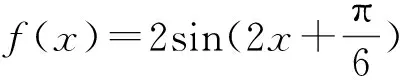

第三板斧:利用相关性质求参数范围
三角函数的周期性决定了三角函数的对称性、单调性、最大值点和零点.反之,三角函数的零点、最大值点、单调性和对称性也可以决定三角函数的周期性.它还影响参数ω的值或范围.解决问题时,应关注相关性质对函数周期影响的性质.
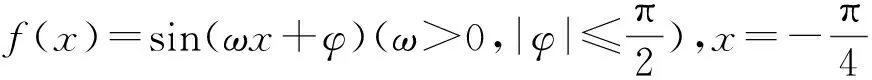
A.11 B.9 C.7 D.5
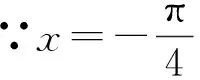

A.4 B.3 C.2 D.1
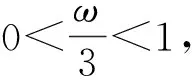
方法归纳:


(3)条件非等价转化时,应注意具体代入检验.
总之,结合对三角函数含参问题的梳理模型化可知,处理含参三角函数问题,往往需要灵活运用“数形结合思想” “等价转化思想”以及“分类与整合思想”,同时需要掌握参数的周期性、单调性、对称性和最值等与三角函数解析式中ω,φ的密切关系,熟悉三角函数基本的性质,可以更有效地解决破解含参三角函数求解过程中的难点.
猜你喜欢
江苏安全生产(2022年8期)2022-11-01
初中生学习指导·中考版(2022年4期)2022-05-12
昆明医科大学学报(2021年8期)2021-08-13
成都体育学院学报(2021年1期)2021-07-16
英语文摘(2020年11期)2020-02-06
幸福·悦读(2018年6期)2018-08-22
中等数学(2018年12期)2018-02-16
新课程·中学(2016年4期)2016-11-19
中学生数理化·八年级数学人教版(2016年6期)2016-08-22
读写算·小学中年级版(2016年5期)2016-05-14

