2021年全国高考乙卷理科数学第12题解法探究
福建省莆田第二中学 (351131) 卢 妮
在近年高考试题中,比较大小问题,如2021年全国高考乙卷理科数学第12题,2020年高考全国卷Ⅲ理科第12题,2020年高考全国卷Ⅲ文科第10题,2019年高考全国卷Ⅰ理科第3题……,对学生来说是个不小的挑战,得分率很低,这一现象引发笔者的思考.为什么学生的解答差强人意?是基础知识薄弱、迁移能力不足、思想方法欠缺,抑或是应试心态紧张?本文从一道2021年高考题谈起,研究这类问题的破解之道.
一、试题呈现
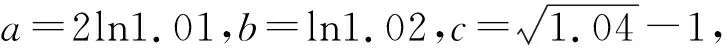
A.a 分析:本题考查比较大小问题,主要考查对数运算、对数函数的单调性、基本不等式等基础知识,考查推理论证能力、运算求解能力、应用意识与创新意识,考查化归与转化思想、分类与整合思想,考查直观想象、逻辑推理、数学运算等核心素养,体现综合性、应用性与创新性. 评析:对于a与c,b与c的大小关系,根据泰勒公式将a,b,c展开估值可得出c与a,b的大小关系. 题1 (2019年高考全国卷Ⅰ理3)已知a=log20.2,b=20.2,c=0.20.3,则( ). A.a 分析:运用中间量0比较a,c,运用中间量1比较b,c,故选B. A.a 题3 (2020年全国卷Ⅲ理12)已知55<84,134<85.设a=log53,b=log85,c=log138,则( ). A.a 波利亚指出:“数学问题的解决仅仅只是一半,而更重要的是解题之后的回顾与反思.”本文中研究的题目考查比较大小问题,难度较大,关键难点是将各个值中的共同的量用变量替换,构造函数,利用导数研究相应函数的单调性,进而比较大小,这样的问题,凭借近似估计计算往往是无法解决的.而高考链接题1-4不尽相同,但其题目背景都是以“对数式”为载体,解题目标均是“比较大小”,比较的方法均可利用“不等式传递性”,解题思想均是“化归与转化”.这启示教师在解题教学中可通过一题多解,多个角度分析一道题目的思路,让学生领会其中渗透的思想方法,积累解题经验,达到“做一题、通一类”的效果.二、解法分析
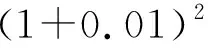
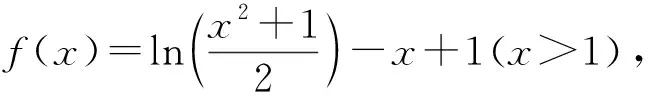

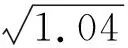
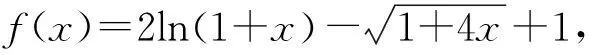

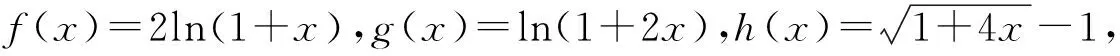
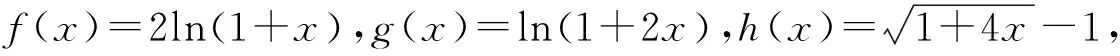
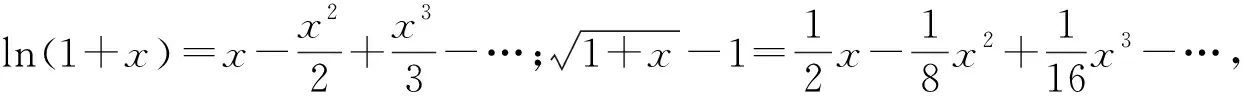
三、链接高考
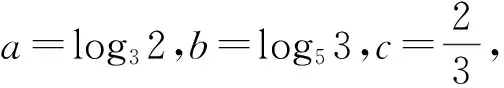

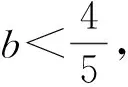
四、回顾反思

