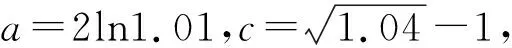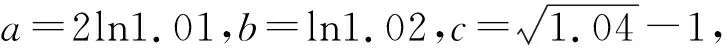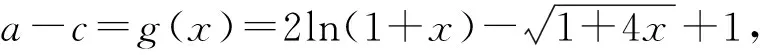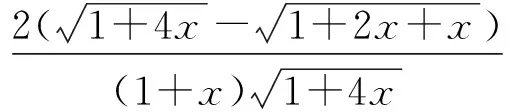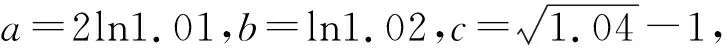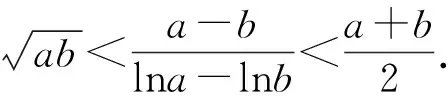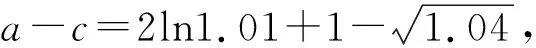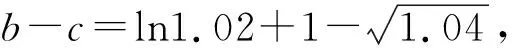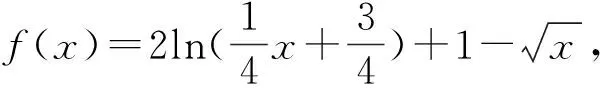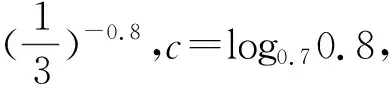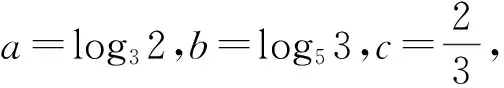比较大小有门道，广泛联系巧构造

陕西省煤炭建设公司第一中学 (727000) 徐海军

陕西省汉中市四〇五学校 (723312) 侯有岐

A.a

比较大小主要考查对函数知识的综合运用能力，是高考常考题型之一.本题条件简洁，a，b，c三数相差微乎其微，可以说除了构造函数再无其它妙法.那么如何构造函数呢?因为三数a，b，c的结构差异很大，无法用同一函数统一起来.但是利用对数的运算和对数函数的单调性或者贝努力不等式不难对a，b的大小作出判定,而对于a与c，b与c的大小关系，则需根据其结构特点构造不同的函数来比较大小.

(1)先比较a与b的大小.

思路一：利用对数运算和对数函数单调性.

解法1:根据对数的运算可知a=2ln1.01=ln1.012=ln1.0201，又b=ln1.02，由对数函数的单调性得a>b.

思路二：利用贝努力不等式(1+x)α≥1+αx(α≥2,x>-1).

解法2:由解法1知比较a与b的大小关键在于比较(1+0.01)2与1.02的大小，事实上，由贝努力不等式(1+x)α≥1+αx(α≥2,x>-1)，易得(1+0.01)2>1+2×0.01=1.02，由对数函数的单调性得a>b,这样就排除了选项A,D,下来的任务关键就是判定a与c，b与c的大小关系.

(2)比较a与c,b与c的大小.

思路一：构造函数，利用函数单调性比较大小.

对于a与c,b与c的大小关系，可以将0.01或0.02换成x，分别构造函数，利用导数分析其在0的右侧较小范围内的单调性，得出a与c,b与c的大小关系.

综上所述，b

综上所述，b

思路二：利用对数平均不等式比较大小.

综上所述，b

思路三：用待定系数法确定函数解析式，利用函数单调性比较大小.

用待定系数法确定函数解析式，将未知部分试用最简单的一次函数代换，将有根号的部分用二次函数代换，从而确定函数解析式，最后利用得到的函数单调性解决比较大小问题.

回顾本题的解法，我们有如下的思考：

1.比较大小的问题，常见方法有临界值法、单调性法、构造函数法等三种.

2.比较大小中比较复杂的问题，一般都可以通过构造函数，转化为利用函数的单调性解决，在此导数是通法.

同理，比较b与c的大小，也可以仿照思路三的解法5，用待定系数法得到解决.由于篇幅所限，下列类似高考题请读者练习.

1.(2020全国卷Ⅰ理12)若2a+log2a=4b+2log4b，则( ).

A.a>2bB.a<2bC.a>b2D.a

2.(2020全国卷Ⅱ理11文12)若2x-2y<3-x-3-y，则( ).

A.ln(y-x+1)>0 B.ln(y-x+1)<0

C.ln|x-y|>0 D.ln|x-y|<0

3.(2020全国卷III理12)已知55<84,134<85.设a=log53,b=log85,c=log138，则( ).

A.a

C.b

A.a

C.b

A.a

C.b

(答案分别为B，A，A，D，A)