一道抛物线高考题的解法探究及推广

新疆教育科学研究院 (830049) 晏 鸿

新疆乌鲁木齐市实验学校 (830026) 符强如

一、题目呈现

已知抛物线C：x2=2py(p>0)的焦点为F，且F与圆M：x2+(y+4)2=1上的点的距离的最小值为4.(1)求p；(2)若点P在M上，PA，PB是C的两条切线，A、B是切点，求△PAB面积的最大值.

这道题是2021年高考乙卷理数21题，从问题表述来看，此题取材平实, 表现朴实, 题干清晰，传承了全国卷高考命题简约、稳健的风格.从内容上来看考察抛物线切线、直线和圆锥曲线平面图形(三角形)面积问题.它考查了考生的逻辑推理、数学建模、数学运算等核心素养，要求考生需要具备较高的思维能力，不愧起到了压轴的功能.

二、第(2)问解法探究

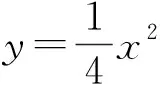
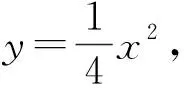
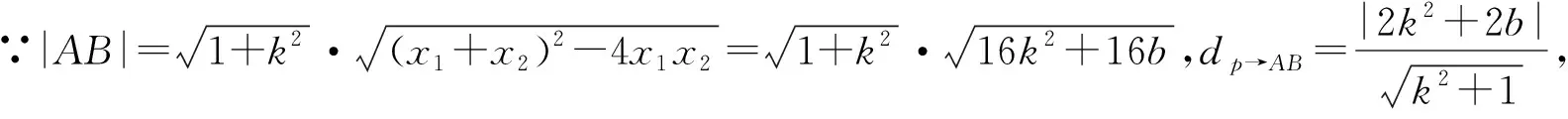
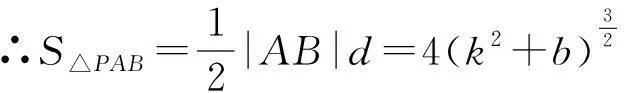
评注：解法1中对直线AB中引入了斜率和纵截距，将面积转化为了k、b的函数.思考是否可以从减少变量的角度出发，将面积用点P坐标去表示或者根据图形来寻找关系表示面积，减少运算，优化解法.

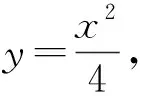
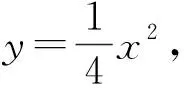
思路二：运用参数方程能够快速解决我们圆锥曲线的弦长，范围等问题，其核心就是减少了变量或参数，此题可以借助抛物线参数方程和圆的参数方程大大优化云算.

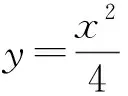
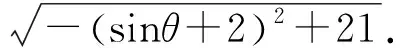
三、探究推广

笔者经过探究，发现上述问题结论可以一般化并推广，可得到如下结论：

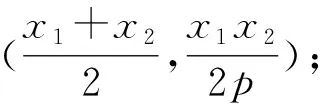
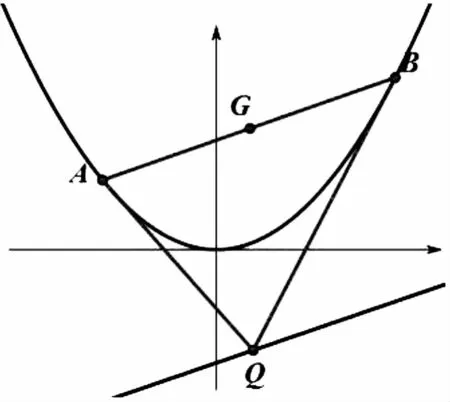
图1

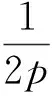
从题目出发追本溯源, 可以完善知识系统的建构, 有利于学生逻辑思维的训练.探究问题要着眼于知识要点, 注重知识联系, 从而拓展知识广度，方能拓展解题思路, 凸显数学高度[1].阿基米德三角形还有很多性质，这里就不一一举例，与本题相关联性质大致还有四个，其证明思路与前面大致相同，读者感兴趣可自行证明，此处从略.

性质1 过抛物线x2=2py上任意一点

A(x0,y0)的切线方程为xx0=p(y+y0).

性质2 已知Q是抛物线准线x2=2py上任意一点，过Q作抛物线的切线QA、QB分别交抛物线于A、B两点，则AB过抛物线的焦点且AQ⊥BQ.

性质3 设过点Q与抛物线对称轴平行的直线交抛物线于M，交切点弦于点P，则P点平分切点弦AB.(无论点Q在曲线的什么位置，上述结论均成立).且M处的切线平行于抛物线的切点弦.

性质4 点Q为直线l:y=kx+m上一动点，过点Q引抛物线x2=2py两条切线QA，QB，则过两切点的直线AB必过定点G(pk,-m).

读者不妨尝试用以上方法解下面这道高考压轴题.