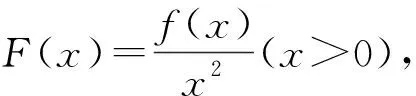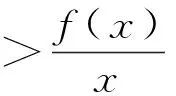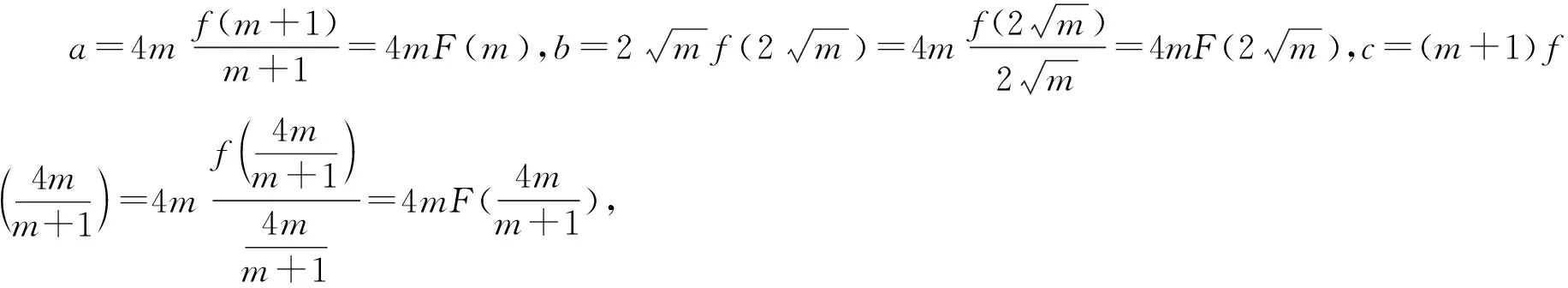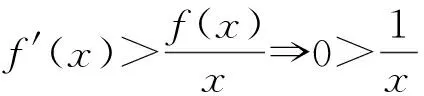以抽象函数为背景的不等式问题再探究
福建省厦门双十中学 (361015) 梁莹莹
以抽象函数为背景的不等式问题,既能综合考查函数的求导法则、图像与性质,又能考查学生转化变形与联想构造的思维能力,因此备受命题专家的青睐,常在客观压轴题的位置出现.就此类难点问题主要有结构化、同构化、特殊化三种破解策略[1],本文例析对该问题的进一步拓展探究.
1.在函数与导数知识模块中的纵向延伸
例1 已知函数f(x)的定义域为R,其图像关于点(1,0)中心对称,其导函数为f′(x),当x<1时,(x-1)[f(x)+(x-1)f′(x)]>0,则不等式xf(x+1)>f(2)的解集为.
解法1:(结构化策略)当x<1时,x-1<0,条件不等式转化为f(x)+(x-1)f′(x)<0,构造函数F(x)=(x-1)f(x),则F′(x)=(x-1)f′(x)+f(x)<0⟹F(x)在(-∞,1)上单调递减,因f(x)和x-1的图像都是关于点(1,0)中心对称,则F(x)=(x-1)f(x)的图像关于直线x=1轴对称,故F(x)在(1,+∞)上单调递增,由此可知G(x)=F(x+1)=xf(x+1)为偶函数,目标不等式变形为G(x)>G(1),综合单调性和奇偶性可得|x|>1⟹x∈(-∞,-1)∪(1,+∞).
解法2:(特殊化策略)构造关于点(1,0)中心对称的一个特殊函数f(x)=x-1,也满足当x<1时,f(x)+(x-1)f′(x)=2(x-1)<0,所以目标不等式xf(x+1)>f(2)可化为x(x-1+1)>1,易求得解集为(-∞,-1)∪(1,+∞).
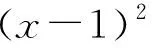
例2 已知函数f(x)的导数为f′(x),f(x)不是常数函数,且(x+1)f(x)+xf′(x)≥0,对x∈[0,+∞)恒成立,则下列不等式一定成立的是( ).
A.f(1)<2ef(2) B.ef(1) C.f(1)<0 D.ef(e)<2f(2) 解法1:(结构化策略)原式等于xf(x)+f(x)+xf′(x)=xf(x)+[xf(x)]′≥0,设F(x)=ex[xf(x)],那么F′(x)=ex[xf(x)]+ex[xf(x)]′=ex[xf(x)+[xf(x)]′]≥0,所以函数F(x)=ex[xf(x)]是单调递增函数,F(1) 解法2:(特殊化策略)不妨设f(x)=x,则(x+1)f(x)+xf′(x)=(x+1)x+x=x(x+2)>0对x∈[0,+∞)恒成立,则f(1)=1,f(2)=2,f(e)=e,代入四个选项,可得(A)1<4e,(B)e<2,(C)1<0,(D)e2<22,可用排除法快速选出正确答案为A. 总结反思:本题的难点是条件中(x+1)f(x)+xf′(x)≥0这个不等式的复杂性,它并不满足前面总结的那些结构类型,但是对此不等式展开变形得到xf(x)+f(x)+xf′(x)≥0,其中先对后面两项做处理xf(x)+f(x)+xf′(x)=xf(x)+[xf(x)]′≥0,再把xf(x)看成一个整体函数,比如设g(x)=xf(x),则g(x)+g′(x)≥0⟹exg(x)+(ex)′g(x)=[exg(x)]′≥0,因此构造函数F(x)=ex[xf(x)],这种“嵌套式”两次构造函数的方法运用了整体思想,对学生提出更高的能力要求.而用特殊化策略,构造简单的具体函数f(x)=x,则大大降低了问题的难度,化解了难点. 例3 定义在R上的函数f(x)的导函数为f′(x),f(0)=0,若对任意x∈R,都有f(x)>f′(x)+1,则使得f(x)+ex<1成立的x的取值范围为( ). A.(0,+∞) B.(-∞,0) C.(-1,+∞) D.(-∞,1) 例4 设f′(x)是函数f(x)(x∈R)的导数,且满足xf′(x)-2f(x)>0,若A,B,C是锐角三角形ABC的三个内角,则( ). A.f(sinA)sin2B>f(sinB)sin2A B.f(sinA)sin2B C.f(cosA)sin2B>f(sinB)cos2A D.f(cosA)sin2B 解法2:(特殊化策略)不妨设f(x)=-1,则xf′(x)-2f(x)=2>0恒成立,则A,B选项具体化为-sin2B>(或<)-sin2A,C,D选项具体化为-sin2B>(或<)-cos2A,由cosA A.a C.b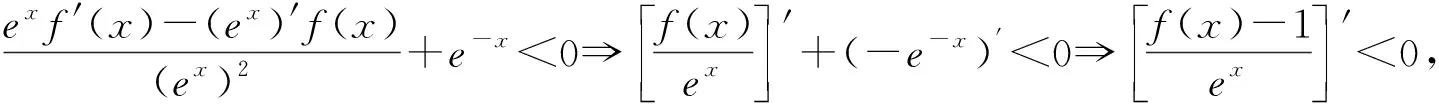
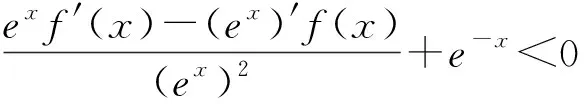
2.与其他知识模块的横向联系