基于改进谱聚类的人群移动行为检测

杨玉成，张 乾，2，邵定琴，岳诗琴

(1. 贵州民族大学数据科学与信息工程学院，贵州 贵阳 550025；2. 贵州省模式识别与智能系统重点实验室，贵州 贵阳 550025)

1 引言

公共场所人群密度越来越高，例如机场、火车站、公园、旅游区等，大量人群聚集和离散容易引起安全事故的发生，因此公共场所人群事件实时监测变得越来越重要[1]。传统人群监测方法需要人工实时观察视频情况，导致公共场所人群事件监测效率低[2]。为了提高人群监测效率、降低监测成本。通过借助计算机分析公共场所人群移动行为，自动检测和识别公共场所存在的异常行为，从而提高公共场所的安全防控效率，因此人群移动行为检测成为模式识别、机器学习、计算机视觉等领域研究的新问题。

在人群移动行为检测中，虽然已经出现许多理论知识和检测方法，但是仍然存在许多技术难题：①人群移动会伴随跳跃、奔跑、肢体扭动等带来的不确定性影响因素[3]；②拥挤场景中的人群存在严重遮挡、倒影等噪声；③在时域和空域对人群移动行为进行分析[4]；④人群移动过程中，人群密度、形状、边界等随时间不断变化[5]。同时群体移动行为检测比个体移动行为检测难度大，群体移动行为表现为一种高层次的语义互动[6]，为人群行为分析建模带来巨大挑战[7]。

2 群体研究

群体行为是生物界中一种极为普遍的现象，生物群体研究主要分为两个领域：①宏观领域；②微观领域。宏观领域主要针对人群、鱼群、羊群、鸟群等群体进行研究[8]；微观领域主要针对菌落进行研究。随着人们对公共安全关注度的不断提高，人群移动行为分析成为热点问题。人群移动行为分析分为社会学范畴和计算机视觉的研究；在社会学范畴中，个体的运动往往与周围群体存在一定联系[6][8-10]，个体行为会受到周围人群的影响，即在群体活动中不存在个体自主行为；在计算机视觉领域中，大多数研究将群体结构进行细化，从个体之间的相互作用出发，将个体之间的社会关系进行空间量化，从而对群体移动行为进行客观描述，同时对存在不同社会关系的人群进行检测分析。在计算机视觉领域中，经过长期发展与积淀，出现许多经典的人群移动行为检测方法。人群移动行为检测方法分为：①基于群体组的检测方法；②基于视图的检测方法。

基于群体组检测的方法包括：①粒子法；②轨迹分析法[10]。粒子法是通过观察图像上驱动粒子的流动来检测人群移动，Mehran等人[11]通过社会力模型应计算粒子之间的相互作用力，根据作用力大小对人群异常区域进行定位；Raghavendra等人[12]采用粒子群算法对社会力模型进行优化，并通过分割算法对人群异常区域进行分割；Ullah等人[13]提出一种流体动力学模型对人群进行检测。轨迹分析法是对人群移动轨迹进行聚类分析，Cui等人[14]采用K-means算法对人群移动轨迹点进行聚类，从而将人群分成不同的群组；Mousavi等人[15]提出一种增强定向轨迹直方图方法，对公共场所异常人群进行检测。Zhou等人[16]提出一种混合动力模型模拟人群行为，再通过移动轨迹判断人群在过去某时刻的行为和预测即将发生的行为。虽然基于群组检测的方法能够检测到场景中的不同人群，但是由于人群处于不断移动的状态，群组形态随时间不断不断变化，因此群组关系难以确定，导致该类方法检测精度不高。

基于视图的检测方法主要是对视频图像进行聚类，视图聚类又分为单视图聚类和多视图聚类。Peng等人[17]针对场景中人群存在遮挡问题，提出一种贝叶斯网络模型，用于多摄像头人群检测。Li等人[18]设计一种人群移动的个体结构特征，并提出一种自加权多视图聚类方法对个体结构特征进行聚类，随后Wang等人[10]又提出一种基于自加权多视图聚类的人群检测框架。虽然该类方法可对场景中的人群进行有效聚类，但是该类方法需要通过先验知识设定阈值，并且算法结构、参数较多，所以该类方法在实际应用中难以实现。

针对上述问题，本文对谱聚类算法进行改进，提出一种基于改进谱聚类的人群移动行为检测算法。首先构造一种新的邻接矩阵作为谱聚类算法的输入参数；然后构造一种新的拉普拉斯矩阵，并随机选取拉普拉斯四个特征值组成特征向量，最后采用K-means算法对特征向量进行聚类得到人群簇。通过在各大国际公开数据集进行实验，结果证明了本文提出算法的有效性。

3 谱聚类算法

谱聚类算法是一种基于图论的聚类方法，该算法具有结构简单、计算量小、容易实现、鲁棒性强等优点，在对复杂数据聚类时，也能得到较高聚类精度。因此本文采用谱聚类算法对人群进行聚类。

在谱聚类算法中，将人群场景图像视为一张无向加权图I(λ，E)，其中λ是数据点λ1，λ2，…，λn的集合，E是连接任意两个数据点的连接线e1，e2，…，en的集合，ωi，j(i，j∈λ)是e1，e2，…，en所对应的权值[20]，即i，j两点的相似度，具体定义为

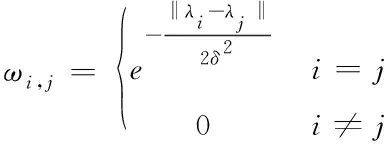
(1)

由此可得到相似度矩阵W∈Rn×n，而度矩阵D则定义为

(2)

由相似度矩阵W和度矩阵D可构建拉普拉斯矩阵L∈Rn×n，其具体定义为[20]

(3)

在实际数据聚类过程中，还需对拉普拉斯矩阵L进行标准化，标准化后的拉普拉斯矩阵为

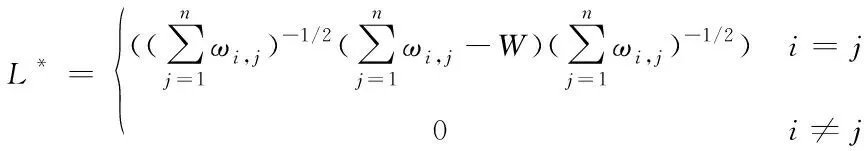
(4)

对标准化后的拉普拉斯矩阵L*求K∈R个特征向量F=(f1，f2，…，fk)，其中K的大小为类别数。再次对由K1个特征向量F进行标准化后得到一个n×k1维的特征矩阵M，然后选择聚类算法对矩阵M进行聚类，得到聚类维数K2，即K2为人群类别数。

4 人群聚类

人群在移动过程中会产生时空相关结构，这种结构被称为集体流形[8]。在文献[8]中首先定义个体行为在其邻域内的相似性，即行为一致性。当个体j在邻域i中，在t时刻j∈N(i)时，相似性定义为

(5)

其中δt(i，j)∈[0，1]，Ct(i，j)是i和j在t时刻的速度相关系数。由于当i和j为两个独立个体时，即不在同一邻域内的两个个体之间，其行为存在不确定性，长度为l的路径行为相似性定义为

υl(i，j)=υγl1(i，j)+υγl2(i，j)+…+υγln(i，j)

(6)

其中pl为所有长度为l的路径集合，γlk∈pl(k=1，2，…，n)为特定路径，υγlk(i，j)为特定路径γlk的相似性度量。式(6)为长度为l的路径相似度，则在l的尺度上将i的集体性定义为

ψl(i)=υl(i，c1)+υl(i，c2)+…+υl(i，cn)

(7)

其中cn为个体。由此得到群体集体性

ψl=E((ψl(i))

(8)

为将所有路径上的个体集体性与群体集体性进行拟合，因此定义一个生成函数用于度量总体相似性

φi，j=z1υ1(i，j)+z2υ2(i，j)+…+znυn(i，j)

(9)

其中zn为路径的权重。在给出了群体相似性和群体集体性的度量定义，在此基础之上可得到一个η矩阵

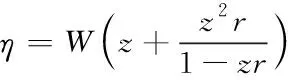
(10)

其中W是邻接矩阵，r是拓扑范围，对η进行阈值化处理，去除集体性较低的粒子保留集体性较高的粒子，将运动中的群体划分为不同类。

5 本文算法

为解决场景中移动人群存在遮挡和倒影问题，本文提出一种基于改进谱聚类的人群移动行为检测方法。首先，本文提出一种邻接矩阵构建方法和拉普拉斯矩阵构建方法，将邻接矩阵作为谱聚类的输入参数；然后，随机选取拉普拉斯矩阵的四个最小特征值组成特征向量；最后，通过K-means算法对特征向量进行聚类，得到人群聚类数。

5.1 邻接矩阵

在构造邻接矩阵之前需要构建一个相似性矩阵，其中相似性矩阵的构建方法主要有三种[19]：

1)ε-邻接法，相似性矩阵定义为

(11)

其中ε为个体间的距离，由于所有dij值都相同，因此ε-邻接图法被称为未加权相似性矩阵。

2)k-最近邻法，相似性矩阵定义为

(12)

其中U(i，j)是i和j的邻域。

3)全连接法，相似性矩阵定义为

(13)

其中ωk∈ωi，j。

由上述三种方法定义的相似性矩阵信息损失较多。式(6)为文献[8]定义路径相似度矩阵，由此可得到度矩阵

(14)

由D(i，j)得到邻接矩阵M(i，j)，则邻接矩阵可以表示为[8]

M(i，j)=υl(i，j)×M(i，j)

(15)

由式(15)得到的邻接矩阵是一个奇异矩阵，在计算时无法得到确定值，从而导聚类失败，针对这一问题本文把式(15)进行改进，把邻接矩阵定义为

M1(i，j)=[υl(i，j)×M(i，j)]+I1(i，j)

(16)

其中I1(i，j)为一个元素全为1的矩阵。本文将式(16)作为谱聚类算法的输入。

5.2 K-means聚类

K-means算法在数据聚类中表现出优越的性能，在对复杂数据进行聚类时也能得到较高聚类精度，因此本文采用K-means算法作为谱聚类的聚类模块。

在数据聚类中，K-means将属于同一类中的数据点间距离最小化，将不同类之间的数据点距离最大化。在人群聚类中，将人群划分为C={C1，C2，…，Ck}，Ck∈N*，Ck∈Ν*，所有人群中的个体间距离均值为

(17)

其中dc为距离之和，由式(17)可得到人群的聚类函数[20]

(18)

其中cin为任意人群，xcin为任意人群cin的个体数。

在得到K-means算法的聚类函数之后，需要构建拉普拉斯矩阵作为输入参数。本文提出一种拉普拉斯矩阵构造方法，即定义拉普拉斯矩阵为

L(i，j)=I(i，j)-D(i，j)-M1(i，j)

(19)

其中I(i，j)为一个单位矩阵，在得到拉普拉斯矩阵之后，首先，随机选取拉普拉斯矩阵的四个最小特征值组成特征向量；然后，通过人群聚类函数(式(18))对特征向量进行聚类，得到人群聚类数；最后，聚类结果将人群聚类数映射至视频帧图像，实现对场景中移动人群聚类。

5.3 改进谱聚类人群检测算法

为更加形象说明本文提出算法的实现过程，因此绘制了本文算法结构流程图。算法结构流程如图1所示。

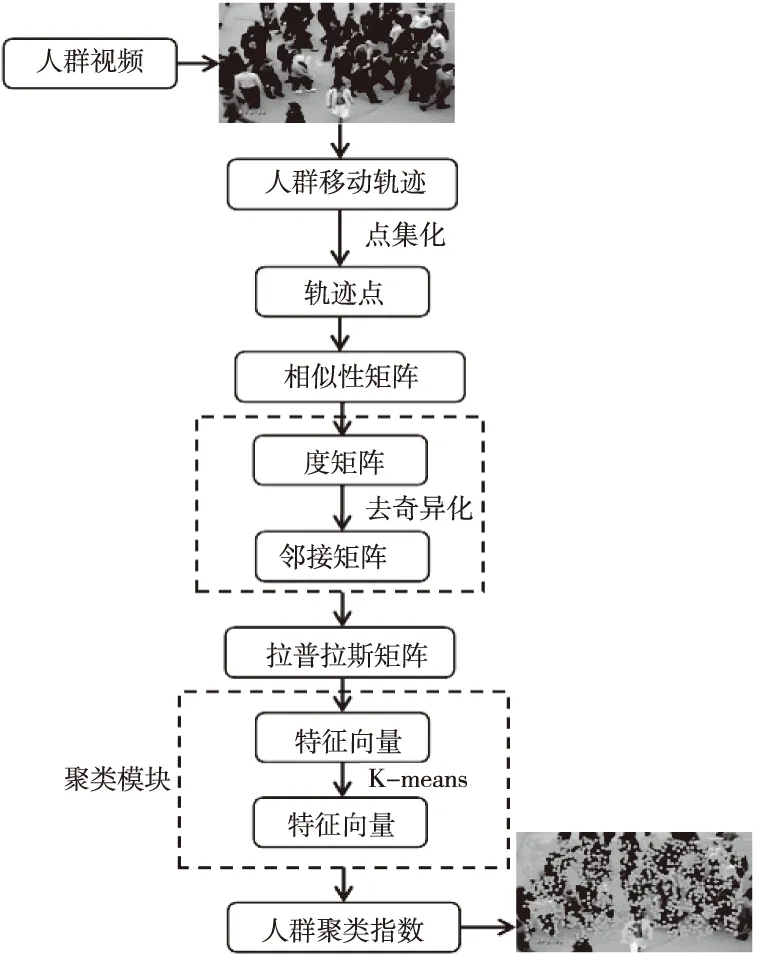
图1 改进谱聚类算法

6 实验结果与分析

本文提出改进谱聚类人群移动行为检测算法，为验证本文提出算法的有效性，本文通过在CCD(CUHK Crowd Dataset)[21]，CMD(Collective Motion Database)[8]，MPT(MPT-20×100)[9]三个数据进行验证，选取ROC、AUC、Entropy、Purity、F-Measure指标，并与CF(Coherent Filtering)[22]，MCC(Measuring Crowd Collectiveness)[8]算法进行对比。实验结果表明，本文算法具有更好的聚类性能。

6.1 聚类评价

本文采用谱聚类算法对场景人群进行聚类，首先提出一种新的邻接矩阵和拉普拉斯矩阵，然后选取拉普拉斯矩阵的四个最小特征值组成特征向量，最后通过K-means算法对特征向量进行聚类。为综合评价本文提出算法的有效性，将本文算法与其它算法在各种公开数据集上进行实验对比。

图2为本文算法与其它算法在CCD、CMD、MPT三个国际公开数据数据集上的人群聚类视觉效果，其中不同颜色所覆盖的区域代表不同的人群。由聚类结果可知，本文提出算法可对不同场景中不同密度的人群进行有效聚类，并能够检测到场景中的所有人群，实验结果表明，本文提出算法具有优越的人群检测性能和人群聚类性能。

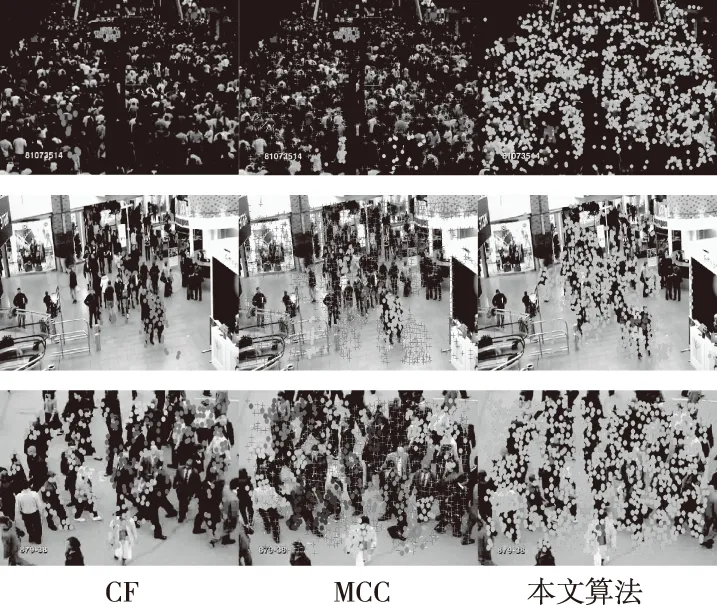
图2 人群聚类效果

表1统计了本文算法与其它算法对场景中人群的检测点数，本文提出算法所检测到的点数比CF算法高618个点，比MCC算法高178个点，结果表明本文提出算法能够检测场景中的大多数人群，证明了本文算法优越的检测性能。

表1 各种算法聚类指标

6.2 算法对比

为综合证明本文提出算法的优越性能，将本文提出的改进谱聚类算法与其他人群聚类算法在CCD数据集上进行实验，并对比人群聚类纯度(Purity)和FM值(F-Measure)指标。

表1为本文提出的改进谱聚类算法与其他人群聚类算法在CCD数据集上的各项指标值。加粗部分为本文算法所得结果，本文算法的Purity值比MCC算法高0.067，F-Measure值比MCC算法高0.16，虽然本文算法的Purity值比CF算法低0.042，但是本文算法的F-Measure值比CF算法高0.093，这些结果都证明了本文提出算法的有效性。

为进一步证明本文算法的有效性，对本文提出的改进谱聚类算法和其他人群聚类算法进行AUC值、人群检测数、聚类数对比。表2为各种算法的聚类AUC值，加粗部分为本文聚类结果的AUC值，本文提出算法的AUC值比CF算法高0.111，比MCC算法高0.004。

表2 各种算法AUC值

表3统计了本文提出的改进谱聚类算法与其他人群聚类算法对场景中人群的检测点数，本文提出的改进谱聚类算法所检测到的点数比CF算法高618个点，比MCC算法高178个点，结果表明本文提出算法能够检测场景中的大多数人群，证明了本文算法的有效性。

表3 各种算法人群检测数

图3为统计了本文提出的改进谱聚类算法与其他人群聚类算法的人群类别数，本文提出算法对人群聚类所得类别数与groundtruth最接近，仅比groundtruth高出1个类别，CF算法比groundtruth高出2个类别，MCC算法比groundtruth高出10个类别。这进一步证明了本文算法的有效性。

图3 各种算法聚类数

7 结论

针对人群场景人群存在遮挡和倒影问题，本文提出一种改进谱聚类的人群移动行为检测方法。首先构造一种新的邻接矩阵和拉普拉斯矩阵，将构造的邻接矩阵作为谱聚类的输入参数，然后选取拉普拉斯矩阵的四个最小特征值组成特征向量，最后采用K-means算法对特征向量进行聚类，通过在公开数据集数据集上进行实验，并与目前主流算法进行对比。本文通过对实验结果的定性和定量分析，结果证明了本文提出算法的有效性。在未来研究工作中，将继续探索人群移动行为检测算法的创新与优化。