基于结构方程模型的小学数学课堂教学实证研究
江爱柳
(福建省南平市政和县南门小学 福建 政和 353600)
所谓方程,其实指的就是两个数学公式之间构建未知数和已知数等号关系的数学模型。而学生在建构方程模型的过程中,需要通过数学基础概念和数学公式以及数学具体内容对方程的数学模型进行深入探究,且解答出公式的真正含义和现实问题的关键。分析方程价值的过程,除了要对方程浅层上的意义进行理解以外,还要对方程深层上的本质特性进行剖析。而浅层上的意义指的就是带有未知数的相等公式。深层上的意义指的则是已知数和未知数之间形成的等量关系。教学工作者可以先从现实生活当中的实例讲解,让学生基于自身的知识基础把问题当中等量关系提炼出来,使学生对于等号的认知不再停留在计算结果的意义之上,而是了解等号起到的桥梁作用。
1.创设天平情景,直观认知方程模型
方程模型的学习过程,就是学生感知建构模型的过程。对于小学生来说,方程模型的学习过程较为复杂,所以教学工作者在讲述方程模型的时候,可以先从学生们熟知的场景当中,提炼出符合方程模型教学的材料,并激活学生对于已知概念和公式的记忆力,继而引导学生对记忆里的知识点进行运用。教学工作者之所以要创设出一个天平的情景,是因为天平的两端呈现出的是物质双方的等量关系。且它能够把抽象的方程模型直观地显现出来,学生可以通过这种平衡,深入理解等量和非等量的具体内涵,并在建构起方程模型之后,用算式的方法表达出等量关系的含义。
以小学数学北师大版第五单元认识方程当中的《解方程(一)》为例,教学工作者在导入解方程这节课的时候,可以利用多媒体技术显示出天平的具象化图形,并让学生根据自身对于天平的理解,回答出天平的作用。教学工作者在教授的过程中,可以出示图1,并让学生根据图中的数字来表示平衡状态下苹果的质量。学生可能会根据图形表示出“10-2=8”的公式。教学工作者就可以在这个时候继续追问学生问题,比如“10-2和8的数字表示有什么意义呢?”学生在这个时候,就会明白天平是一种等臂杠杆,是一种衡量物体质量的设备。其作用是为了测量物体的质量和测量天平两端物体的质量是否等量。

图1
学生在认识了天平的作用之后,教学工作者就可以再次向学生进行提问:“如果把右边这个2g的砝码去掉,再放置一个纸质的空杯子,发现天平仍旧处在平衡的状态,那么就可以得出空杯子的质量为2g,但如果在这个时候往空杯子里添加一些水,天平又会发生怎样的变化呢?”学生就会对其回答“天平将会发生倾斜。”而此时再用公式表示天平两边的关系,就无法用等号连接。已知空杯子和苹果放在一起为10g,左边的砝码也为10g,而水的质量未知,学生要想表示天平右边的质量,就需要设置水的质量为x克,并把两者相加表示天平右边的质量,公式则表示为10+x。
此时,教学工作者可以继续借助多媒体技术显示出在天平左边添加10g砝码的图像,并让学生对图像进行观察,说出天平呈现出来的情况,并用公式表示出来。学生根据图像当中天平向右倾斜的状况分析得出“10+x>20”的公式,教学工作者就可以在这个时候显示出在天平左边又添加5g砝码的图像,让学生再次观察出天平呈现出来的情况,并用公式表达出来,学生根据天平的平衡状态判断出“10+x=25”的情况。
学生通过上述观察和分析,就可以认知到等量关系的具体含义。也明白只有天平保持平衡的时候,两边的物体质量才会呈现出相同的状态,且这时才能用等号去表示。学生能够通过这个过程,直观认知到方程模型,并初步了解未知量和已知量之间的关系。
2.归纳已学知识,建构完整知识体系
学生刚开始建构方程模型的时候,会通过观察、探究、概括和推断的思维活动,建构出一个不够具象化的方程模型。但经过对知识的概括和归纳,加之教学工作者的不断引导,学生能够给自己建构起一个完整的知识体系,学生可以在这个过程里提高自身的反思能力和探究能力以及归纳整理知识理论的能力。
以小学数学北师大版第五单元认识方程当中的《方程》为例,教学工作者在教授学生“方程的含义”时,就可以通过提问探究的方式,让学生逐步理解方程和等式之间的关系。教学工作者可以提出这样问题:“同学们,你们可以仔细观察一下黑板上所显示出的计算公式,你可以把它们进行分类吗?(“10+x=20”、“x+20<50”“20+30=50”“30+y>60”等计算公式)。”很多学生在看到这样的问题之后,都会根据符号的不同进行分类。而在此时,教学工作者就可以明确等式的含义。让学生知道左右两边数目相等的算式就是等式。
此时,教学工作者可以让学生再次观察等式的不同类型。学生就可以根据等式数字和符号的不同对其进行分类,不少学生都把未知数和已知数之间的等式进行了分类,并总结出了方程的含义,即“含有未知数的式子就是方程。”
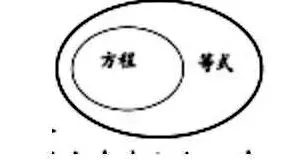
图2
为了让学生深入了解方程的含义,教学工作者可以通过多媒体出示出分辨哪些式子是方程的题型,比如:
判断以下哪些式子是方程?
X+2=6、30+60=90、20+x>60、y+60=200
学生可以根据等式的含义判断出X+2=6和y+60=200为方程。学生对于方程有了更深入的理解,教学工作者就可以引导学生对方程和等式之间的关系。学生这时候就可以在掌握等式含义和方程含义的基础上,对其进行剖析,学生能够通过自主推断的学习能力,发现等式和方程的关系就如图2的显示一般:等式包括方程,方程含于等式的关系。
3.运用方程模型,解决生活实际问题
从数学产生的历史过程就能够看出,数学起始于人们的劳动过程,人们想要解决生活中出现的一些问题,才发明了数字和公式。人们可以通过数学简单地处理生活中可能会发生的状况。教学工作者利用了天平的作用,让学生建构起了方程模型。教学工作者也可以在学生建构起方程模型之后,让学生运用方程模型对现实生活中出现的数学问题进行解答。而教学工作者在教授学生建立方程模型的时候,就需要设置一个与生活相关的问题情境,继而让学生通过方程模型解答问题,学生可以在这个过程中,直观地感受到方程模型的重要性,并形成“发现问题,建构方程模型,用方程模型解决问题。”的数学思维。
以小学数学北师大版第五单元认识方程当中的《解方程(二)》,为例,教学工作者可以在学生掌握了方程含义之后,提出生活化的数学问题,比如:
文文是xx小学的一名小学生,学校为了学生们的安全,购置了一辆送学生回家的校车。车载量为50人,在文文下车之前车上还有35个学生,那么在文文下车之后,车上还留有多少人呢?请用方程表示上述材料中的数量关系。
学生可以设置车上还有x个人,根据已知的量,可以用“50-x=36”的方程表示上述材料的关系。
还按照上述材料当中的人物和环境设置问题,假设文文知道车载量为50人,他和其他六个学生是第一批下车的学生,那么车上还有多少个人呢?并用方程表示上述材料中的数量关系、学生还是设置车上还有x个人,并根据已知的量,用“x+7=50”的方程表示上述材料当中的数量关系。
学生在解答完上述的情景问题之后,教学工作者可以让学生对“等号”所表示的含义进行解释。
教学工作者在此时就能够提出第二个生活情景式的问题,使学生根据不同的情景状况列方程。
情景一:已知一个公鸡重50克,而母鸡生下来的四只鸡仔加起来的体重和公鸡的体重相同,那么设置一只鸡仔的体重为y克。请你根据等量关系,列出方程。
情景二:已知一辆自行车用每个小时y千米的速度,行驶了4个小时,且一共行驶了50千米,请你根据等量关系,列出方程。
情景三:已知小明每天行走y千米,小红每天行走的量是小明的四倍,且总量为50千米,请你根据等量关系,列出方程。
学生掌握等量关系知识的基础上,列出了同样的方程,即“4y=50”的方程。教学工作者可以根据学生列出来的方程对其进行反问:“为什么三个场景完全不同,方程却呈现出相同的式子呢?”学生就可以通过乘法的运算法则来回答教学工作者所提出的问题。为了提高学生的反思能力,教学工作者可以让学生自主地设置一个符合“4y=50”的生活场景问题。学生在思考过后,就能够设置出这样的问题。
学生经过对等量关系知识的运用,解答出了运用方程表示校车人数数量关系的问题。而这个过程让学生既直观又具象化地看到了方程模式,并建立起了。而在第二个情景问题当中,教学工作者让学生通过相同的等量关系,表达出同一个方程。这样的题型可以让学生通过结构和知识的积累,认知到方程模式运用的规律。
结束语
综上所述,运用多样化教学方式帮助学生学习方程模型,有助于学生形成数学建模的思想。一旦数学建模思想形成,学生的学习效率就会有所提高。且对于培养学生的核心素养也起着相当重要的作用。教学工作者需要认清现如今的形势和学生的学习能力,并基于新课程改革的要求,在小学数学的课堂当中,培养学生构建方程模型的数学思维。这样才能够促进学生的综合能力得到进一步发展。

