大数据下的数学课堂研究
——以《锐角三角函数》复习课为例
丁 可
(南京理工大学附属中学 江苏 南京 210014)
1.案例背景
1.1 理论背景:《数学课程标准》指出:“要充分考虑信息技术对数学学习内容与方式的影响,开发并向学生提供丰富的学习资源,把现代信息技术作为学生学习数学和解决问题的有力工具,有效地改进教与学的方式。”随着南京市“网络与数字化环境下的教学实验项目”的启动,信息技术支持下的教学方法革新,已是如火如荼地走入教学实践。在初中数学的教学中,选用什么技术,如何设计数学教学环节是一个值得研究的课题。
1.2 实践背景:本案例的课题是:这个案例是基于笔者的教学实践,以初三一轮复习的第六章“锐角三角函数”为例,学生为本校初三(3)班的学生,学生已经有新授课的基础,对于锐角三角函数已经有了一定基础的学习,能够解决锐角三角函数这章的一些问题,但对于学生本章的掌握程度和未解决的问题,笔者没有充分的了解。针对中考复习的特点,课程教学的基本需求,借助数字化平台进行前测,通过即时数据让老师充分了解学情,分析出章节学习中没有完全解决的问题,把脉课堂,设计个性化学习路径。实现数据驱动下的ICT与数学学习的融合,进一步提升课堂效率。
2.案例描述
下面就这节复习课的片断进行分析,这节课的内容为《锐角三角函数》的复习课。
2.1 片段1:课前检测以了解学情,设计个性化学习路径。
笔者在课前通过数字化平台设计课前检测卷,课前检测共四题,涉及三角函数定义,特殊角三角函数,解直角三角形的应用三个方面的题目,通过数字平台的统计功能,发现学生三角函数概念题和特殊角三角函数题目做得很好,正确率较低的是应用题,有20人错误。
设计意图:《数学课程标准》指出:“教”与“学”是一件事情的两个侧面,其中“学“决定了“教”。作为教师,其角色是服务于学生,其作用是“根据教学需要组织教学”、“依据学生特点提供恰当的引导”。通过课前检测了解学情,从学生的实际问题出发,为设计适合本班学生学情的个性化学习任务单提供依据。
2.2 片段2:汇总问题,形成知识建构。
师:同学们,请同学们相互交流一下学习任务单上的基础训练部分的答案(课前五分钟已经完成基础训练),并思考本章你还有哪些疑惑的问题。(小组讨论)
师:大家基础训练有问题吗?(学生回答没有)那请同学们说说你觉得本章还有什么疑惑?
生1:老师,我对于这章的应用题感觉无从下手。
生2:应用题我不会列方程。
生3:应用题计算老是出错。
师:看来大家的问题都在应用题方面,本节课将重点复习应用题。
设计意图:课堂不应从常规的知识点进行全面复习。对于一些简单的知识点学生已经熟记于心,反复复习只会浪费宝贵的课堂时间。学生就任务单基础训练完成情况讨论交流,共同解决疑惑问题。笔者通过汇总学生的疑问,进一步了解的学生的薄弱方面,从而确立这节课的复习中心,让课堂更高效,更有针对性。
2.3 片段3:探究活动紧密联系,层层递进。
(1)合作探究,建立模型。
师:请同学们思考如何测量校园旗杆的高度,现在小丽和小强给出了两个测量方案,请同学们小组讨论这两个方案,合作求解旗杆AD的高度。(任务单上的题目如下)
问题:如何测量校园旗杆的高度?
为了测量校园内旗杆的高度,小丽、小强有如下的测量方案:
方案一:小丽在地面上的点B处观测旗杆AD的顶部,测得仰角∠ABC=β,然后他向旗杆前进了a米到达C处(如图所示)且B、C、D在一条直线上,此时观察旗杆顶部,测得仰角∠ACD=α,请根据小丽的方案计算旗杆AD的高度。
方案二:小强在地面上的点C处观测旗杆AD的顶部,测得仰角∠ACD=α,然后他向旗杆前进a米到达点B(如图所示),观察旗杆顶部,测得仰角∠ABD=β,此时B、C、D在同一直线上,请根据小强的方案计算旗杆AD的高度。
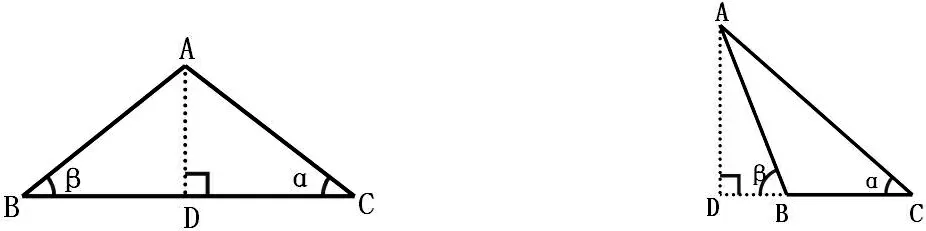
方案一如图 方案二如图
学生展开了热烈的讨论,然后独立完成求解。笔者巡视,并做个别指导。五分钟后,同学们完成了问题的解决,笔者在黑板上画出这两个图形。
师:同学们,这两个图形中各有几个直角三角形?
生:两个。
师:这两个直角三角形有共同的边吗?
生:有,是AD。
师:这两个直角三角形分别位于公共边的哪边?
生:异侧和同侧。
师:我们把这两种情况称为模型一与模型二。
(2)寻找模型,解决问题
师:我们应用题里面很多都可以归为这两种模型。请同学们小组交流一下下面的题目中有没有模型?如果有,分别属于哪个模型?(学习任务单上的题目如下)
我们一起找一找:
练习1:如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角是45°,楼底D的俯角是30°,楼CD高36米,求两座楼房的楼间距.
练习2:如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角是30°,在楼AB的楼底B点测得楼CD的楼顶C的仰角是45°,楼AB高36米,求楼CD的高度.
练习3:如图,楼CD高是2m,在DB上选取观测点E、F,从E测得楼CD和楼AB的顶部C、A的仰角分别为58°、45°,从F测得C、A的仰角分别为22°、70°.求楼AB的高度.
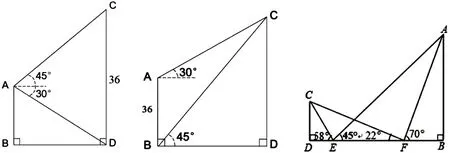
练习1如图 练习2如图 练习3如图
学生对于练习2的回答让笔者印象深刻。
生1:过C点做BA的垂线段,交BA延长线于E点,就出现了模型二。
师:那设什么为x呢?
生1:设CE长为x。
生2:过B点做BF∥AC,交CD于F点,就有模型二了。
师:非常棒。还有其他方法吗?
生3:延长CA与DB交于G点,这样就也有模型二了。(下图)
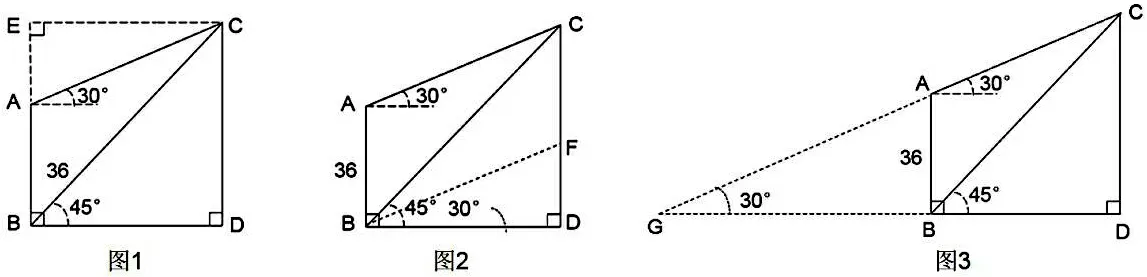
笔者正准备表扬这三位同学,教室瞬间掌声雷动,同学们都投来了赞许的目光。
师:同学们都回答得非常好,看来对于模型的运用还是不错的。下面我们看练习3,谁来说说看,这道题目中有没有模型?小组讨论起来。
各小组热烈地讨论,不一小会儿,就有很多同学举起了小手,看来都找到了解决方案。
生4:这边有两个模型,左边和右边各有一个,都是模型二。先通过左边的模型求出EF的长度,再用右边的模型求出AB。
师:回答得太棒了,请同学们根据这个思路完成本题的解答。
设计意图:通过“合作探究,建立模型——寻找模型,解决问题”的流程使学生经历知识发生、形成和应用的过程。模型的建立来源于生活实际,以贴近学生生活的测量校园旗杆高度出发,模型为解决实际问题而产生。模型的建立终归是为了再次解决其他实际问题,所以“我们一起找一找”环节又将模型应用于实际问题,符合数学知识来源于生活,又应用于生活的学科定位。加深学生对于本章应用问题的理解,会准确地抽象出模型,从而解决实际问题。
2.4 片段4:课堂检测,链接中考。在课堂针对性的复习后,笔者想了解学生的课堂学习效果,为后续的教学做好准备。笔者利用数学平台组卷,但发现平台上现成的题目有限,并且想用一道近几年的中考题,通过与平台工作人员沟通,将需要的题目编进了题库,使用起来更便捷,更灵活。并且考虑到课堂剩余时间有可能不够,课堂检测为一道应用题。(课堂检测题目如下图)课堂检测:

课堂检测的正确率达到84%,总体完成非常得好,这也印证了本节课的课堂效果较好。
设计意图:《数学课程标准》中指出:“新课程理念下的数学学习评价应做到:要能对考试结果进行科学的分析和总结,根据考试的结论及时改进教学工作。”在数字化平台上进行课堂检测,平台能够及时地反馈数据,便于教师分析数据,更高效地把控课堂。
3.案例反思
这节课对笔者的震撼比较大,我们以前习惯了教师根据自己的分析设计课堂内容,这往往与学生的实际情况相差太远,从而导致学生会的知识点反复讲,不会的知识点讲不透。在这次实践中,学生不再是课堂的被动接受者,而是拥有了课堂的决定权。“以学定教”大大扩充了课堂容量,在课堂有限的时间中深化学生对于未知知识的探索。并且数据驱动下的ICT与数学学习的融合,进一步提升了课堂效率。下面就本节课“以学定教”的实践活动,与大家分享一下我的几点感触:
3.1 “以学定教”应根据学生的实际学情决定课堂内容和形式。要提高课堂效率就要改进课堂形式和课堂内容,以往我们的中考一轮复习总是面面俱到,教师恨不得把学过的知识全部再讲一遍,总觉得学生遗忘了,又不会了,教师有千万个不放心。导致课堂重复讲解,需要深化的知识没有时间讲,简单的题目重复练习,这样的结果是:教师很累,学生厌烦,复习效果大打折扣。通过这节课笔者更加体会到:课前必须根据学生的学情设计学习任务单,课堂重点应放在学生掌握得不好的知识,基础知识和已经掌握的知识只需基础训练以达到熟练的目的,这个可以放在课前进行。学情通过两方面进行了解:课前检测题与学生反馈汇总。两方面结合全面了解学生学情,这是课堂设计的决定要素。本节课是处在中考一轮复习,学生已经有了一定的基础,但对于本章学生的薄弱点并不十分了解,课前检测题共四题,分别涉及三角函数定义、特殊角三角函数、直角三角形的简单应用和实际应用,涵盖了本章的所有考点,能够全面了解学生的新课掌握情况。题目难度适中,能够较好地反映所在问题,平台的参与方便快捷地提供数据,为教师的教学减轻了负担。
3.2 “以学定教”应合理设计学习任务单,突出重点,攻克难点。学习任务单包含了三方面内容:一是知识梳理,二是基础训练,三是解决问题。第一项和第二项在课前完成,不占用课堂时间,起到梳理知识点和训练基础题的作用。本节课的重心在于第三点攻克应用题难关。在课前了解了学生的盲点在应用题后,笔者对于应用题进行了深入的研究,发现80%的应用题都和两个模型有关,而提高学生应用题的正确率,必须完善学生对于模型的认识,从而确定了本节课解决问题的开始从两个模型的生成入手。在学生对于模型有了一定的认识后,又设计了三道应用题,让学生从中找模型,加深对于锐角三角函数应用问题的理解,同时通过寻找模型了解学生对于模型的认识是否到位,从而达到本节课的目的——攻克锐角三角函数的应用题这一难点。
3.3 “课堂检测”为下节课的“以学定教”设计课堂提供依据。“课堂检测”不仅能检验这节课的教学效果,也决定了下节课的复习内容,是否需要进一步复习锐角三角函数的应用。本节课的课堂检测正确率达到84%,可见学生的正确率较高,笔者认为锐角三角函数应用题难点被攻克,后面相应地设计一些应用题训练,学生在这类应用题上应该会做得比较好。并且现在数字化平台发展迅猛,众多的平台看中教师的体验感受,并能及时给予技术支持和平台优化,这为“以学定教”设计课堂提供了优质保障。
如何更好地利用好数字化平台,实现“以学定教”,准确把握学情,合理设计出满足学生需求的数学课堂,对于其中的有些问题我们还无法给出令人满意的答案,但笔者希望这些问题能成为进一步研究的起点,触发大家去反思、去研究,通过不断实践,我们一起去寻找一条适合当代中国学生实际情况的有效途径。

