深度探究问题，发展运算素养*——以一道圆锥曲线压轴题为例

于 洋

(江苏省南京师范大学附属中学 江苏省南京市刘明名师工作室 210003)

高中数学离不开数学运算，在《普通高中数学课程标准(2017年版)》中，数学运算素养被定义为高中数学六大核心素养之一．在高中数学的教学实践中，一线教师普遍发现学生在运算思路的探索和运算程序的设计上存在不足和欠缺[1]，然而运算思路的产生是解决数学问题的关键，运算思路是在深入分析运算对象、结合运算对象灵活使用运算法则的基础上产生的，是体现数学运算素养的精华[2]．因此，提升学生寻找运算思路的能力将有助于提升学生的数学运算素养．本文通过对一道圆锥曲线压轴题的多角度探究，启发学生思考运算方向，助力学生发展数学运算素养．

1 问题呈现

(1)求椭圆的标准方程；

(2)设P(0,1)，点A，B为椭圆的左右顶点，过A作斜率为k1的直线交椭圆于E，连结EP并延长交椭圆于F，记直线BF的斜率为k2，若k1=3k2，求直线EF的方程．

2 解法探究

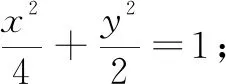
思路1 借助求根，关注通法

评注许多同学面对②式束手无策，因为由韦达定理得到x1+x2，x1x2无法直接代入②式．这里运用求根公式破解上述问题，无论x1和x2的系数是多少都不会影响到求根公式的代入.可见求根公式是解决解析几何问题的通性通法，虽然繁琐但有时能起奇效，要引起教师的足够重视．

思路2 局部化简，优化运算

思路3 联系和积，逐步求解

思路4 运用结论，构造对称

即6(kx1+1)(kx2+1)=-(x1-2)(x2-2)．化简得(6k2+1)x1x2+(6k-2)(x1+x2)+10=0．

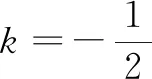
思路5 曲线消元，突破定势

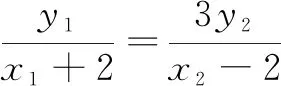
思路6 齐头并进，一算到底

3 聚焦解题方法，提炼运算本质

在数学课堂上，六种解法一一展现，学生们听得如痴如醉，积累了解决复杂解析几何问题的经验，拓宽了解决数学问题的方法，但是看似精彩的课堂又能使学生收获多少呢？已有的研究表明：教师在一题多解教学中常常盲目地追求解法的多样，忽视解法优劣的比较，导致学生把几种解法放在同等的地位，下次面对问题时依然束手无策，“会解”与解决问题之间还存在着真实的差距[4]．所以，根据已有的研究成果[5]，笔者采用思维导图(图1)，启发学生对解决问题的六种路径进行全景式呈现，对解题思维进行精细化剖析．

图1

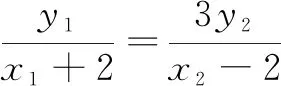
进而得到结果．通过深入分析，我们进一步发现解法一、二、四、五的本质都是将问题转化成为关于k的一元方程，虽然这四种解法看似令人眼花缭乱，但究其本质其实是消元思想的实际应用．解法六与前面五种解法的区别在于利用y=k1(x+2)和y=k2(x-2)分别与椭圆方程进行联立，利用k1=3k2化简得到关于k1的一元方程再求解k．解法六运算繁琐背后真正的原因在于不是将解题的目标定位于求解k，而是借助k1求解k，本题k1的求解异常复杂导致学生利用解法六功亏一篑．通过不同方法之间的比较，学生进一步理解了各方法的原理，理清了不同方法运算优劣的原因，领会了消元思想在运算方法上的“高屋建瓴”．

4 反思探究过程，提升运算素养

(1)重视通性通法，打牢运算基础

现在的解析几何教学，一遇到复杂的数学运算时，有的教师就引导学生选取更简便的运算途径，但是简捷的运算方法往往“技巧味”浓，学生短时间内难以掌握导致考试时依然不会做．有的教师过度重视数学运算的技巧导致学生忽视了数学运算中的通性通法，就像解法1中，化简到2kx1x2+(2k+3)x1+(6k-1)x2+8=0这一步，就启发学生思考其他方法而不是对这个问题进行深入探究，也没有充分引导学生利用已有的知识去尝试解决问题，从而导致学生失去了一次训练运算基本功的契机，失去了一次成功解决问题的体验，更失去了一次提升运算素养的机会．长此以往，学生看到复杂的式子就产生了畏难情绪，不敢动笔，其数学运算素养就难以提高．因此，笔者在课堂上给予学生充分的思考时间，利用小组讨论，启发学生不断思考解法1“能不能走下去”，最终得到求根公式的方法，使其恍然大悟，原来解决这个问题的方法在初中就学习过，这就促使学生掌握解决解析几何问题的基本方法．在课堂上，教师要引导学生敢于进行复杂计算，加强对具体运算过程的示范、引领、指导和要求，在练好数学运算基本功的基础上再寻求简捷的运算方法[6]．

(2)顺应思维发展，突破运算障碍

(3)发展多元思维，优化运算水平

通过这道圆锥曲线的多角度探究，启发学生发散思考，通过解法1和解法2，在求根公式的基础上局部化简，帮助学生掌握解析几何运算中的通性通法．通过解法3，启发学生用数学的眼光观察世界，从联系的视角探究运算对象之间的关系，发现韦达定理中和与积的关系，从而化积为和，找到问题解决的方向．通过解法4和解法5，引导学生借助解析几何二级结论和曲线方程本身将问题中的非对称结构转化为对称结构，从而实现韦达定理的顺利代入，拓宽学生解决问题的视野，深化“消元”思想的理解．通过解法6，让学生经历复杂的运算，探究繁琐运算背后的成因，使其感悟到：围绕数学问题对象直接运算是简化运算的关键．最后，笔者借助思维导图促进学生对问题结构与方法的比较，突出方法的本质，不断优化解决问题的路径，从而促进学生选择解决问题的最优方法，实现解题最大效能．