借助思维可视导引 优化高三复习效果*

陆 丽

(江苏省太仓高级中学 215411)

数学是理性的，而学生的数学思维是隐性的、不可视的.因此，教师要在充分了解学生的思维情况的基础上组织教学.思维可视导引教学，就是以图示或图示组合的方式，将抽象的数学研究对象变得可视，让学生在基本活动经验聚集的过程中打开思维的大门，让内隐的数学思维展露出来.它有利于教师有效引导，可促进课堂教学的高效开展，实现数学知识、方法、思想的主动建构，优化学生的思维品质.它不仅是一种教学策略与方法，更是一种教学思想与观念.本文以高三微专题复习课“与三角函数有关的导数问题”为例说明如何借助思维可视导引，优化高三复习的效果.

1 导图探路，明晰思维方向

在高三教学中，教师要认真研读课标，研究高考评价体系，使学生深刻领悟“为什么学”(高考要求)、精准聚焦“学什么”(要解决的问题)、具体实现“怎么学”(需要经历怎样的历程，如何达到).如果能将教学目标、教学重点及难点有效融入到思维导图中，借助思维导图让学生明晰思维方向，这将大大促进学生提升学习意识和思维能力.

教学片段1呈现表1，指出与三角函数有关的导数综合问题是近几年高考命题的一个重要方向.观察这些考题，从函数解析式的形式看，它们是三角函数与多项式函数、分式函数、指数函数与对数函数叠加的复杂函数；从研究问题的类型看，它们涉及到考查函数的单调性、最值、极值、零点及不等式恒成立等问题，其本质就是研究这些复杂函数的性质.最终教师给出思维导图(图1)，指出本节课的教学目标：如何研究这些与三角函数有关的复杂函数的性质，有哪些方法.

表1

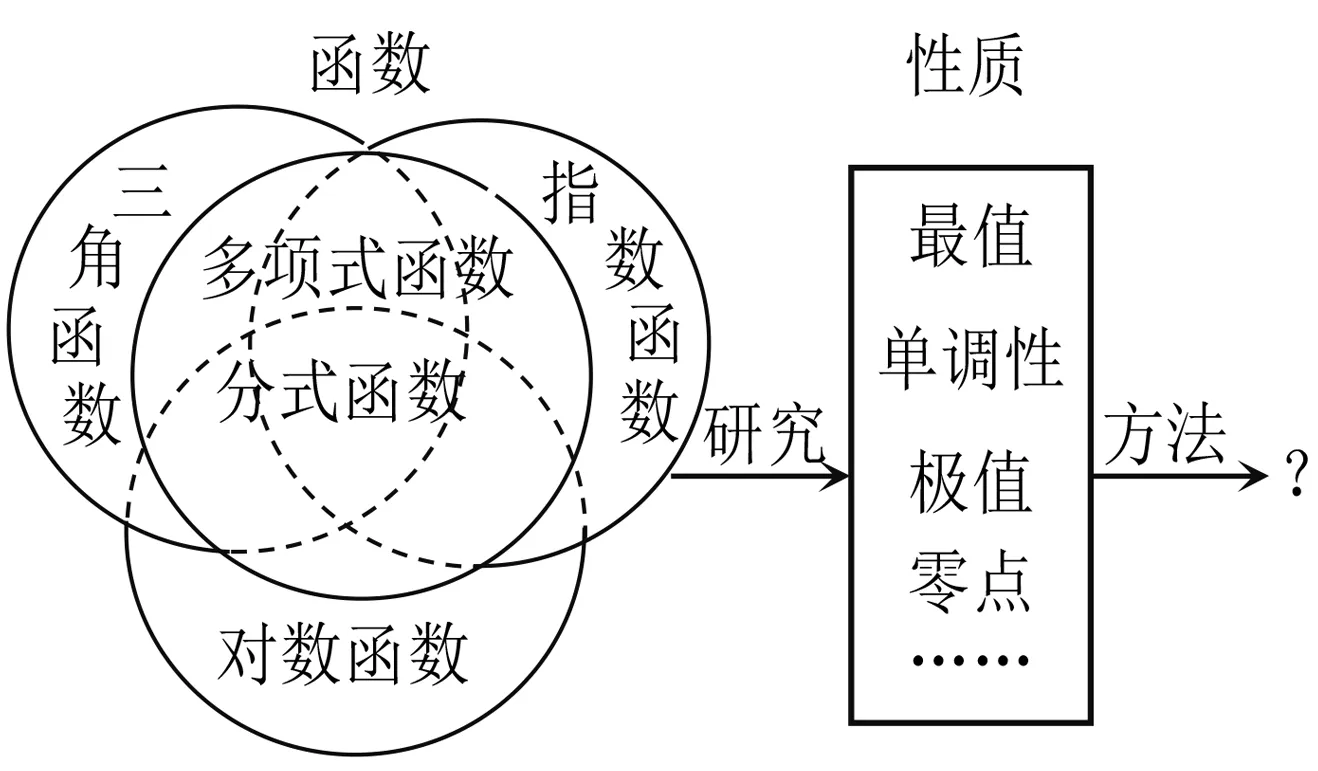
图1

本片段看似简单，实则起到了对本节课核心问题的定位作用，能激发学生应用所学知识、方法解决相关问题.同时，借助思维导图，让课堂目标清晰可视，为学生提供了可视化的思维路径，便于学生有序开展研究.

2 探究留痕，呈现思维轨迹

课堂上学生的参与不仅是行为上的参与，更是思维上的参与.教师要尝试通过各种方式激活学生的思维，培养学生的思维品质.在高三教学中，数学思维伴随数学解题探究的全过程，这些内容如果仅凭有限的记忆是不够的，更需要我们将题目的条件、目标、解题思路、各解题方法的适用条件及可能遇到的困难，甚至一些转瞬即逝的想法清晰地记录下来，留下思维轨迹，便于学生认识数学知识的本质，更能认识数学方法之间的关联，从而优化解题策略.

教学片段2教师给出以下四个热身练习题：

1．(2018全国卷I理第16题)已知函数f(x)=2sinx+sin 2x，则f(x)的最小值是．

2．函数f(x)=x2-4xsinx-4cosx在 (-π,π)上的零点个数是( ).

A.1 B.2 C.3 D.4

3．若关于x的不等式ex+cosx≥a+2在 [0,+∞)上恒成立，则实数a的最大值是( ).

A.0 B.1 C.2 D.3

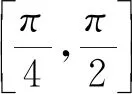
在高三复习中，很多学生喜欢总结出一定的解题模式，然后机械地套用固定模式解题，这样学生的思维容易固化，形成一定的思维定势，不利于发展创新思维．很多学生在遇到与三角函数有关的导数问题时，都不假思索地进行求导研究，一次求导不行，再二次求导，甚至三次求导．针对这样的固化思维，教师设计了热身练习1和2，旨在让学生能够借助函数式的特征分析，如函数的性质(奇偶性、周期性)简化研究对象，从而将整体问题转化为局部问题，再借助导数工具研究局部问题．

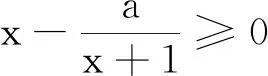
在每个热身练习探究的过程中，教师及时将问题、思路、方法、技巧等一点点地记录下来，思维的路径抽丝剥茧般地在图示上一步步呈现出来，形成了下面的思维轨迹图，这就使学生学习有迹可循，使其中蕴含的数学规律自然地“浮出水面”，形成方法体系．

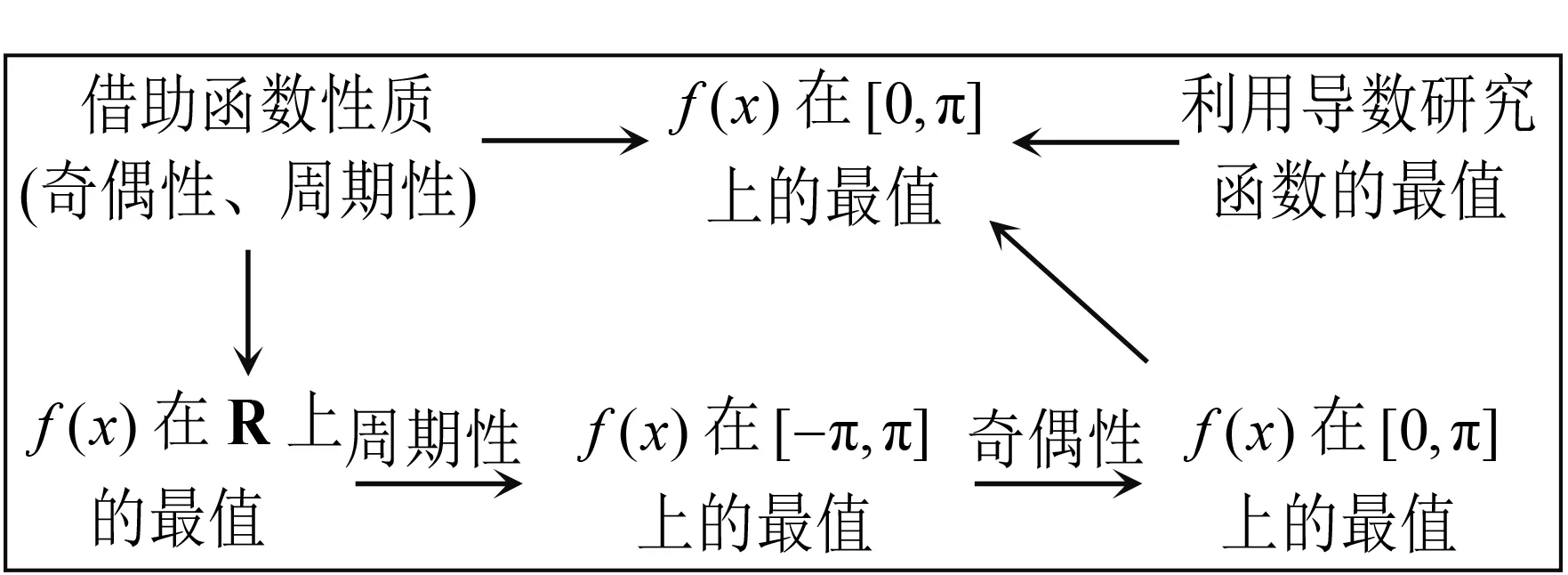
图2 热身练习1思维轨迹

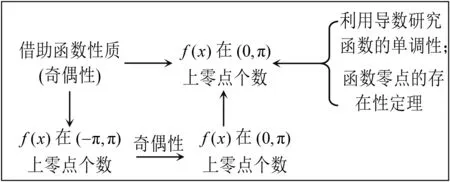
图3 热身练习2思维轨迹

图4 热身练习3思维轨迹

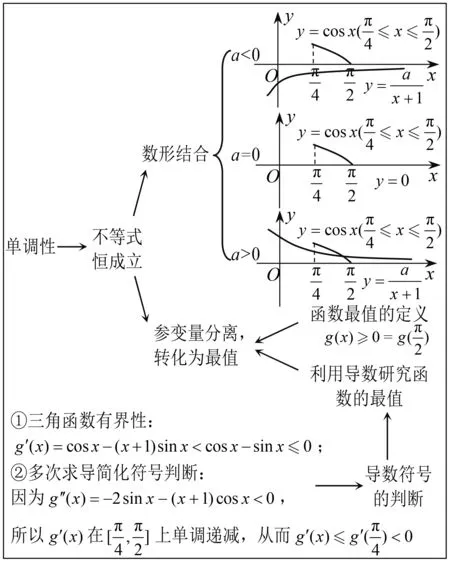
图5 热身练习4思维轨迹

3 多维表达，物化思维成果

让思维可视，需要调动学生的多种器官参与课堂活动，将课堂中的探究发现运用数、形、结构等多种数学表征方式表达出来，物化思维成果．

教学片段3教师给出以下例题：

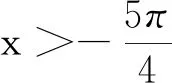
方法1：从数的角度表征

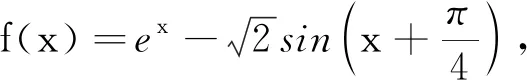
方法2：从形的角度表征

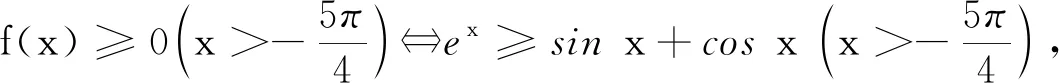
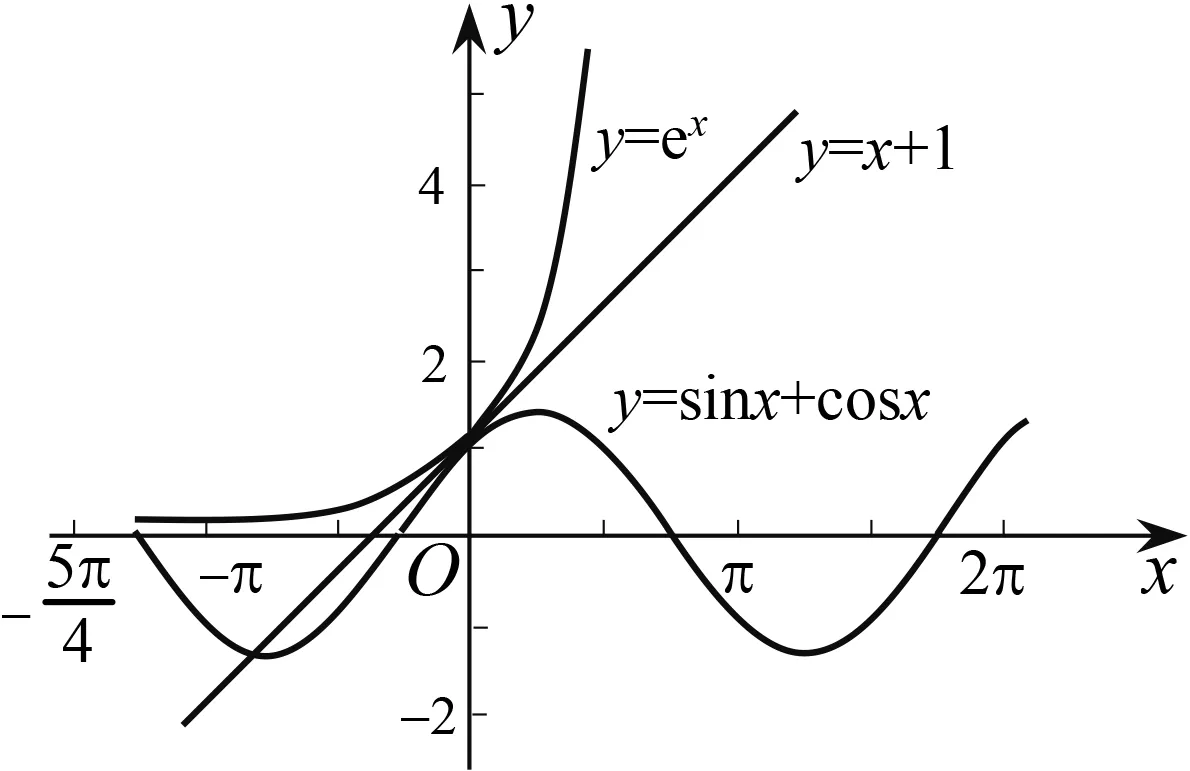
图6

方法3：从结构角度表征

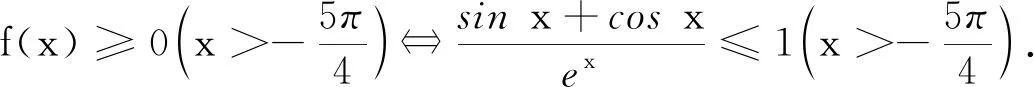
4 整体感悟，形成思维结构

研究表明，学生的思维都是从点状阶段逐步向线状、网状、结构状阶段发展．因此，在高三教学中，教师要想尽办法拓宽思维空间，对学生孤立的、碎片的、零散的思维经验进行整体的梳理、完善、建构，使知识、方法、思想不再是杂乱无章的堆积，而是有秩序、有层次、有系统的“串联”，使学生形成结构化的思维，切实提高高三复习效果．

教学片段4问题：本节课你收获了哪些基本知识？哪些基本技能？哪些基本思想？哪些基本活动经验？

学生畅所欲言，教师逐层显现思维结构图(图7)，使学生在大脑中建立起函数导数章节的体系，明确如何研究与三角函数有关的复杂函数的性质、在什么条件下直接研究函数的特征、在什么条件下用导数研究函数性质、如何用、有哪些主要的解题技巧、又蕴含着哪些思想，等等.通过学生基本活动经验的汇集、思维结构图的梳理，使学生能够把“四基”内化于心，能够做一题会一类通一片，逐步形成一种意识、观念和素养，运用到后续的学习中去．

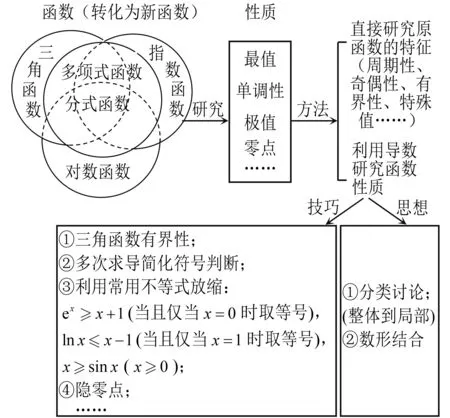
图7

美国图论专家哈里说：“千言万语不及一张图.”借助思维可视导引教学，可以让隐性的思维变外化显现、抽象的思维变形象可视、零散的思维变整体有结构.教师能更准确地把握学生思维的走向和水平，能让学生认识数学知识的本质，理清数学方法之间的逻辑关联，促进学生深度思考，不断提升学生的学习力，更好地促进学生数学核心素养的形成.