一道高二数学期末统考题的解法探究与拓展

张海泉

(江苏省兴化中学 225700)

本文先对2021年泰州三市三区高二数学期末统考的一道试题的解法作些探究，再将试题进行纵向、横向推广与延拓，形成一般问题的解题思路,以期达到举一反三、触类旁通的教学效果.

1 试题呈现

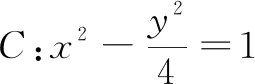
图1

2 解法探究

3 解后反思

本题是一道圆锥曲线中的定值问题，题目设计入口较宽，学生容易想到联立直线与双曲线方程求出两直线交点，转化为非对称的韦达定理形式求解.题目设计的直线过焦点，所得交点P恰好在双曲线的准线上，很好地展示了双曲线的一个完美特殊性质，故学生易产生疑问：如果直线不是过焦点,是否也有类似的性质呢？

于是课堂上试着将题目变为拓展题供学生探究.

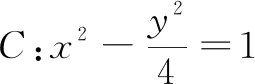
4 猜想探索

5 归纳模型

基于学生的这种发现，试着从一般形式来探索.

探索过程：

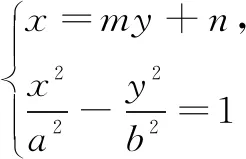
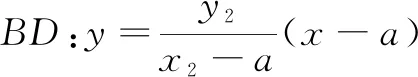
6 拓展延伸

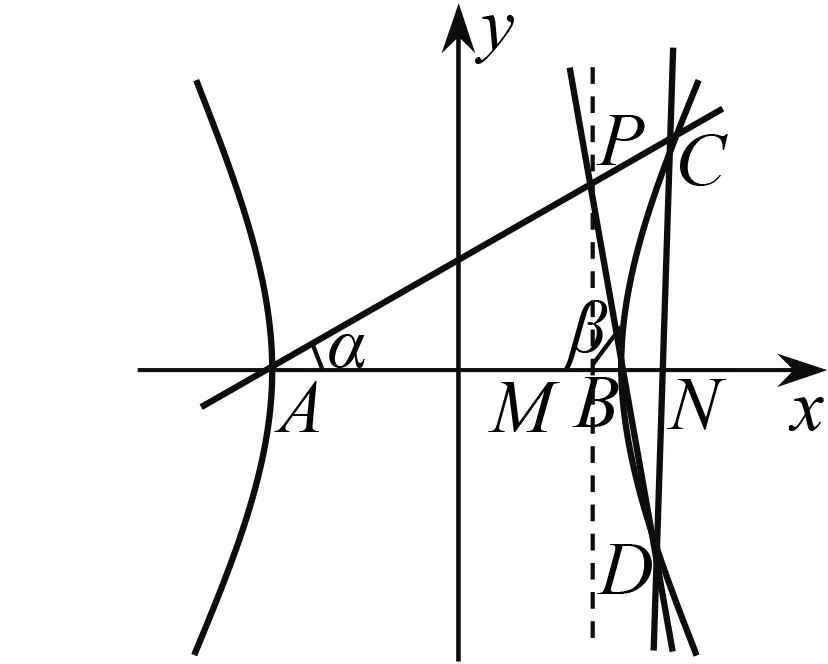
图2

这样，从教师的命题角度来看，本题可以以点带面扩大试题的教学功能.于是进一步将定点拓展为定值问题.

7 纵向探究

所以D，N，C三点共线，即直线CD过定点N(n,0).

8 横向探究

由于椭圆和双曲线有统一定义，因此本题的探究过程可以类比到椭圆中，扩展出椭圆中的一般结论(留给读者自行探究).

要给学生一杯水，教师就要有一桶水，且须是一桶新鲜活水.因此，讲授一道题，教师不能向学生一样仅仅满足于会解题，还需要考虑如何高效解题，注重通性通法，拓展探究、挖掘试题的内涵和外延，找到试题的源头，研究出一类题的解题规律，形成一种思维上的升华和命题模板，达到放得开、收得拢的自如境界.