数据分析观念下新高考“概率与统计”试题特征及启示——以2020年和2021年新高考全国卷为例

叶立军 赵亚婷

(杭州师范大学经亨颐教育学院 311121)

1 问题提出

“概率与统计”是高中数学课程内容的重要组成部分，在整个高中数学课程中占有中心地位．同时，数据分析是概率与统计教学的核心，概率与统计是学生数据分析素养发展的知识载体．[1]以下以2020年和2021年新高考全国Ⅰ卷、Ⅱ卷为例，从宏观与微观两个维度研究新高考全国卷概率与统计试题的命题特征，对统计与概率的课堂教学提出建议，提高学生数据分析素养．

2 概率与统计试题内涵及特征

当前对概率与统计试题的概念没有统一界定，本文中我们根据考查知识点的内容将概率与统计试题内涵界定为“考查内容为概率与统计相关知识点的试题”．

概率与统计试题具有如下特征：

(1)应用性

概率与统计试题作为数学学科与生产生活实际联系的主要渠道[2]，在现实生活中的应用极为广泛，呈现生产、生活、科研等不同领域的应用需求，其分析结果用于解决现实问题，体现较强的应用性．

(2)情境性

情境是高考实现价值引领、素养导向综合考查的载体．[3]概率与统计试题均设计了具有鲜明时代特色、新颖且真实的情境，考查学生在熟悉或陌生情境下利用概率统计知识解决实际问题的能力，体现较强的情境性．

(3)综合性

概率与统计试题通过构建真实的情境将数学各个知识点串联加以贯通考查，如在试题中除了考查概率统计之外，还考查函数、数列等内容．同时，概率与统计试题也关注综合核心素养的考查，在关注数据分析素养的同时也关注逻辑推理、数学运算等素养．

3 概率与统计试题分析

3.1 分析框架

依据概率与统计试题的内涵与特征，从宏观与微观两个方面分析新高考全国卷中的相关试题，如表1．

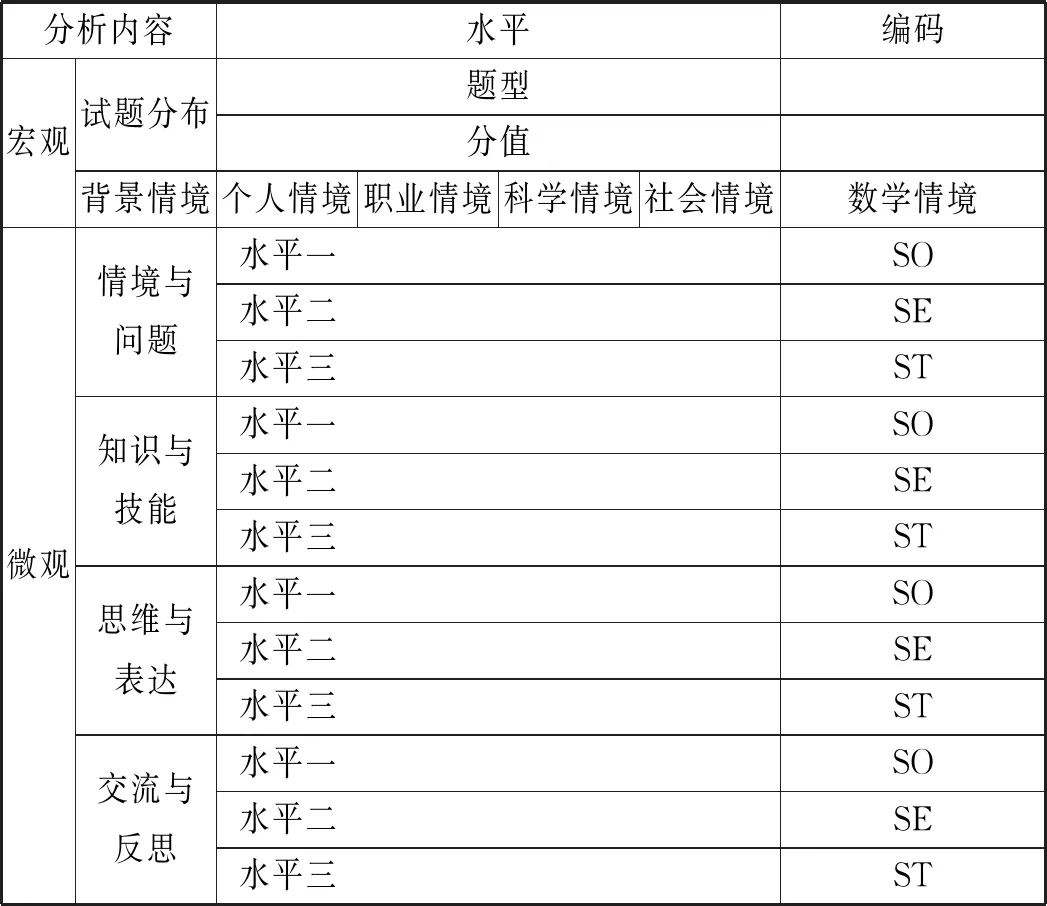
表1 分析框架

宏观方面为概率与统计试题的分布情况以及根据PISA2021的分类对试题的背景情境进行分析．其中，把PISA2021中的科学情境分离出纯数学情境．

微观方面借鉴高中数学课程标准对核心素养划分的四个维度、三个水平进行分析．

3.2 宏观分析

(1)试题分布分析

统计2020年与2021年新高考全国卷概率与统计试题的题型、分值和总分情况，如表2．

表2 概率与统计试题的分布情况

由表2，新高考全国卷分为Ⅰ、Ⅱ卷，从试题类型上看，新高考全国卷概率与统计试题分布在选择与解答这两个部分，基本上是以一道单选题(5分)、一道多选题(5分)、一道解答题(12分)，总分22分的固定模式进行考查．

(2)背景情境分析

依据改变后的PISA2021对概率与统计试题进行分析，如表3．

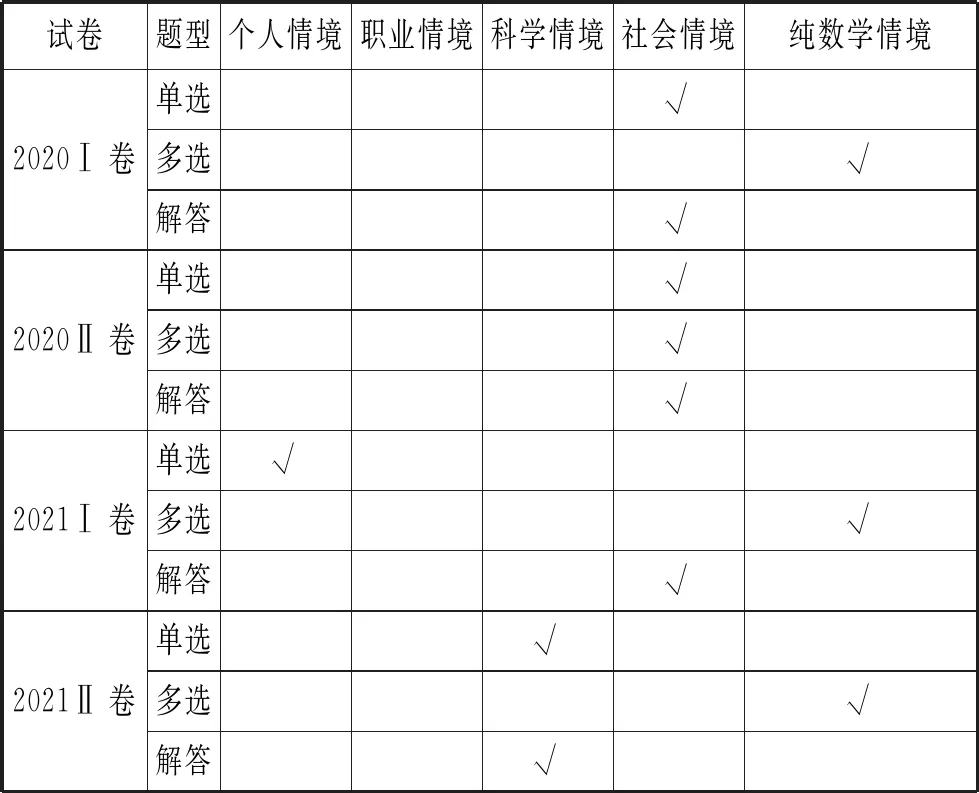
表3 概率与统计试题情境分析表

由表3，2020年新高考全国卷概率与统计试题倾向于借助社会背景来考查学生对知识的掌握，其他背景情境比较欠缺．而2021年新高考全国卷概率与统计试题的背景情境类型较丰富，不仅仅局限于社会情境．2021年新高考全国卷概率与统计试题在关注社会现象的同时也在关注试题与生活的联系、跨学科的应用．

3.3 微观分析

按数据分析素养四个维度进行分析，如表4．

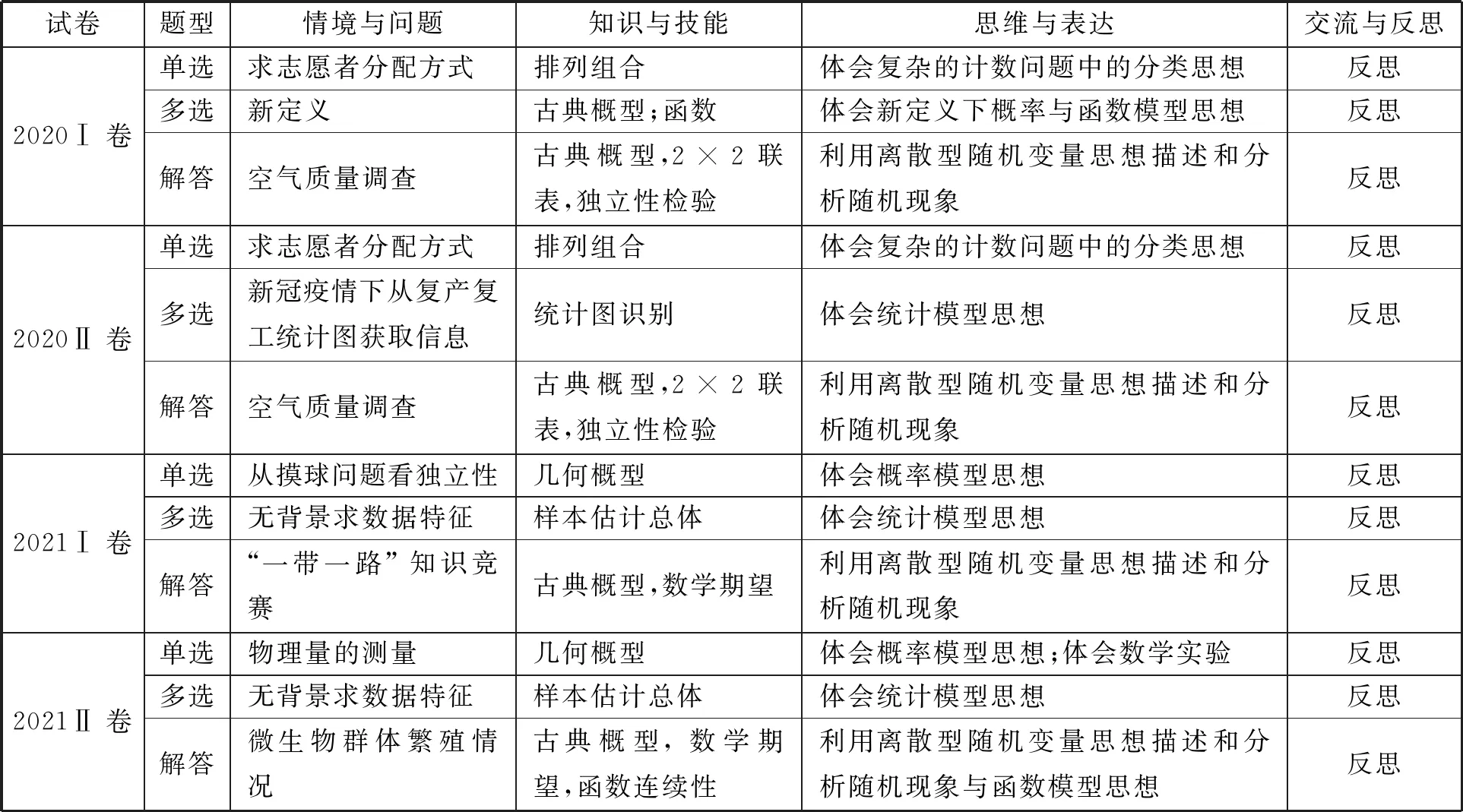
表4 概率与统计试题四个维度考查情况

由表4，在情境与问题方面，新高考全国卷均从熟悉的情境来设计数学问题．同时，2021Ⅰ卷以“一带一路”为背景进行考查，结合时政、关注社会发展．在知识与技能方面，试题主要考查统计图识别、几何概型、古典概型与排列组合，或附加考查函数的内容，关注知识的整合．在思维与表达方面，主要要求学生在一定程度上可以利用离散型随机变量思想去描述和分析随机现象，也关注学生可以用统计或概率模型表达随机现象，体会统计和概率的模型思想．在交流与反思方面，按照“反思”的含义，学生在做题时也有“反思”的过程[4]，比如检查计算的结果等．

对概率与统计选择题部分按数据分析素养三个水平进行分析，如表5．

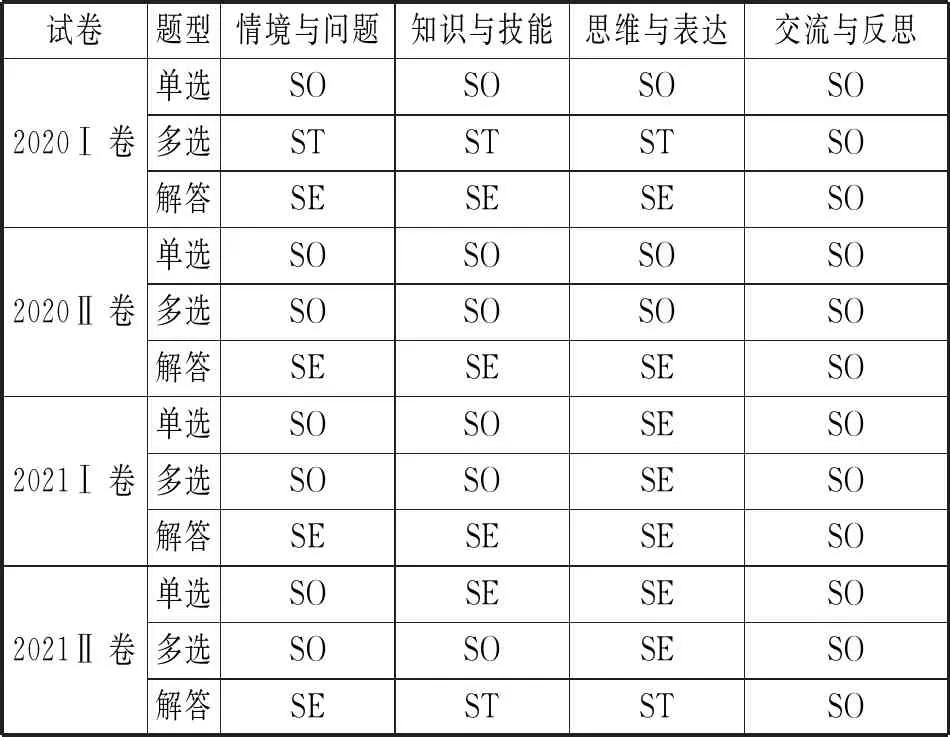
表5 概率与统计试题三个水平考查情况

由表5，新高考全国卷中概率与统计试题选择题部分集中考查水平一和水平二，对水平三的考查较少．其中，在2020Ⅰ卷中出现利用概率部分知识考查新定义试题，在核心素养的四个维度中考查水平较高．而解答题部分在核心素养的四个维度除了交流与反思外，其余水平均达到水平二，并且2021Ⅱ卷的解答题在知识与技能、思维与表达方面均达到水平三．新高考全国卷均在关联的情境中，对学生能否针对具体问题，运用适当的统计或概率模型解决问题，用统计或概率模型表达随机现象的统计规律进行考查．

为了解新高考全国卷在核心素养的四个维度考查哪个水平为主，绘制数据分析素养的三个水平百分比堆积图，得图1．

图1

由图1，数据分析素养集中考查水平一和水平二，对高水平素养考查较少．可见数据分析素养的考查比较重视基础，以知识的理解和迁移为主，较少考查知识创新．

4 试题命题特征

4.1 试题立意高、起点低，注重对数据分析素养的考查

新课标要求在概率与统计方面注重基本概念的理解，着眼于知识在理解基础上的应用．[5]新高考全国卷概率与统计试题体现课标要求，注重学生在解决问题的同时培养数据分析素养，但试题起点较低，考查均为常规的、熟悉的知识内容，考查水平集中在水平一和水平二．

例1(2020Ⅰ卷第3题)6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去一个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有( )．

A．120种 B．90种 C．60种 D．30种

例2(2020Ⅰ卷第6题)安排3名学生到2个乡村做志愿者，每名学生只能选择去一个村，每个村里至少有一名志愿者，则不同的安排方法共有( )．

A．2种 B．3种 C．6种 D．8种

例3(2021Ⅰ卷第8题)有6个相同的球，分别标有数字1, 2, 3, 4, 5, 6，从中有放回地随机取两次，每次取1个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则( ).

A．甲与丙相互独立 B．甲与丁相互独立

C．乙与丙相互独立 D．丙与丁相互独立

例1和例2考查的知识点是基础的分步乘法计数原理，体会统计的模型思想．例3的知识点是事件的相互独立性，体会概率的模型思想．这三题均是对数据分析水平一的考查，要求学生能够面对熟悉的情境选择合适的统计概率模型来解决问题，关注学生数据分析素养．此类题以单选题为主，考查难度不高．

4.2 试题体现综合性，注重考查综合应用能力

新高考全国卷试题具有较强的综合性，注重知识点的整合和运用．具体表现为注重在知识的交汇处设计试题，从不同的角度分析数据，综合考查不同的数学学科核心素养[6]．如将统计与概率加以整合，或将概率统计与函数、数列等加以结合设计问题，考查学生综合运用知识的能力．

例4(2021Ⅱ卷第21题)一种生物群可以经过自身繁殖不断生存下来，设一个这种生物为第0代，经过一次繁殖后为第1代，再经过一次繁殖后为第2代……，该微生物每代繁殖的个数是相互独立的且有相同的分布列，设X表示1个生物个体繁殖下一代的个数P(X=i) =pi(i= 0, 1, 2, 3)．

(1)已知p0= 0.4，p1= 0.3，p2= 0.2，p3= 0.1，求E(X)；

(2)设P表示该种微生物经过多代繁殖后临近灭绝的概率，p是关于x的方程p0+p1x+p2x2+p3x3=x的一个最小正实根，求证：当E(X)≤1时，p=l，当E(X) > 1时，P< 1；

(3)根据你的理解说明(2)问结论的实际含义．

例4把概率的相关知识和函数与导数结合出题，是对数据分析素养的考查也是对逻辑推理素养的考查．该试题具有较强的综合性，要求学生对相关知识熟练掌握．

4.3 情境蕴含时代气息，体现统计的教育价值

时政和社会热点话题作为数学问题的背景出现，在考查学生数学理解能力的同时，也在引导学生关注国家发展．[7]新高考概率与统计试题以我国时政为背景情境，强调我国近几年的发展，树立学生“四个自信”，潜移默化影响学生的价值观．

例5(2020Ⅱ卷第9题)我国新冠肺炎疫情进入常态化，各地有序推进复工复产，下面是某地连续11天复工复产指数折线图(图2)，下列说法正确的是( )．

图2

A．这11天复工指数和复产指数均逐日增加

B．这11天期间，复产指数增量大于复工指数的增量

C．第3天至第11天复工复产指数均超过80%

D．第9天至第11天复产指数增量大于复工指数的增量

例5是以2020年的后新冠肺炎疫情时期各地复产复工为背景，考查的是统计图的识别，借助统计图的分析来反映数据分析能力．随着日期推移，复产复工指数在波动上升，反映了我国疫情处理卓有成效，经济健康发展．

例6(2021Ⅰ卷第18题)某学校组织“一带一路”知识竞赛，有A, B两类问题．每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题冋答，若回答错误则该同学比赛结束；若回答正确则从另一类问题中再随机抽取一个问題回答，无论回答正确与否，该同学比赛结束． A类问题中的每个问题回答正确得20分，否则得0分；B类问题中的每个问题回答正确得80分，否则得0分．

己知小明能正确回答A类问题的概率为0.8，能正确回答B类问題的概率为0.6．且能正确回答问题的概率与回答次序无关．

(1)若小明先回答A类问题，记X为小明的累计得分，求X的分布列：

(2)为使累计得分的期望最大，小明应选择先回答哪类问题？并说明理由．

例6以当时国家推动发展的“一带一路”为背景，组织有关“一带一路”的知识竞赛．结合时政，使学生在解决问题的同时了解我国发展战略，促进共同发展，实现共同繁荣．

4.4 强调模型思想，凸显数学的应用价值

建模思想的形成是学生体会和理解数学与外部世界联系的基本途径[8]，并且模型的建立与知识在现实生活中的应用直接相关．新高考全国卷较关注数学模型，考查学生面对随机的数据选择合适的概率、统计模型来解决问题，体会概率与统计的模型思想，感受统计知识的应用价值．

例7(2020Ⅱ卷第19题)为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的PM2.5和SO2浓度(单位：μg/m3)，得下表：

PM2.5, SO2[0, 50](50, 150](150, 475][0, 35]32184(35, 75]6812(75, 115]3710

(1)估计事件“该市一天空气中PM2.5浓度不超过75，且SO2浓度不超过150”的概率；

(2)根据所给数据，完成下面的2 × 2列联表：

PM2.5, SO2[0, 150](150, 475][0, 75](75, 115]

(3) 根据(2)中的列联表，判断是否有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关？

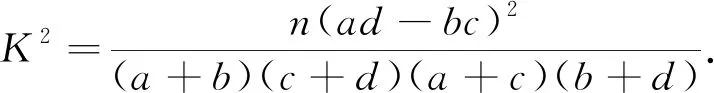
P(K2≥k)0.0500.0100.001k3.8416.63510.828

例7以空气质量检测为背景，展示不同PM2.5和SO2浓度的天数，体会数据的随机性．该题的设置考查学生利用相关概率与统计模型来分析随机现象，感受概率与统计模型在生活中的应用，提高学生的统计思维．

5 教学启示

5.1 注重情境创设，凸显学科育人目标

数学学科育人主要包括发展学生数学核心素养，增强学生发现和提出、分析和解决问题的能力．[9]学生获取数学核心素养与提高“四能”依赖于经验的积累，而经验均植根于情境之中，新高考概率与统计试题的呈现均配有相应的问题背景情境，引导学生利用概率与统计知识来进行问题的解决．教师在教学过程中，应特别注重情境对学生解决概率统计问题的影响，根据考查内容创设合适的问题情境，激发学生学习兴趣，落实数学学科育人目标．

5.2 注重模型思想，体会统计的应用价值

数学模型的建立是数学应用的重要途径，并且统计建模与数据分析的应用直接相关．新高考全国卷着重考查概率与统计的模型思想，要在题干中识别并利用相应的数学模型来解决问题．教师应注重概率与统计模型的教学，利用现实生活中跨学科的、未经处理的一手案例来促进学生对概率与统计知识的理解，培养学生的建模能力和对概念与模型的辨识能力，体会统计的应用价值．

5.3 注重数学实验教学，积累数学活动经验

数学实验利用学生的亲生经历，加强学生对随机思想、统计思想的认识．[10]新高考全国卷的简答题比较关注概率的随机思想，利用相关知识分析随机现象．教师要充分利用各种资源，增设数学实验，增加学生对随机现象的亲身体验，引导学生积极参与具体随机事件的产生和发展过程，在大量的重复试验中分析数据的规律，感知随机现象的不确定性，加深对概率和随机性的理解．对于随机现象的试验，教师可以尝试进行计算机随机模拟试验的教学，激发学生的学习兴趣，提高课堂教学效率．

5.4 开展项目式学习，培养数据分析观念

基于案例、问题的项目化学习有利于学生数据分析观念的发展．[11]同时，统计教学要求学生在教师的引导下经历完整的数据分析过程．新高考全国卷借助现实情境，考查学生的数据分析素养与知识的应用．教师应围绕数据分析过程这一主线，开展项目式学习，以课内课外相结合的方式，带领学生经历调查收集数据、整理分析数据、交流和解释数据、质疑和反思结论、形成数据分析活动报告的数据分析全过程，让学生在经历统计活动的过程中逐步培养数据分析观念．