同题异构课的案例对比分析
席建颖
摘要:同课异构是指同一个教学内容,不同教师运用不同的教学方法或同一教师运用不同的教学方法,根据现有的教学环境、自身的理解和学生的实际情况,实施不同的教学设计,达到同一个教学目标的教学活动。笔者于2020年12月1日至2020年12月13日期间对《5.6.1匀速圆周运动的数学模型》试教5次,并于2020年12月14日正式比赛,通过多次磨课上课,让我清楚地看到对同一教材内容的不同处理、不同的教学策略所产生的不同的教学效果,使我对如何落实新课标理念,发展学生数学核心素养有一个新的认识.以下是笔者对其中一次试教课(A课)和正式比赛课(B课)的授课情况的对比分析.
关键词:同课异构;数学建模;核心素养
一、两次课的教学过程简介
A课(试教课)的授课过程
(一)创设情境,提出问题
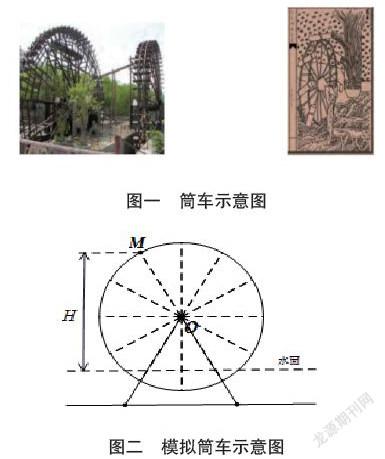
筒车筒车是一种用来浇灌农田的工具,它以水流为动力,非常环保,在当前的农业生产中还有非常广泛的应用(如图一)。
问题1:若是在水量一定的情况下,筒车在运动时的每个水桶可看作是匀速圆周运动。问:如何用函数模型来表示水面与盛水筒(视为质点)的距离及时间的关系?
(二)抽象问题,建立模型
问题2:筒车运动模型中,盛水桶的运动周而复始,具有周期性,因此可以考虑用三角函数模型来刻画它的运动规律,如果将筒车抽象成圆,盛水桶抽象为圆上的点(如图二),经过时间后盛水桶距离水面的高度(在水面下则为负)与哪些量有关?它们之间有怎样的关系呢?
学生需要先自行作图,而后结合信息思考,最后回答相应问题,以师生合作的形式展开学习。在他们思考时,教师要给予适当引导,帮助其分析题目中各个变量间的关系,比如转轴中心与水面的间距,筒车的半径,筒车转动的角速度,盛水桶的初始位置及其对应的初始角;再引导学生寻求变量与之间的等量关系:
(三)实际应用,加深理解
摩天轮问题
(视频1:摩天轮简介)
“东湖之眼”摩天轮总高度为55m,其直径约为50m,它的内部设有28个座舱。在摩天轮开启后,它会以逆时针方向匀速旋转,游客在座舱到距离地面最近的位置进舱,转一周大约需要15分钟。
(视频2:问题1)
1.游客上座舱5min后距离地面的高度是多少?
学生作图,思考,回答问题
(视频3:问题2)
2.再经过多少分钟,游客能达到上座舱6min时距离地面相同的高度?
学生作图,思考,回答问题
(视频4:问题3)
3.在摩天轮转动一周的过程中,相邻两个座舱A和B距离地面最大高度差是多少?
学生作图,思考,回答问题
4.课堂小结,布置作业
B课(正式课)的授课过程
1.创设情境,提出问题
播放“东湖之眼”摩天轮视频
同学们,你们曾将有过乘坐摩天轮的经历吗?接下来,你们想对摩天轮了解更多吗?在我们进一步的了解这个摩天轮之前,我们首先来研究下摩天轮的运动规律!
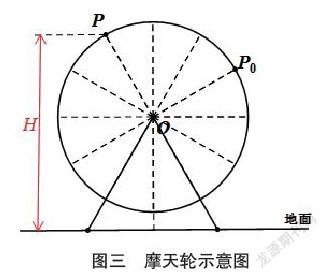
问题:摩天轮的每个座舱都作匀速圆周运动,用圆表示摩天轮,用点表示摩天轮的座舱,将摩天轮抽象为一个几何图形,如图三所示。假设摩天轮的某个座舱M经过时间t,从初始位置P0旋转到P,点P距离地面的高度H,思考以下问题:
(1)H与哪些量有关?(这些量请用字母表示)
(2)这些量之间有什么关系?请推导并用函数表达出来。
针对以上问题,小组合作交流,教师请部分小组代表分享研究结果,教师适当点评。
教师追问:(1)为什么会与摩天轮半径,中心到地面的距离,角速度以及初始角有关?请就其中一个实施解释。
(2)在求解的关系中我们利用了什么?
(3)以中心为原点建系相对于以地面为轴以过中心且与地面垂直的直线为轴建系有什么优势?为什么?
2.抽象问题,建立模型
同课A
3.应用模型,解决问题
问题设置同课A,不过课堂组织采用了小组合作交流,学生代表展示,教师点评的模式。
4.课堂小结,作业布置
二、两次课教学情况的对比分析
(一)教学设计的对比
两次授课流程大致一样,都包括:创设情境,引出问题;抽象问题,建立模型;应用模型,解决问题;课堂小结,作业布置四个部分,所选的问题也基本一样.这两次课主要的区别在于引出问题中创设的情景,A课选择的是中国古代水利灌溉工具“筒车”引出问题,这样做尊重教材,有利于中国古代农耕文化的传播,可是“筒车问题”远离学生生活,学生对其非常陌生,并不感兴趣,在探索“筒车问题”的过程中课堂气氛比较沉闷,而B课选择的是“摩天轮”引出问题,贴近学生生活,更易引起学生的学习主动性和好奇心,故而课堂气氛比较活跃。并且通过“摩天轮”引出问题也使得课堂首尾呼应,前后一致(最后是解决“摩天轮问题”)。
(二)授课目标达成的对比
授课目标是授课的方向,达成授课目标是授课的关键。
这两次课的授课目标均为:通过实际问题抽象出数学问题,针对数学问题建立函数模型,并能利用这一模型解决具有圆周运动特征的实际问题。两次课授课目标都实现了,但是目标实现的过程中两次课侧重点不同。A课側重于讲授,比如在学生并没有探索“盛水筒(视为质点)距离水面的相对高度与时间的关系”前,便告诉了学生“盛水筒运动具有周期性,可以应用三角函数模型来刻画”,在探索“经过时间后盛水桶距离水面的高度(在水面下则为负)与哪些量有关?”的过程中,给学生思考的时间比较少,基本上是直接告诉了学生“与有关系的量为”,而后不少学生轻松地写出了函数模型,这个过程看似很流畅,但学生建模思维难度低,缺少深层次的思维。而B课侧重于知识的形成,在未告知学生用哪种函数模型“刻画摩天轮座舱到地面的高度与时间的关系”情况下,给学生充足时间探究“H与哪些量有关?为什么有关?这些量之间有什么关系?在推导关系的过程中你利用到了什么知识?”这些问题,学生在深入思考这些问题的过程中逐步获得函数模型,函数模型是学生合作推理出来的,悟出来的。
(三)数学建模核心素养落实的对比
《2017版新课标》指出,数学建模素养是对现实问题实施抽象,用数学语言表达问题、用数学知识与方法构建模型解决问题的过程。主要表现在从数学的视角发现和提出问题,建立模型,求解模型,应用模型解决实际问题。就本课例而言,B课相对于A课对数学建模这一核心素养落实更加彻底。例如在应用模型解决实际“摩天轮问题2:再经过多少分钟,游客能达到上座舱6min时距离地面相同的高度?”中,A课中学生利用几何法即圆的对称性求出问题的结果后就进入了问题3的探究,这仅仅是为了“解题”而“解题”,对学生的数学建模素养发展无益。而B课中笔者并未避重就轻,引导学生应用所建立的三角函数模型去解决问题,强化了学生应用三角函数模型的意识,发展了学生的数学建模素养,给学生埋下了“应用数学知识解决一类问题”的种子。
(四)授课理念的对比
“学生的学习活动不应该仅限于接受、记忆、模仿和练习,高中数学课程还应倡导自主探索,合作交流和阅读自学等学习数学的方式”,这是新课标的重要理念。在这两节课上,学生都是课堂的主体,他们在课上进行了积极、独立、自主思考,并通过亲自动手的方式对所学知识进行了实践,最后将成果展示、交流。但是相对而言A课采用的更多是启发引导下的讲授法,学生比较拘束,对学生不放心。而B课授课中采用问题探究式授课模式,学生通过独立探究活动、小组讨论修正、全班展示交流,展示探究方法和思维活动;教师通过交流追问、课堂评价,达成问题的解决。例如在应用模型解决实际“3.在摩天轮转动一周的过程中,相邻两个座舱A和B距离地面最大高度差是多少?”的过程中,A课笔者因担心求解函数最值过程过于复杂,仅仅让学生把函数解析式写出来,便草草了之。B课笔者在学生写出函数之后,给出参考公式,再让学生探讨如何根据所给公式求解函数最值,结果不少学生通过三角恒等变换求出了最值,体验了成功的快乐。
三、结语
高中教师由于考绩的压力或者为了赶进度,平时教学中往往直奔主题,缺乏知识方法的形成过程,这样可能短时间能够提高学生的成绩,但是不利于学生学习兴趣和能力的培养以及核心素养的形成。数学核心素养的生成不可能一蹴而就,它是一个需要不断坚持的过程,没有任何捷径可以走,它需根植于我们的日常授课中。在发展学生的核心素养时,我们要善于从生活取材,坚持让学生以探究的形式获取知识,通过高效地师生互动、生生互动强化他们的知识应用、理解水平,在这个过程中,学生们可以领悟到数学思想和解决问题的方法,这对其数学核心素养发展意义重大。
参考文献:
[1]丁灵.新课程教學设计案例——《圆周运动的实例分析》[J].教育,2015(006):140.
[2]陈金华.融合两版本教材的案例分析——以《圆周运动》单元教学为例[J].中学物理教学参考,2013(7):13-16.
[3]韦建志.高中数学“同课异构”教研活动的相关理论与案例分析[D].华中师范大学,2018.

