以“圆周率”为径，探“数学家”之温

卞元佳

摘要：数学书上资料卡片的意义何在？在教学中，我们会发现教师对此教学的忽视或者一读而过的草草了事，课后又给学生留下了什么？本文基于此现象，结合圆周长后“你知道吗”反思探究教学，摸索改进课堂教学，从基于学习起点，激发学生学习兴趣等方面入手，让学生完整地经历释疑解惑，文化浸润下的数学学习过程。

关键词：圆周率;数学家;数学文化

中图分类号：A 文献标识码：A 文章编号：（2021）-42-469

一、问题发现——数学文化“冰冷无痕”

教学片段：

师：听说过祖冲之吗？我们一起了解他们的研究。（ppt出示资料卡片）你们有什么感受？

生1：我感觉祖冲之很伟大。生2：我觉得，我们古人很厉害！

师：好，课上到这里，今天我们学会了圆的周长，你们还有什么疑问吗？

生3：我们能说圆的周长是直径的3.14倍吗？生4：（抢着说）不能，3.14是个近似数，老师刚才都已经说过了——近似数。

师：对呀，圆的周长应该是直径的π倍，计算时选用3.14。

思考：提到祖沖之，会想起圆周率，仅此而已吗？ 我们大多数教师教学习惯依附于教材，讲透、讲深，而后进行大量的习题演练，学生习惯于被动地接受，被动地回答教师的提问，认为只要掌握了知识点，会解题，就没有必要渗透数学文化。教师只看到了数学的“知识价值”，忽略了数学的“人文价值”，对数学所特有的文化教育价值的理解和把握不够适当。数学文化在《课程标准》中已被作为单独板块列出，也体现了他的特殊地位。所以我们教师要在教学中渗透数学文化。

二、价值细审—— “π”的育人价值

圆的周长的数学文化价值究竟在哪儿？答案源于“π”的研究。

（一）数学家的精神

有一种精神叫做“数学家的精神”，它是严谨、不断追求、执着探索……代名词。我们知道，为求π的值，人类走过了漫长而曲折的道路，它的历史是饶有趣味的。π的研究从实验测量法、割圆术、高等数学分析、计算机运用等，这些研究方法带有有明显的历史阶段性，这与数学发展水平密不可分。而每种方法的诞生定是在前人研究之上，为追求精密程度而另辟蹊径，创新思考，进而发现“新大陆”，成就数学的伟大。在历史的长河里，从阿基米德、刘徽、祖冲之、鲁道夫、欧拉等不同时期数学家们的研究故事里，我们是能够感受到他们执着的探索过程，科学的严谨态度，这正好完美诠释牛顿所说的“站在巨人的肩膀上”。今天我们所讲的圆周长计算公式“C=πd”是凝聚众人的智慧，来之不易的，而且“π”的研究至今仍未停歇，令我们为之震撼。上述中，无论从探究方法、探究精神还是探究成果都是可以给人以“温度”。数学文化彰显的是一部励志史、教育史和发展史，它使“冰冷”的数学有了“温度”感，充满了人文情怀。

（二）历史前进的车轮

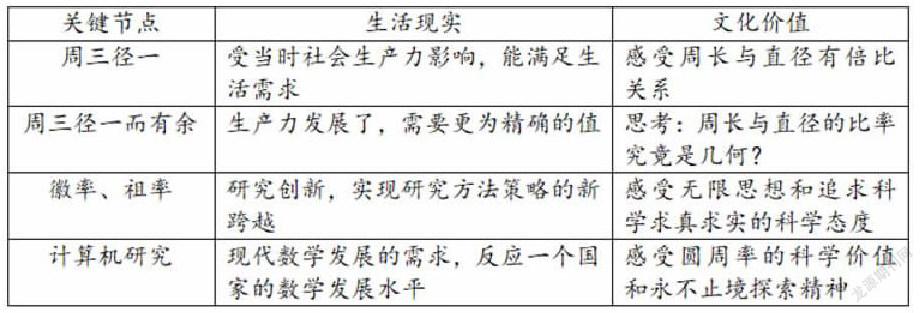
π的发展经历下表的历程。

从“周三径一”到“周三径一而有余”的矛盾，再到通过“割圆术”得到的“徽率”和“祖率“，乃至通过计算机在计算圆周率，这是历史发展的节点，也是历史前进的动力。波利亚在《数学的发现》一书中也强调：人类的后代学习数学应重走人类认识数学的重大几步。因此，笔者认为，将课堂教学展开的主线与圆周率产生发展的历史线索结合起来，让学生重走他们能走的、人类研究圆周率的关键几步。把这“关键几步”是需要像当作主菜一样精心“烹饪”，才显“丰盛”。

三、实践之感——走进历史，感受温度

数学是一种“文化”，它不仅具有传承知识的功能，还具有独特的育人功能。当数学文化浸润数学知识，进入课堂，融入教学时，我们的数学课堂就充满了生机与活力，就会通过文化层面让学生理解数学，爱上数学。因此在教材中捕捉到有价值的数学文化，服务于教学，服务于学生，让每个孩子提升数学素养，是我们当下教师的文化使命。圆周率的探索有着曲折而漫长的过程，它是人类共有的精神财富，结合数学史，能够让学生对圆周率的认识更加全面。故此，笔者设计了如下教学环节：

（一）周三径一有余

师：刚才提到的“周三径一”，魏晋时期的刘徽在公元263年给《九章算术》作注解时发现“周三径一”只是圆内接正六边形的周长和该圆的直径的倍数关系。我们一起来看。 PPT，后附图2（画外音）介绍，所以，周三径一有余！

（二）介绍割圆术

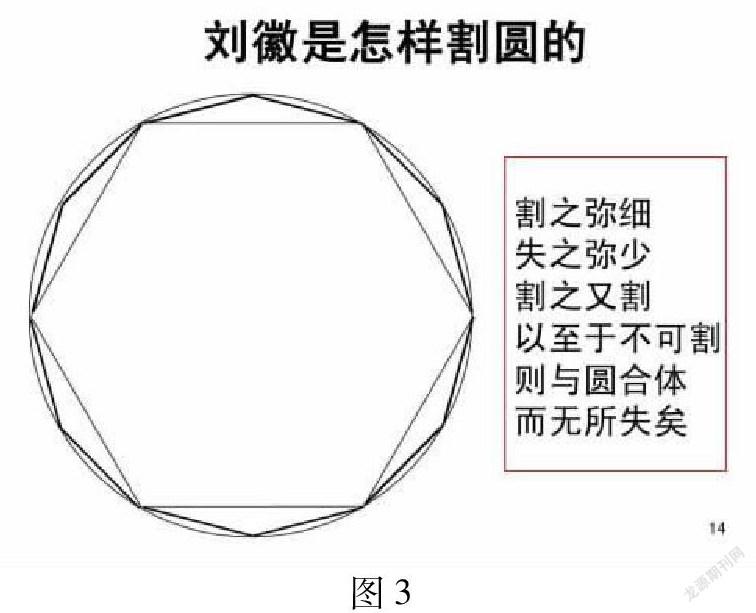
师：于是刘徽采用割圆术，将圆周长与直径的关系改进成了3.14倍，又称徽率。我们一起来看。比较（PPT动态展示，后附图3）：正12边形比正六边形周长相比，谁更接近圆的周长？

思考：如果继续分下去，想一想，如果我们这样一直分下去，会有什么发现呢？

解释：请一位同学读一读刘徽关于“割圆术的这段话。 “割之弥细，所失弥少，割之又割，以至不可割，则与圆周合体而无所失也。” 谁能懂一下这段话。

总结：通过这段话，我们可以理解“正多边形的边数达到无穷多时，正多边形的周长就是圆的周长。” 刘徽首创“割圆术”是中国古代极限观念的体现，他一生都为数学刻苦探索，学而不厌，给我们中华民族留下了宝贵的财富。

（三）介绍祖率

师：人类的对圆周长与直径的倍数关系研究并没有停止，请看，同学们都很熟悉——祖冲之。（直径3.33米的圆上分，在刘徽基础上继续分割正2 4576多边形，每条边仅有0.4毫米，而且你要知道当时就算工具的简陋无法想象，一旦出错就要重来）你是否有感想要说了？（他的探究精神值得我们学习）我们继续看人类的对圆周长与直径的倍数研究（PPT展示，后附图4）。

（四）介紹圆周率

师：至今，数学家们无论研究多少位小数，圆周长与直径的倍数总是这样的——（PPT动态依次呈现前一百位小数）。

观察：前一百位，你有什么发现？

生;无限不循环小数。

生：跟刘徽、祖冲之研究出来的前几位都是一模一样的，数字是固定的。

介绍：师：看来，圆的周长与直径的倍数关系可以写成——（板书：C÷d=3.1415926…），数学上，我们把这个倍数叫做圆周率，由于它既不循环又写不完，怎么办呢？所以数学上就用π这个符号表示。

上述各个教学环节通过倾听、阅读、理解、思考、交流有关历史资料，让学生在体会探索圆周率的过程中，自然而然萌生一种民族自豪感，体会到人类对真理的追求永无止境。在介绍周三径一有余环节，学生通过观察，结合画外音的介绍，通过演绎推理形式锁定圆周长的范围，为之前的实验测量的结果是否合理提供了无可置疑的科学依据。介绍祖率时，穿插了祖冲之年代计算工具简陋、计算量繁杂、操作不易等困难，对学生的触动是震撼的，他伟大无需更多言语，相信学生能够真切体会到。同时，割圆术的介绍提升了学生的认知，亲身经历正多边形逼近圆的过程，在感受研究曲线的新方法的同时，从心灵深处收到触动，强烈感受到数学的文化魅力与价值。还有，圆周率前100位数字的一次动态出现，让学生观察发现其是一个固定的值，完成有意义的建构学习。在讲历史、学历史的过程中，学习人类解决问题的智慧，为学生站在巨人的肩膀上形成自己的数学活动经验和解决问题的智慧埋下创新的种子。至此，找到了数学文化“教书又育人”的均衡效果，有效落实学生的核心素养。

四、结束语

数学家精神蕴含着数学文化之魂，数学文化的内涵不仅表现在知识本身，还寓于它的历史中，数学是一种历史存在。在教学中通过对数学文化内涵的学习，数学文化的存在价值及数学文化的民族性和世界性的认识，让学生全面感知数学既是一门知识、语言、自然与社会联系的工具，又是思想方法和具有审美特征的艺术的集合体。我们要在数学教学中渗透数学文化，精心创设教学情境，为学生学习做好充分的课堂准备，才能将数学文化的魅力真正融入到课堂、融入到教学，才能让学生进一步喜欢数学、热爱数学，从而主动探索获取知识。

参考文献

1.吴文俊主编.中国数学史大系.北京：北京师范大学出版社，1998

2.钱宝琮校点.算经十书.北京：中华书局，1963

3.李文林主编.数学史概论.北京：高等教育出版社，2000

4.李文林主编.数学珍宝——历史文献精选.北京：科学出版社，1998