基于经典和Riesz导数的分数阶广义Birkhoff系统的Noether定理

周 颖,张 毅

(1.苏州科技大学 数学科学学院,江苏 苏州 215009;2.苏州科技大学 土木工程学院,江苏 苏州 215011)

Birkhoff力学,作为Hamilton力学的自然推广,是迄今最一般可能的一个力学[1,2]。完整力学和非完整力学均可纳入Birkhoff力学[2]。广义Birkhoff力学[3]是由梅凤翔在Birkhoff系统动力学的研究基础上提出并创建而成,其基础是广义Pfaff-Birkhoff原理和广义Birkhoff方程。微分方程的Birkhoff化有时很难实现,广义Birkhoff方程由于增加了一个可调节的附加项,使微分方程很容易化为广义Birkhoff方程。Birkhoff和广义Birkhoff系统动力学及其对称性研究近十年来有了一些新的进展[4-12]。

分数阶微积分,作为一个有效的数学工具,为描述具有摩擦或其他耗散过程的非保守系统提供了一个新的方向[13-15]。Frederico和Torres[16,17]最早将经典Noether定理及其证明的时间重新参数化方法推广到分数阶Lagrange系统,通过定义分数阶守恒量建立了分数阶Noether定理。Bourdin等[18]给出了分数阶Lagrange系统的离散分数阶Noether定理,通过其提出的“传递公式”将分数阶守恒量表达成显形式。2016年,Frederico等[19]研究并给出Lagrange函数依赖于经典和Caputo导数的非保守系统的Noether定理。但是这些研究都限于分数阶Lagrange系统或分数阶Hamilton系统。分数阶Birkhoff系统是一类更广泛的系统,包含了分数阶Lagrange系统、分数阶Hamilton系统等[20,21]。近年来,分数阶Birkhoff系统的Noether对称性与守恒量的研究成为一个热点并取得重要进展[22,31]。但是,迄今研究尚未涉及经典和分数阶导数联合的分数阶Birkhoff系统。本文将提出并证明基于经典和Riesz导数的分数阶广义Birkhoff系统的Noether定理,利用“传递公式”给出守恒量的显形式。

1 经典和Riesz-Riemann-Liouville导数下分数阶广义Birkhoff系统的Noether定理

关于分数阶微积分的定义及基本性质,参见文献[13,22]。

1.1 分数阶广义Birkhoff方程

经典和Riesz-Riemann-Liouville导数下的Pfaff作用量为

(1)

于是,分数阶广义Pfaff-Birkhoff原理可表示为

B(t,aν))+δ′W]dt=0

(2)

且满足交换关系

(3)

和边界条件

δaμ|t=t1=δaμ|t=t2=0

(4)

由式(2)和式(3),容易导出

μ=1,2,…,2n

(5)

以及相应的横截性条件

(6)

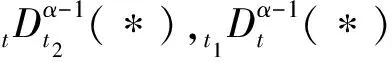
1.2 分数阶Noether定理

根据时间重新参数化方法[16],定理及其证明可分两步。

(1)第一步,在时间不变的特殊无限小变换下,建立并证明Noether定理。

假设在特殊无限小变换[16]

(7)

的作用下,对任意积分区间[T1,T2]⊆[t1,t2],始终成立

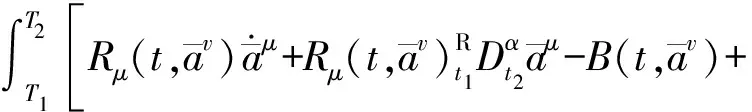
(8)

式中:ΔG=εG,G(t,av)是规范函数,则此不变性可称为式(5)分数阶广义Birkhoff系统的Noether对称性。

若生成元ξμ满足如下分数阶Noether等式

(9)

则式(7)对应于式(8)意义下的Noether对称性。

实际上,由式(8)并考虑到积分区间[T1,T2]的任意性,可得

(10)

将式(10)等号两边对ε求导,并令ε=0,有

这就是式(9)的Noether等式。

利用式(5),式(9)也可表示为

(11)

式(11)可写成

(12)

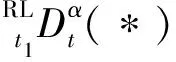
下面,引入分数阶传递公式。文献[18,19]中证明了如下结果:

(13)

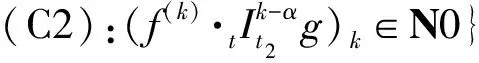
(14)

利用传递式(13),令g=Rμ,f=ξμ,得到

(15)

同样地,若令g=ξμ,f=Rμ,则有

(16)

于是有

定理1如果式(7)对应于式(8)意义下的Noether对称性,且函数Rμ和ξμ满足传递公式的条件(C1),则表达式

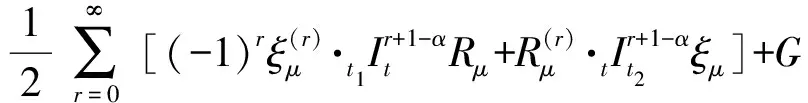
(17)

是式(5)分数阶广义Birhoff系统的Noether守恒量。

(2)第二步,在时间变更的一般无限小变换下,建立并证明Noether定理。

假设在一般无限小变换[16]

εξμ(t,av)+o(ε)

(18)

的作用下,对任意积分区间[T1,T2]⊆[t1,t2],始终成立

(19)

则此不变性可称为式(5)分数阶广义Birkhoff系统的Noether对称性。

若生成元ξ0和ξμ满足如下分数阶Noether等式

(20)

则式(18)对应于式(19)意义下的Noether对称性。

实际上,由式(19)可得

(21)

由积分区间[T1,T2]的任意性,可得

(22)

类似于文献[21]的推导,有

(23)

将式(23)代入式(22),并将式(22)等号两边对ε求导,并令ε=0,易得式(20)。

定理2如果式(18)对应于式(19)意义下的Noether对称性,且函数Rμ以及生成元ξ0和ξμ满足传递公式的条件(C1),则表达式

(24)

是式(5)分数阶广义Birkhoff系统的Noether守恒量。

证明取关于时间t的李普希茨变换 [t1,t2]t|→σf(λ)∈[σ1,σ2],当λ=0时,满足分数阶Pfaff作用量在上述变换作用下成为

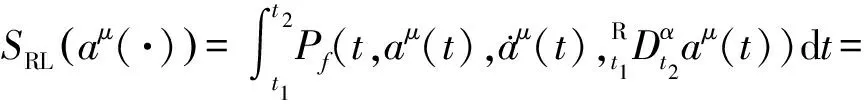
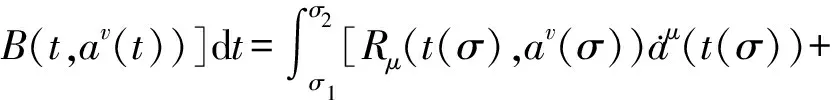
B(t(σ),av(t(σ))]t′σdσ

(25)

类似于文献[29]可得

(26)

将式(26)代入式(25)可得

(27)

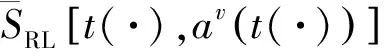
(28)

当λ=0时,有

(29)

因此,可得到

(30)

以及

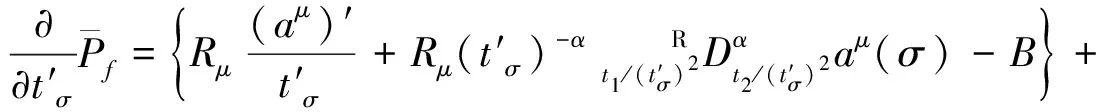
(31)

将式(31)和(30)代入式(28)即得式(24)。证毕。

定理1和定理2称为经典和Riesz-Riemann-Liouville导数下分数阶广义Birkhoff系统的Noether定理,其证明采用了时间重参数化方法。当ξ0=0时,定理2退化为定理1;如果分数阶项不存在,则定理1和定理2给出经典广义Birkhoff系统的Noether定理[3]。

2 经典和Riesz-Caputo导数下分数阶广义Birkhoff系统的Noether定理

2.1 分数阶广义Birkhoff方程

经典和Riesz-Caputo导数下的Pfaff作用量为

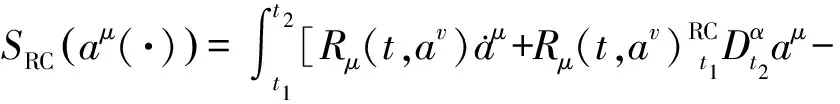
B(t,av)]dt

(32)

于是,分数阶广义Pfaff-Birkhoff原理可表示为

B(t,aν))+δ′W]dt=0

(33)

且满足交换关系

(34)

和边界条件

δaμ|t=t1=δaμ|t=t2=0

(35)

由式(33)和式(34),容易导出

μ=1,2,…,2n

(36)

以及相应的横截性条件

(37)

由式(35)可知式(37)恒成立。式(36)称为经典和Riesz-Caputo导数下的分数阶广义Birkhoff方程。

2.2 分数阶Noether定理

(1)第一步,在时间不变的特殊无限小变换下,建立并证明该系统的Noether定理。

假设在特殊无限小变换[16]

(38)

的作用下,对任意积分区间[T1,T2]⊆[t1,t2],始终成立

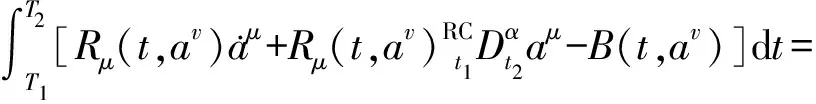
(39)

则此不变性可称为式(36)分数阶广义Birkhoff系统的Noether对称性。

若生成元ξμ满足如下分数阶Noether等式

(40)

则式(38)对应于式(39)意义下的Noether对称性。

类似于定理1,容易得到如下定理。

定理3如果式(38)对应于式(39)意义下的Noether对称性,且函数Rμ和ξμ满足传递公式的条件(C2),则表达式

(41)

是式(36)分数阶广义Birhoff系统的Noether守恒量。

(2)第二步,在时间变更的一般无限小变换下,建立并证明Noether定理。

假设在一般无限小变换[16]

(42)

的作用下,对任意积分区间[T1,T2]⊆[t1,t2],始终成立

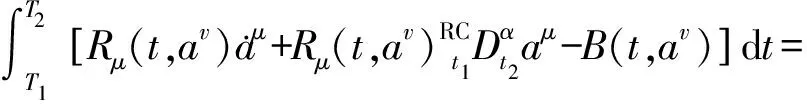
(43)

则此不变性可称为式(36)分数阶广义Birkhoff系统的Noether对称性。

若生成元ξ0和ξμ满足如下分数阶Noether等式

(44)

则式(42)对应于式(43)意义下的Noether对称性。

类似于定理2,我们有如下定理。

定理4如果式(42)对应于式(43)意义下的Noether对称性,且函数Rμ以及生成元ξ0和ξμ满足传递公式的条件(C2),则表达式

(45)

是式(36)分数阶广义Birkhoff系统的Noether守恒量。

定理3和定理4称为经典和Riesz-Caputo导数下分数阶广义Birkhoff系统的Noether定理,其证明采用了时间重参数化方法。当ξ0=0时,定理4退化为定理3;若分数阶项不存在,则定理3和定理4给出经典广义Birkhoff系统的Noether定理[3]。

3 算例

研究Hojman-Urrutia例[32]。根据Santilli的研究[1],Hojman-Urrutia例具有Birkhoff表示,但是不具有Lagrange结构,原因在于其本质上是非自伴随的。Hojman-Urrutia问题也可表示为广义Birkhoff系统,即有

(46)

根据式(5),在经典和Riesz-Riemann-Liouville导数下系统的运动微分方程为

(47)

式(20)Noether等式给出

(48)

式(48)有解

(49)

式(49)对应系统的广义准对称变换。由定理2可得

(50)

式(50)是由Noether对称性式(49)导致的守恒量。当α→1时,式(50)成为

IN=2(a2+a3)

(51)

式(51)是经典广义Birkhoff系统的守恒量。

4 结束语

分数阶Birkhoff系统动力学研究是近年来分析力学研究的一个新方向。由于Birkhoff力学的普遍性,分数阶动力学模型的记忆性和非局域性,非保守和非完整系统的分数阶Birkhoff动力学研究具有重要意义。

本文主要工作如下:(1)提出并研究经典和Riesz导数下分数阶广义Birkhoff系统动力学,建立了此情形下的变分原理和动力学方程;(2)研究了经典和Riesz导数下分数阶广义Birkhoff系统的Noether对称性与守恒量,用时间重新参数化方法证明了Noether定理;(3)利用传递公式给出了分数阶Noether守恒量的显形式。

本文的主要结果是给出的4个定理,以及式(2)和(33)的原理、式(5)和(36)的方程、式(24)和(45)的守恒量。当分数阶导数项不存在时,定理退化为经典广义Birkhoff系统的Noether定理。