一种基于起伏地形与辐射电场分布相似性的指纹辅助定位方法仿真研究

魏正桓 唐万春 李保珠 孙芮

（1.南京师范大学物理科学与技术学院，南京 210023；2.南京师范大学电气与自动化工程学院，南京 210023；3.江苏省地理信息资源开发与利用协同创新中心，南京 210023）

引 言

随着现代信息通讯的蓬勃发展，涌现出了各式各样的定位技术.其中，基于接收信号强度指示器(received signal strength indication, RSSI)的指纹定位技术因其具有不需要参考测量点、定位精度相对较高等优势而得到了广泛的应用[1-3].其工作过程主要分为两个阶段：离线采集阶段和定位阶段.离线阶段，通过现场调查采集测试区域的RSSI建立指纹图谱[4]，即建立场强地图[5-6]；定位阶段的主要工作是将移动端在待测点采集到的定位信号特征与RSSI指纹库中的数据进行匹配，得出待测点所在的位置信息.

但是，文献[7]指出，指纹定位技术的缺点在于前期离线建立指纹库阶段时调查困难，很难自适应于环境变化较大的场景.在离线阶段需要建立场强地图，如果难以确定场强测量区域的位置则无法进行后续的定位工作.对于小范围场强地图的构建，有学者提出了采用反演模式的电波传播模型来构造用于定位的场强地图[8-10].这种方法虽然在室内定位取得了不错的效果，但难以适用于大尺度的山区复杂地形，山区地形的起伏程度对于电波传播的影响在模型中往往被忽略.

由于山地地区的地理环境复杂，实地测量时容易出现难以确定场强测量区域位置信息的问题.此时，电波在传播过程中会受到距离传播损耗、地形阴影慢衰落噪声和多径效应快衰落噪声的影响[11].对于同一媒介的地理环境，地形起伏对电场场值分布的影响主要体现在两个方面：一方面，电波传播过程中在近地面区域上形成了不规则的干涉条纹，而且电波经过空间叠加后增强的区域位置也不相同，且变化趋势与地形的变化趋势比较相近[12]；另一方面，凸出的地表会造成遮挡，电场场值与自由空间只因距离造成传播损耗的电场场值有较大不同.因此，在只获得了地理环境中某一测量区域的电场场值分布的情况下，如何定位这些缺少位置信息的场强测量区域是一个亟待解决的问题.

本文提出了一种基于起伏地形下辐射电场分布特性的定位方法，为在山地地区构建场强地图时遇到的困难提供了一种新的解决方案.该方法利用电场场值在发射源附近快速衰减的特性，结合起伏地形的高度变化情况，通过匹配算法对位置信息未知的场强测量区域进行定位.这种方法简单方便，不但适用于没有测向设备的地区，也可以作为有测向设备的地区进行定位时的一种辅助手段.

1 天线模型与地理建模

为充分认识地理环境中电磁场分布与地形地貌的关系，本文以应用最广泛的一类天线——半波偶极子天线(l=λ/2，l为天线总长度，λ为工作波长)为例构建物理模型，分析其在大尺度地理空间中的电场分布特点.

另外，二维随机粗糙面是对真实、复杂地理环境的一种模拟方式，其电磁散射特性在海洋、陆地遥感和军事领域的背景杂波分析中具有广泛的应用.本文使用蒙特卡洛方法生成二维随机粗糙面来模拟复杂、起伏的地形[13-14].地形均方根高度δ、相关长度l是常用的描述粗糙地的统计参量，这些参量以波长λ为度量单位.

粗糙面任一点高度为f(x,y)，将其用离散傅里叶变换表示为

同时，为了保证地形高度为实数，F(m,n)必须满足关于原点共轭对称：

这里选择生成二维高斯粗糙面，其功率谱函数为

式中：δ为地形的均方根高度；lx,ly分别为x,y方向的相关长度；N(0,1)表示满足均值为0，方差为1的高斯分布序列中的一个随机数；Km,Kn分别为粗糙面x,y方向上的空间频率离散点；Lx,Ly分别为二维随机粗糙面在x,y方向的总长度，满足

相关长度l用来判断粗糙面上两点间是否相互独立，当两点间的水平距离足够大时，它们之间互不影响.均方根高度δ和相关长度l的变化，决定了粗糙面的粗糙度，从而改变地形的起伏程度.

2 起伏地表与辐射电场分布的相似性研究

地面为平坦地面时不论何种天线位置都无法找到比别的位置更高的地方，而地形起伏度越大越有可能找到高地，所以随着地面起伏度的增加位置标准的作用越明显[15].因此，本文选择将发射天线置于高地，以便研究起伏地形和辐射电场分布的相似性，如图1所示.图1(a)为在均方根高度 δ =20λ、相关长度lx=ly=15λ地形的高地放置一个半波偶极子天线作为发射天线，并以天线位置为原点建立三维坐标系x′y′z′.图1(b)为在该地形下的辐射电场场值分布情况.

图1 地形高程图及其电场场值分布情况Fig.1 Topographic elevation map and its electric field distribution

在实际应用中，发射天线一般会选择放置在高地，以保证能有较好的接收信号.随着地形起伏度的增加，发射天线的位置对传输损耗的影响增加，因为

在起伏地表下，空间中辐射电场的变化趋势与地形起伏有相似性，这种相似性体现在以发射源为中心的纵向剖面(以x′o′z′平面、y′o′z′平面为例)和横向水平面(x′o′y′平面).图1(c)为图1(a)中红框区域内的地形变化和电场场值变化的比较图，上层为地形高度分布，下层为电场场值分布，图1(d)为电场分布的放大图像.为便于观察，数据进行了归一化处理.

在纵向剖面(以x′o′z′平面、y′o′z′平面为例)具体表现为：电场场值在发射天线附近产生较大的衰减；由高到低的地势也可看作是地形高度的衰减.这两种衰减都反映了剖面处数值变化的斜率，即三维空间中沿此方向的梯度.如图2所示为不同高度天线下的电场场值分布纵向剖面图，反映了天线高度发生变化时，某一发射天线所在x' 方向、y' 方向的电场场值分布的变化.

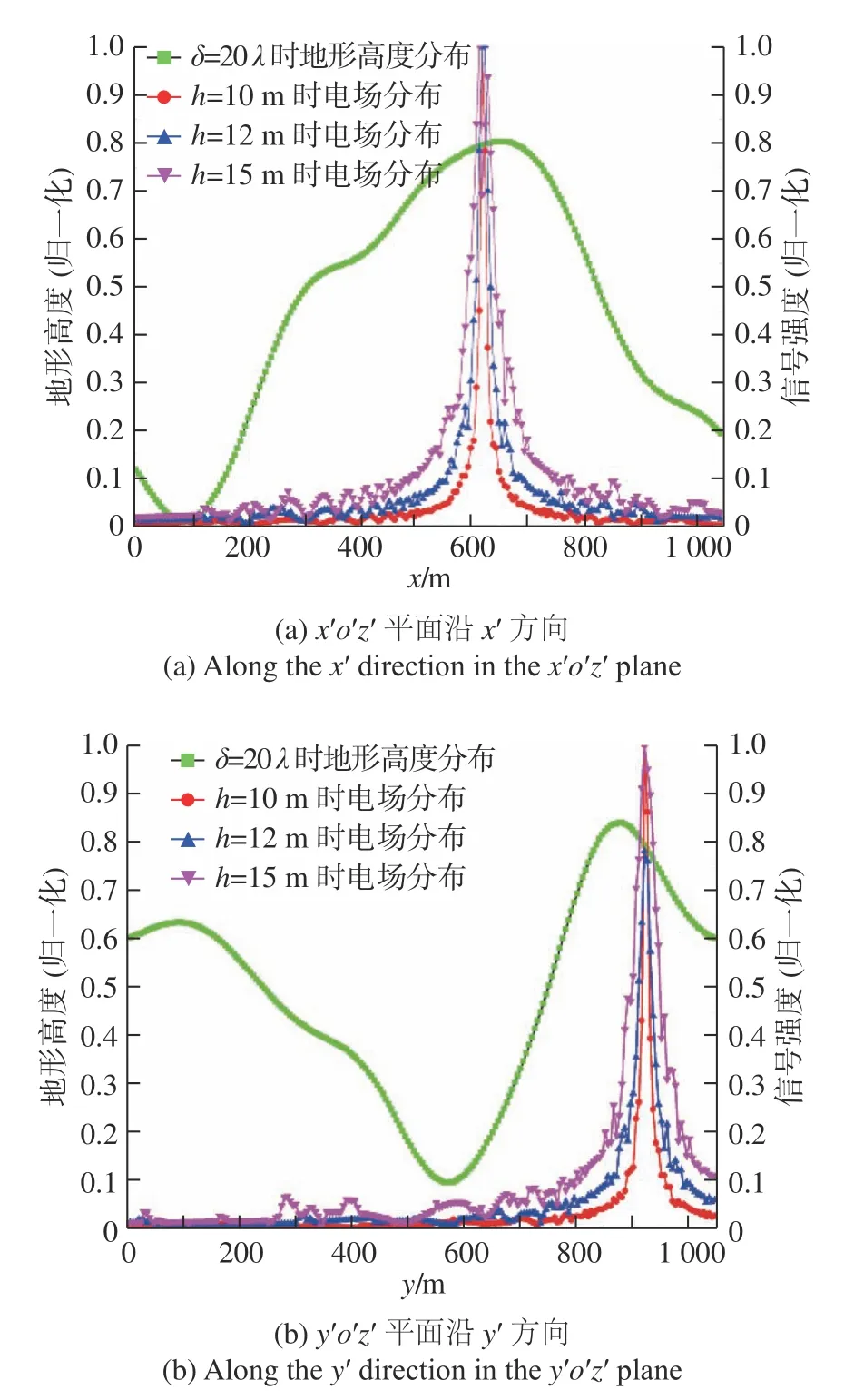
图2 不同高度天线下的电场场值分布纵向剖面图Fig.2 Longitudinal profile of electric field distribution under antennas with different heights

在横向的水平面上( x′o′y′平面)地形的影响体现为对电波传播的阻挡作用.图3为在同一地形轮廓下辐射电场在不同均方根高度下的分布情况.对照图1中的地形，可以发现由于地形的阻挡，此时的电场分布与自由空间中电场分布有明显差异：随着地形均方根高度 δ的增加，干涉条纹的形状由自由空间中“规整的圆形”变得越来越扭曲，这是受到了邻近山峰阻挡的影响.

图3 不同均方根高度下辐射电场的分布Fig.3 Distribution of radiation electric field under different root mean square heights

经过大量仿真实验发现这种阻挡影响是广泛存在的.对于不同的地形地貌，干涉条纹形状均受到邻近山峰或山谷的显著影响，而在未受阻挡的区域，干涉条纹的形状与地形等高线的形状存在相似性.如图4所示为辐射电场在不同地形环境下的分布情况，标注红框的部分可以直观地看到干涉条纹形状和地形等高线的相似情况.对于图4(a)、(b)红框中部向下凸出的条纹呈现相似的情况，这是由于发射天线下侧为低地，电波传播不会受到山峰的阻挡；而对比图4(c)、(d)可以发现，红框左下角的电场分布受到右上角的高地的阻挡，其干涉条纹与右上角高地的等高线分布相似.

图4 不同地形环境下辐射电场的分布Fig.4 Distribution of radiation electric field in different terrain environments

综上，在相关长度较大的地形上，辐射电场的电场场值在发射源附近快速衰减的变化趋势与地形起伏的高度降落的变化趋势相近.同时，在水平面上观察到的干涉条纹形状与地形轮廓(即等高线)的形状相似.因此，在仅有地形高程数据的情况下，可以通过这两种规律，定位那些缺失位置信息的场值测量区域.

3 定位算法

实现在地理环境中查找到场强测量区域的位置，须采用匹配算法.根据上文中总结的辐射电场场值在纵向剖面和横向水平面上与地形起伏变化的相似性，本文设计了一种以二维相关系数来衡量相似度的匹配算法.

在取得地形高程值矩阵和测量区域电场场值矩阵后，将电场场值E0(m,n)、 地形高度H0(M,N)通过以下归一化处理：

式中：m,n表示电场场值矩阵的行列数；M,N表示地形高度矩阵的行列数.取值区间为[0,1]，无量纲，进而消除了数据单位对相似性计算的影响.

电场场值相邻数据点之间的间隔大小对应实际地形中采样点间的距离，应尽量保证这个距离等于地形高程值采样点间的距离.因此，对电场场值的数据进行采样处理，使两个矩阵采样后相邻数据点间的间隔所反映的实际地形中采样点间的距离相等.采样后电场场值的矩阵记为模板矩阵E，整个地形的高程值矩阵记为被搜索矩阵G，图5为定位算法数据处理时的示意图.

图5 定位算法示意图Fig.5 Schematic diagram of positioning algorithm

模板矩阵E叠放在搜索矩阵G上平移，模板覆盖被搜索矩阵的区域称为子矩阵H，i，j为子矩阵H左上角在搜索矩阵G上的坐标，搜索范围为：1≤i≤M−m，1≤j≤N−n.本文选择二维相关系数来衡量模板矩阵E与子矩阵G间的相似度，模板匹配的二维相关系数的计算公式为

E与H的相似程度越高，二维相关系数R(i，j)越接近于1，在被搜索矩阵G中完成全部搜索后，找出R的最大值，其对应的子矩阵即为匹配目标.

综上所述，对于起伏地形下辐射电场的模板匹配定位算法流程如图6所示.

图6 基于模板匹配的定位流程Fig.6 Positioning process based on template matching

4 性能评价

本文用重叠率这种指标对定位结果进行评价.

考虑到随机粗糙面的地势起伏具有随机性，会造成在某些离实际位置较远的区域出现相似度的极值问题，因此有必要通过重叠率来描述匹配区域与实际截取区域的远近.重叠率反映模板区域和实际测试区域的重叠面积的大小，如图7所示.重叠率具体定义为重叠区域面积与两个区域总面积的比值，用Q表示，无量纲，表达式为

图7 重叠率示意图Fig.7 Schematic diagram of overlap ratio

5 仿真结果

设置均方根高度 δ=20λ ，相关长度lx=ly=15λ，通过蒙特卡洛方法模拟产生二维随机粗糙面，采样间隔1 m，以GeoTiff的数据格式保存，空间坐标(110.563 906 25°E，35.755 078 125°N)，生成数字高程图.

利用商用软件Wireless Insite进行仿真结果比较，选取观察面上的两个接收机，达到该点的传播路径分别为4条和3条.电波传播路径如图8所示，充分考虑了多径传播对本文中模型的影响.

图8 Wireless Insite电磁仿真软件中的电波传播路径Fig.8 Radio wave propagation path in Wireless Insite software

首先，将蒙特卡洛法生成的二维随机粗糙面(地形尺寸为1 050 m×1 050 m)导入到Wireless Insite中，然后在软件中设置地形材料为湿土地(εr=25,σ=2×10−2S/m)，发射天线高度为海拔+10 m，相应地设置发射天线的输入功率为47 dBm，接收天线采用垂直极化的全向天线，高度为海拔+9 m，测量点间距为5 m.由于地形模型的尺寸以电长度 λ为单位，因此天线工作频率的改变与地形参数的改变是相对的，改变天线频率即可认为地形参数也同时改变，这里选择偶极子天线工作频率为3 GHz，电长度λ 为1 m.

图9为地形上的匹配结果，发射天线空间坐标为(110.564 927 713 7°E, 35.751 315 155 7°N)，发射天线在研究区域中的坐标为(620, 920)，模板(电场测量区域)尺寸为300 m×300 m，模板中心坐标为(800,820)，如图10(a)所示.最终定位到的位置在地形图中用黑框区域表示(图10(b))，实际位置用红框区域表示(图10(c)).

图9 δ =20λ,lx=ly=15λ 地形的高程图Fig.9 Topographic elevation map ofδ=20λ,lx=ly=15λ

图10 算法测试Fig.10 Algorithm test

5.1 不同位置测量区域的仿真结果

根据模板位置、天线高度的不同组合进行多次仿真实验，用重叠率反映定位结果，统计其成功概率.设一次实验中成功定位的S1与S2间的重叠率不小于设置阈值时即为本次实验成功.定位成功率[16]为实验成功次数占总实验次数的比例，即

式中：Si为 在某一情况是否能成功定位；T为总的实验次数，设置为每组40次；Qthreshold为设置的重叠率阈值，设置为0.3.

图11为不同位置下的定位成功率.可以看出：对于不同起伏程度(不同地形均方根高度δ)的地形和不同海拔高度的发射天线的组合，随着地形起伏程度的增加，电场分布与地形分布的相似性增加，使得定位算法匹配的成功率提升；然而，当天线高度增加到一定程度时，接收机获得的信号强度也随之减小，导致电场分布与地形的相似性减小.

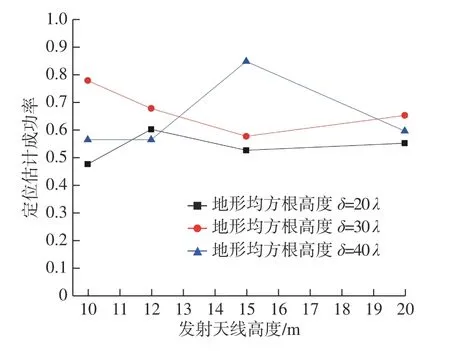
图11 不同位置下的定位成功率Fig.11 Location success rate at different positions

综上可见，本文方法的匹配定位成功率较高，可以很好地完成对缺失位置信息场值测量区域的定位，说明本文方法符合理论推导，具有可行性.

5.2 不同大小测量区域的仿真结果

为了比较模板大小对此定位算法的影响，保持截取的模板(电场测量区域)中心坐标为(800，820)，边长为100～400 m，同时改变发射天线的高度，进行仿真实验.图12所示为在发射天线高度为10 m、15 m和20 m的情况下，重叠率随模板边长变化的实验结果.可以得出：随着模板边长的增加，重叠率逐渐增加并维持在较高水平；发射天线的高度对这种定位算法也有重要的影响，随着发射天线高度的增加，模板边长在150～200 m时即可达到较高的重叠率，实现有效的识别.

图12 不同发射天线高度重叠率随模板边长的变化Fig.12 Overlapping rate under different conditions

5.3 其他地形下的仿真结果

得到较好的接收信号.仿真结果如图13所示，图(a)、(b)是在不同地貌的地形上进行随机取样的定位，重叠率为0.460；图(c)、(d)则是在起伏大一些的地形( δ=40λ)上进行的，此时重叠率为0.515.可以发现，在不同地形下都有较好的定位效果.

图13 其他地形下的仿真结果Fig.13 Positioning results under other terrains

保持地形相关长度不变，改变地形均方根高度和地形地貌，发射天线位于地形较高处以保证可以

6 结 论

在构建场强地图时，山区的复杂地形给测试点位置信息的确定造成了极大的困难.本文提出了一种基于起伏地形与辐射电场分布相似性的定位方法，该方法通过对地理空间中电场分布规律的利用，尝试解决在山地地区构建场强地图时如何定位缺少坐标信息的场值测量区域的问题.通过对地形中不同位置、不同大小的模板区域、不同发射天线高度和不同地形地貌下的多角度仿真实验，充分显示了所提出的定位算法在山区地形环境中的有效性，具有较高的实际应用价值.下一步的重点工作是研究更加复杂地理环境(如不同传播媒介、多发射源情况等)的电场分布特性，以期得到适用性更广的定位算法.