高轨道目标电离层折射修正方法研究

刘琨 袁志刚 周晨 赵家奇 朱庆林 董翔 王海宁 盛冬生

（1.中国电波传播研究所，青岛 266107；2.武汉大学电子信息学院，武汉 430079）

引 言

电离层作为近地空间重要组成部分，当电波信号从中穿过时，电子密度及其不均匀分布使得电波信号传播速度变慢、路径发生弯曲，从而导致雷达等测控设备探测目标的距离、俯仰角、速度产生一定的偏差，即为折射误差[1].电离层是色散介质，对3.0 GHz以下频段电波信号影响最为显著，且频率越低影响越大[2]，电离层折射误差成为S及以下频段的导航、定位及测控等设备重要的误差源之一[3-7]，需要予以修正.需要说明的是，本文只研究和分析电离层距离折射误差修正方法，俯仰角和速度等折射误差的修正方法不作讨论.

为了消除电离层引起的卫星导航、雷达测控等系统测量误差，国内外多位学者提出了克罗布歇(Klobuchar)、NeQuick和国际参考电离层(internation reference ionosphere, IRI)等电离层模型以及观测数据同化电离层模型的方法等[8-15].陈学军等分析比较了Klobuchar模型、IRI模型和中国参考电离层模型航天器在外弹道测量中的修正精度[16]；美国夸家林导弹试验基地利用GPS计算电离层距离折射误差，用于P波段雷达折射误差修正[17]；李川川、刘琨给出了S频段雷达的电离层修正方法[18].上述研究基于电离层经验模型计算电离层距离折射误差，且忽略电离层水平不均匀性，可一定程度减小和修正电离层引起的折射误差.但由于模型构建未用或较少用到我国电离层观测数据，这使得在我国不同地区使用时，模型精度均受到一定影响，难以满足工程中越来越高测控精度的需要.

本文针对轨道高度大于2 000 km的高轨道目标高精度折射误差修正的需要，开展高精度折射误差修正新方法研究，给出了基于GNSS的空间投影法和自适应网格法两种电离层距离折射误差修正方法，并比较分析两种方法在不同仰角、角径时误差修正精度及适用性.

1 电离层距离折射误差修正方法

电离层距离折射误差主要包含延迟效应和弯曲效应，当目标仰角大于3°时，弯曲效应可忽略不计[18]，电离层距离折射误差即为电离层延迟.对于轨道高于2 000 km的目标而言，电波信号几乎穿过了全部电离层，电离层延迟 ∆R与电离层路径总电子含量(total electron content, TEC)存在着对应关系[19]：

由式(1)知，对于3°仰角以上的高轨道目标，高精度电离层距离折射误差关键在于获取目标路径电离层TEC，其计算方法可参考相关文献[20]，在此不再复述.

1.1 空间投影法

空间投影法如图1所示，在某一时刻t0，当目标与附近卫星之间的距离满足一定条件时，则认为目标到GNSS接收机的穿刺点(intersect pierce point,IPP)位置的垂直总电子含量(vertical TEC, VTEC)(记作 VTECIPPo)与观测卫星到接收机IPP点处的VTEC(记作 V TECIPPi)相等，即

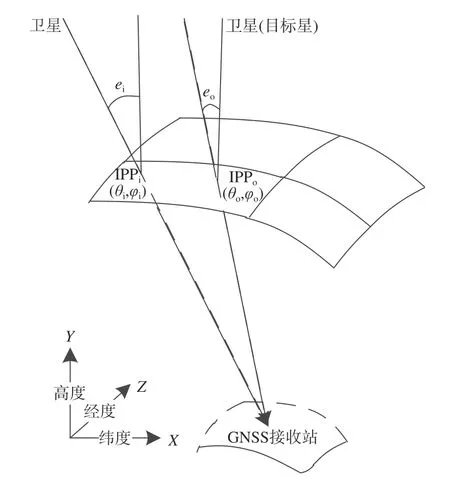
图1 空间投影法示意图Fig.1 Schematic diagram of space projection method

式中：θo、 θi表 示目标及卫星的经度； ϕo、 ϕi表示目标和卫星的纬度.目标及卫星的天顶角分别为eo、ei，由式(2)可得出：

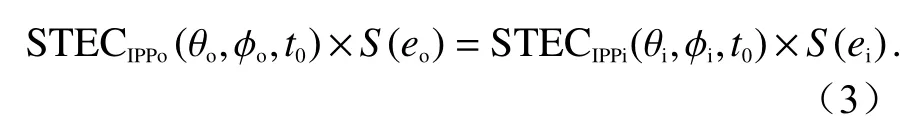
在空间投影法中，选择距离目标最近的卫星，即选择距目标角径最小的卫星，先计算其路径电子含量 S TECIPPi， 由式(3)计算对应路径电离层总电子含量 STECIPPo， 再由式(1)得到设备工作频率对应的电离层距离折射误差.

1.2 自适应网格法

在自适应网格法中，假设在一段时间(t0～ti)内卫星到接收机IPP点 VTECIPPi大小不变，随时间向西运动，运动位置用太阳时角S表示[20]，有

式中，时间t单位为小时.

角径相应地改写为

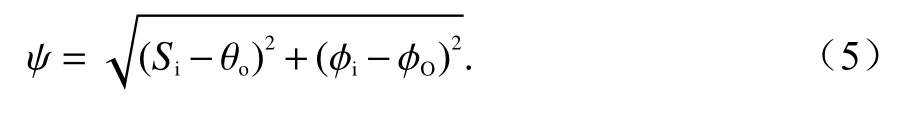
事实上，空间投影法将空间距离作为选择可用GNSS卫星的依据，即在某一时刻，选取的卫星与目标之间的角径最小.此时，角径 ψ为固定网格，仅与IPP点经纬度相关.在自适应网格法中，角径的划分考虑了电离层的地方时效应，将时间和IPP点的经度相互融合，以太阳时角替代经度，在一定时间范围内选取与目标时空角径最小的卫星.此时，角径则不再是固定的网格，而是融合时间信息的自适应网格.

2 不同方法修正精度分析与比较

利用国际GNSS服务组织(International GNSS Service, IGS)基准站TIDB站(−35.4°，148.9°)2016年年积日为25～27天的GPS数据，以卫星PRN7为目标星，分析和校验上述两种方法的电离层距离折射误差修正效果，结果如图2所示.先计算目标星PRN7对应路径电子含量，再转化距离折射误差修正量∆R0，并以此作为比较基准(假定设备的工作频率f0为2.0 GHz).空间投影法和自适应网格法所得到的电离层距离折射误差 ∆Rmap、 ∆Rada分别用蓝色线和红色线表示， ∆RLi(黑色线)是文献[18]方法计算结果.IRI模型及其他常用方法修正精度均低于上述方法，在此不再给出.可以看出：在高仰角处，距离折射误差 ∆Rmap、 ∆Rada与真实值 ∆R0具有较好的一致性；而在低仰角处，文献[18]方法和空间投影法计算误差较大.这表明：在高仰角时，上述方法修正精度均较理想；而低仰角，只有自适应网格法修正效果较为理想，其他两种方法则修正精度有所降低.

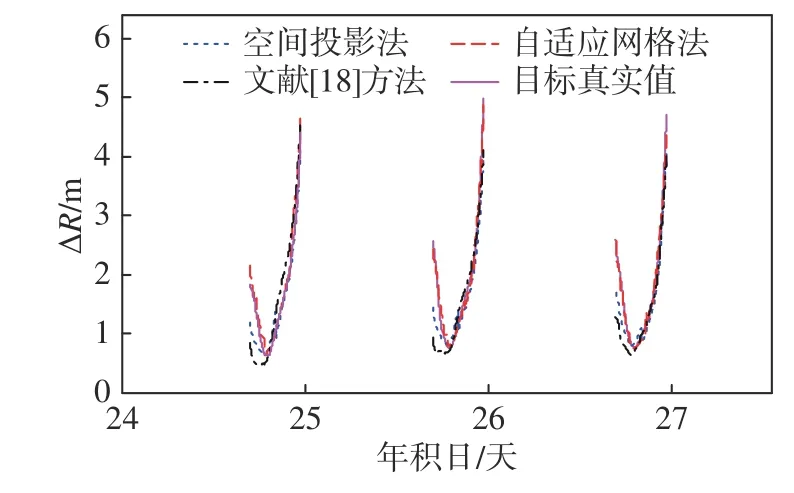
图2 自适应网格法和空间投影法修正效果一致性分析Fig.2 Analysis of the consistency between adaptive mesh method and space projection method

相应地，图3分别给出空间投影法、自适应网格法和文献[18]方法计算的距离折射误差修正剩余∇Rmap(蓝色线)、 ∇Rada( 红色线)和 ∇RLi(黑色线)，其中：∇Rmap=∆Rmap−∆R0； ∇RLi=∆RLi−∆R0； ∇Rada=∆Rada−∆R0.可以看出：在仰角大于45°的高仰角处，空间投影法和自适应网格法修正精度较高，修正剩余 ∇RLi、∇Rada、 ∇Rmap较小，一般小于0.2 m；随着仰角的降低，文献[18]方法和空间投影法修正剩余则快速增大，修正精度快速降低恶化，而自适应网格法修正剩余则几乎不受仰角变化的影响，且比其他两种方法的修正剩余均小得多.

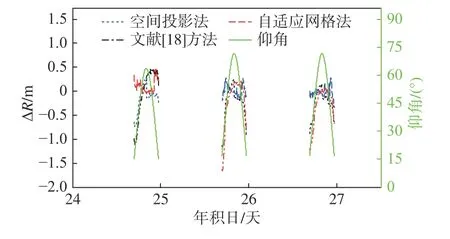
图3 自适应网格法和空间投影法修正剩余残差分析Fig.3 Residual error analysis of adaptive mesh method and space projection method

为了进一步分析空间投影法和自适应网格法电离层误差修正效果，图4给出了两种方法修正剩余∇Rmap、∇Rada随目标仰角变化情况.可以看出：文献[18]方法修正剩余随着仰角降低快速增大，在15°仰角时，修正剩余甚至超过1.5 m，误差修正精度不够理想；相比较而言，空间投影法修正剩余在低仰角有所改进，但修正剩余也达到1.0 m，该方法在低仰角处修正精度有待进一步提高；自适应网格法修正剩余一般小于0.2 m，且与目标仰角大小几乎无关，电离层距离折射误差得到有效修正.上述结果表明，自适应网格法修正精度较高，且不受目标仰角大小的影响，较好地满足了低仰角时高轨道目标高精度折射修正的需要，具有较高的工程应用价值.

图4 自适应网格法和空间投影法修正剩余随仰角分布Fig.4 Correcting residual distribution with elevation angle of adaptive mesh method and space projection method

表1给出上述三种距离折射误差修正方法的统计分析.自适应网格法距离折射误差修正剩余的均值和均方根分别为0.03 m和0.13 m，较其他两种方法的修正剩余更小，修正精度更高.

表1 不同距离折射误差修正方法统计分析Tab.1 Statistical analysis of refraction error correction methods at different distances

将其余GPS卫星依次作为目标星，统计分析空间投影法和自适应网格法电离层距离折射误差修正精度，如图5所示.可以看出，对于所有GPS卫星而言，自适应网格法误差修正剩余 ∇Rada均明显小于空间投影法的修正剩余 ∇Rmap，这进一步表明了自适应网格法具有更高的修正精度，对所有卫星普适性更强，且不受目标仰角大小的影响.即自适应网格法具有更高的修正精度和适用性，建议在深空及高轨目标测控等工程中可优先考虑选用自适应网格法进行电离层距离折射误差修正.

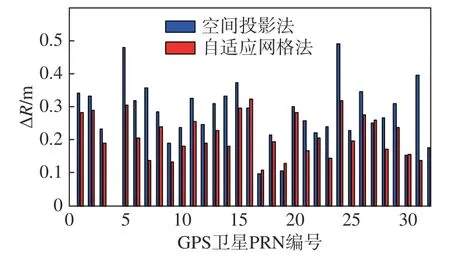
图5 自适应网格法和空间投影法修正普适性统计效果分析Fig.5 Analysis of the statistical result of adaptive grid method and space projection method

3 结 论

本文针对高分、探月、火星探测等重大项目的高精度电离层距离折射误差修正的需要，提出了适用于轨道高于2 000 km目标的空间投影法和自适应网格法，并比较分析了两种方法的修正精度及不同仰角、角径时的适用性.结果表明：对于2.0 GHz电波信号而言，在大于45°的高仰角处，空间投影法和自适应网格法距离折射误差修正精度较高，修正剩余小于0.2 m；在低仰角时，空间投影法修正精度快速降低恶化，距离折射误差修正剩余大于0.5 m，有时甚至达到1 m量级，而自适应网格法修正剩余不受目标仰角大小影响，即自适应网格法较时空投影法修正精度更高，适用性强，特别在低仰角处，自适应网格法优势更为显著.

另外分析表明，当选用的卫星距离目标越近，角径越小时，空投影法和自适应网格法距离折射修正精度就越高.需要指出的是，本文仅用到GPS卫星数据进行误差计算，为了确保每个时刻GPS数据可用性，采用距离目标星最近、角径最小的卫星.事实上，由于 GPS数据有限，某些时刻所选用的卫星距离目标星较远、角径较大，这一定程度上影响了电离层距离折射误差修正精度.随着GNSS系统建设和完善，特别是我国北斗系统全面建成，在视卫星超过30颗，可用于折射误差修正的GNSS卫星数量将越来越多，可用的GNSS卫星角径也将大为减小，这意味着电离层距离折射修正精度可得到进一步的改进和提高.