五轴联动加工速度前瞻时变周期规划

曹宇钊，彭宝营，王增新

(1.北京信息科技大学 机电工程学院,北京 100192;2.超同步股份有限公司，北京 101500)

0 引言

目前数控系统已经得到较快速的发展，为高效地获得高精度加工零件，国内外研究者已越来越重视数控系统在刀具进给速度控制方面功能的开发和研究工作[1]。数控机床的进给速度规划不仅直接影响加工的精度、速度以及零件表面的光洁度，而且还与刀具和机床的稳定性和使用寿命密切相关[2]。

王云凯[3]从进给速度的角度出发提出了弓高误差进给速度自适应非均匀有理B样条曲线即NURBS(non-uniform rational B-splines)插补算法。唐清春等[4]推导出叶片五轴端铣和侧铣时的进给速度补偿算法。周玉龙[5]分析了五轴加工中的非线性误差，用刀具路径中点处的误差近似求解非线性误差。谢斌等[6]基于控制弦误差的插补算法，提出了一种自适应速度控制的智能算法。B.Gassara等[7]建立速率模型对插补速率进行评估。Firman Ridman等[8]通过对速度进行优化，大大缩短了加工时间。P.Gray[9]及Xavier Beudaert等[10]对刀具路径进行平滑处理，实现了线性插值和非均匀有理样条插补。周瑞红等[11]基于Pro/E通用软件平台，提出了进给速度控制方法，提高了加工效率。赵国勇等[12]利用跃度连续的加减速方法，获得更平滑的速度轮廓运动曲线，且更具柔性。Yong等[13]综合考虑弓高误差以及刀具运动的加减速约束，提出了一种离线的自适应速度规划方法，提高了机床运动的平稳性。

以上研究成果采用对五轴加工过程中速度的控制来实现零件表面质量的提高，但速度控制均是局部区域或者是特殊点组成的部位，并且计算涉及多个参数，过程相当复杂，效率不高。本文对时变周期进行规划，从改变进给周期的角度来对速度和加速度进行控制。该方法无须预测加减速点，且计算量少，速度与加速度均在限定值以内，能够提高机床加工的稳定性。

1 B-C摆头转台RTCP运动学模型

在五轴加工系统中，由于运动学正逆解的存在，会导致系统控制点与实际运动位置不匹配。旋转刀具中心点(rotational tool center point，RTCP)可以有效解决这个问题。当编程轨迹已知时，B轴或C轴转动一定的角度后，为维持刀尖点沿已知轨迹运动，需要调整线性轴的位置，对旋转轴中心位置进行补偿，旋转轴中心补偿位置计算的过程，即为旋转刀具中心点RTCP。

B-C摆头转台RTCP原理如图1所示。在刀具坐标系O2中，设定初始状态刀位点为P0(0，0，0)，刀轴矢量为U0(0，0，L)，L为刀具坐标原点到回转轴交点的距离，机床平动轴初始状态为PM(PMX,PMY,PMZ)，B、C摆动的角度分别是β、γ。在工件坐标系O3中，刀位点矢量和刀轴方向矢量分别为P(PX,PY,PZ,)和U(UX,UY,UZ)。其中，PX、PY、PZ分别为刀尖在X、Y、Z三个方向的坐标，UX、UY、UZ分别为刀轴姿态在X、Y、Z三个方向的矢量投影。

图1 B-C摆头转台RTCP原理

其中刀位点矢量P和刀轴方向矢量U可由P0、U0先平移PM的距离到工件坐标系上，然后再分别绕B轴、C轴旋转β、γ的角度，最后再平移-PM的距离变换到刀具中心坐标系。可列出以下变换矩阵：

(1)

(2)

式中：T为平动进给轴单位矩阵；R为转动进给轴单位矩阵。其中：

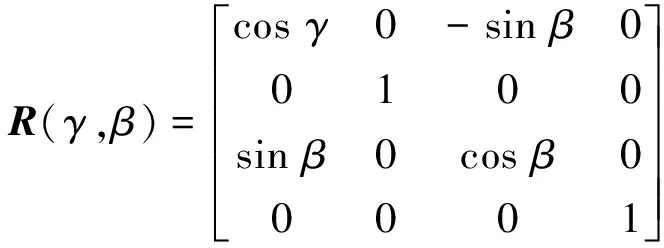
由式(1)、(2)可以推导出机床的正运动学变换公式：

(3)

(4)

根据式(3)、(4)可以推导出机床的逆运动学公式：

(5)

2 五轴联动加工速度与加速度前瞻控制

2.1 五轴联动加工速度与加速度超限分析

五轴联动加工过程中，控制五轴矢量速度时，每组指令点间的时间间隔T0可根据编程坐标与编程速度的比值计算，如式(6)所示。其中，F为编程速度，μX、μY、μZ、μB、μC为长度或角度的标准单位转换为脉冲值的数量值[14]。

(6)

RTCP逆解位置除以时间间隔T0得到各轴的速度：

(7)

五轴联动加工速度为各轴速度的矢量和，计算如式(8)所示：

(8)

各轴速度差除以时间间隔可以得到各轴加速度：

(9)

各轴的矢量和的计算如式(10)所示：

(10)

实际的加工加速度为

(11)

由式(7)速度求解公式可知，时间间隔是由运动学正解位置除以编程速度所得，而各轴速度是由运动学逆解位置除以时间间隔所得，这导致了线性轴速度超过了最大速度限制。加速度由速度差除以时间间隔所得，这导致了线性轴加速度大大超过了最大加速度限制。而速度和加速度超限会影响加工稳定性，从而影响加工精度。

2.2 约束条件下的速度计算

对于实际加工过程中速度超限的情况，我们可以先对速度进行约束。以弓高误差约束和向心加速度约束为条件，可以计算出最大许用速度。然后对其进给周期进行调整，找到最适合的进给周期，使其满足最大限度的速度与加速度。

2.2.1 弓高误差约束的进给速度

曲线的弓高误差

(12)

式中：v为给定进给速度；ρ为插补点处对应的曲率半径；T1为插补周期。设定最大弓高误差δlim，可求得进给速度：

(13)

2.2.2 向心加速度约束的进给速度

曲线运动的向心加速度

(14)

式中：v0为给定的进给速度；ρ为插补点处对应的曲率半径。则向心加速度约束下的进给许用速度

(15)

式中ar,lim为设定的向心加速度极限值。限定的最大进给速度

Vk=min(V(ρ),Va(ρ))

(16)

2.3 五轴联动成形速度控制策略

由2.1节五轴联动加工速度与加速度超限分析，为了使各轴速度限制在允许范围内，可以改变进给周期来避免超限。如式(17)所示，当增大时间间隔时，各轴的速度会减小，同理加速度也会减小。

(17)

所以，可以通过实时地增大进给周期来对速度和加速度进行前瞻约束，避免其超限。由式(16)计算出最大进给速度，由式(9)计算出加速度，再对速度和加速度分别判定是否超限，对超限的做周期规划，增大时间间隔，最终可以得到整个时变进给周期。时变进给周期规划流程如图2所示。

图2 时变周期规划流程

按照上述的规划流程可以得到实时的进给周期。通过增大到合适的进给周期，规划出在限定之内的速度与加速度，可以保证加工过程的稳定性。

3 仿真实验

“S”试件是五轴加工的典型零件，本次试验加工采用的也是“S”试件。首先用UG进行“S”件的三维建模，然后将试件模型导入到CAM软件进行路径规划，生成NC代码。提取其中300个加工点的轨迹图如图3所示，旋转轴如图4所示。

图3 直线轴加工点路径

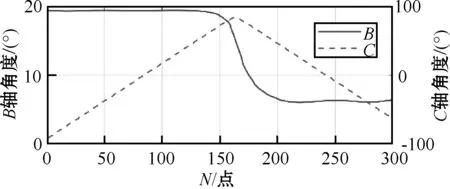
图4 BC轴加工点路径

设定编程速度为500 mm/s,最大加速度为2 000 mm/s2，由式(5)可以求出电机轴的位置，根据式(7)、(9)求解各个轴的速度、加速度。根据式(6)可以求出时间周期如图5所示。

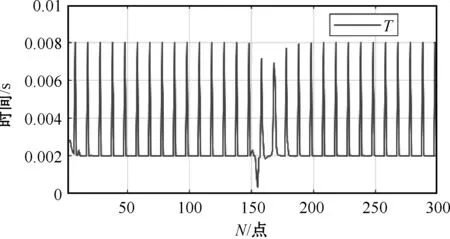
图5 时间周期计算

各轴速度求解如图6、7所示。

图6 直线轴速度计算

图7 旋转轴速度计算

根据式(8)计算出矢量速度和为1 231.98 mm/s,而编程速度是500 mm/s，加工速度是编程速度的2.46倍。各轴加速度求解如图8、9所示。

图8 直线轴加速度计算

由图9可知矢量加速度也已经远远大于最大限定值。为了满足限定加速度最大值的要求，现对周期进行调整。由式(16)可求最大速度限制为1 500 mm/s，设定最大加速度为2 000 mm/s2，则按照图2时变周期原理可求出进给周期如图10所示。

图9 旋转轴加速度计算

图10 时变周期

其中最大时间间隔为0.028 46 s。原时间周期最大时间间隔为0.008 s。与原来的时间间隔相比，时变周期增大了时间间隔。按照上图时变周期可以分别求出各轴速度，如图11、12所示。

图11 时变周期直线轴速度计算

图12 时变周期旋转轴速度计算

由图11、12可知，各轴加工速度没有超过限定值，矢量和最大值为643.35 mm/s，没有超过速度设定值。五轴联动加工各轴加速度如图13、14所示。

图13 时变周期直线轴加速度计算

图14 时变周期旋转轴加速度计算

由图13、14可知，计算得出的各轴加速度均在最大限度范围之内，计算出各轴矢量和最大值为1 957.23 mm/s2，小于设定值，满足要求。

4 结束语

由速度超限分析可以知道，在实际加工过程中，必然会出现速度和加速度超限的情况，因此本文提出了时变周期的规划。对速度与加速度超限的位置进行时间间隔的增大调整，使其满足加工过程中速度与加速度在最大限制范围之内的条件。实验仿真结果表明，进给周期规划后，速度和加速度均在限定范围之内，对进给周期的调整减少了对数控机床的冲击，提高了加工的稳定性。