基于多粒度概率粗糙集与MULTIMOORA的q-RO模糊多属性群决策
白文慧,张 超,2,陈炜哲,李德玉,2,上官学奎,马瑾男
(1.山西大学 计算机与信息技术学院,太原 030006;2.计算智能与中文信息处理教育部重点实验室(山西大学),太原 030006;3.山西省信息产业技术研究院有限公司,太原 030012)
0 引 言
当前,许多复杂决策问题的高效求解涉及相互联系或相互制约的属性,需要决策者针对有限个方案从多个属性的视角进行分析并选择最优方案,从而形成了多属性决策[1-2]。此外,在许多重要决策过程中,为了体现科学化与民主化,通常要求一个群体来参与决策,该群体通过商议、协调或谈判来得出决策结论,这类由多个决策者参与的形式即为群决策[3]。多属性群决策是多属性决策与群决策的交叉研究方向,结合多个决策者给出的方案偏好信息,将其集成为群体偏好信息,并利用所构建的理论对各方案进行择优[4]。近年来,多属性群决策已成为现代决策领域的研究热点,有力推动了社会经济的快速发展。
q-RO模糊集由Yager[5]首先提出,该类模糊集由隶属度μ与非隶属度ν构成,且满足μq+νq≤1。此外,当q=1时,q-RO模糊集退化为直觉模糊集[6];当q=2时,q-RO模糊集退化为勾股模糊集[7]。显然,q-RO模糊集为直觉模糊集与勾股模糊集的拓展形式。例如,某决策者针对一个备选方案在某一属性下的评估值为(0.7,0.8),不难发现0.7+0.8=1.5>1,0.72+0.82=1.13>1,0.73+0.83=0.855<1成立。因此,直觉模糊集与勾股模糊集无法有效表示上述评估值,但q-RO模糊集的引入扩大了决策信息的表示范围,可合理描述评估值(0.7,0.8)。学者们考虑到q-RO模糊集在信息表示范围方面的优势,逐渐关注并发展了q-RO模糊多属性群决策问题,并取得了丰硕的研究成果[8-10]。
在决策信息融合与分析中,多粒度概率粗糙集可同时体现多粒度粗糙集[11-12]与概率粗糙集[13-14]的特点和优势。一方面,在乐观、悲观、可调节等不同多粒度计算模型[15-17]的支持下,多粒度粗糙集可用于高效求解风险型多属性群决策问题;另一方面,在经典粗糙集中,粗糙近似的结构比较严格且缺乏容错能力,概率粗糙集通过引入阈值使其具备了容错能力,学者们在此基础上系统探索了基于概率粗糙集的多类理论模型。近年来,多粒度概率粗糙集已应用于许多实际应用领域,如双边匹配[18]、分类模型[19]、属性约简[20]等。
Brauers[21]指出,结合多种决策方式的多属性决策方法所得结果优于仅使用某一类决策方式的多属性决策。故Brauers和Zavadskas[22]将全乘模型引入比例分析多目标优化(multi-objective optimization by ratio analysis, MOORA)中,提出了全乘比例分析多目标优化(MOORA plus the full multiplicative form, MULTIMOORA)。总体来看,MULTIMOORA因其运算简单、鲁棒性强等优点,已逐渐引起了各领域研究人员的广泛关注[23-25]。
本文为探索q-RO模糊信息系统中具备稳定决策结果的多属性群决策方法,依据多粒度概率粗糙集与MULTIMOORA建立q-RO模糊多属性群决策方法,为获得稳定决策结果提供模型与方法方面的理论支撑。本文的主要贡献包括3方面:①提出了多粒度q-RO模糊概率粗糙集模型;②建立了基于多粒度q-RO模糊概率粗糙集与MULTIMOORA的q-RO模糊多属性群决策方法;③通过实例分析和对比性分析验证了所建立方法的可行性与有效性。
1 基本理论
1.1 q-RO模糊集
定义1[5]设U是一个非空有限论域,论域U上的一个q-RO模糊集表示为
B={〈x,(μb(x),νb(x))〉|x∈U}
(1)
(1)式中:函数μb:U→[0,1]和νb:U→[0,1]分别表示q-RO模糊集B的隶属度和非隶属度。对于任意x∈U,满足(μb(x))q+(νb(x))q≤1,q≥1。此外,将q-RO模糊数记作b=(μ,ν)。
在q-RO模糊多属性群决策中,q-RO模糊数的比较机制起着关键作用,其得分函数和精确函数的定义如下。
定义2[8]令b=(μ,ν)为一个q-RO模糊数,b的得分函数和精确函数表示为
(2)
(3)
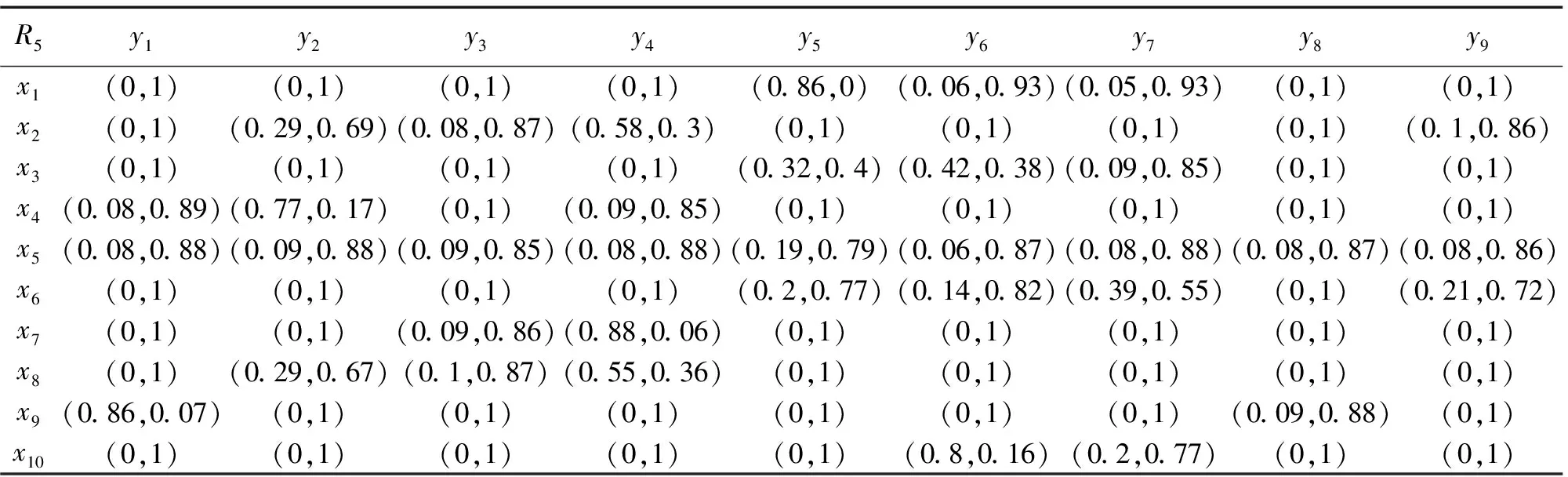
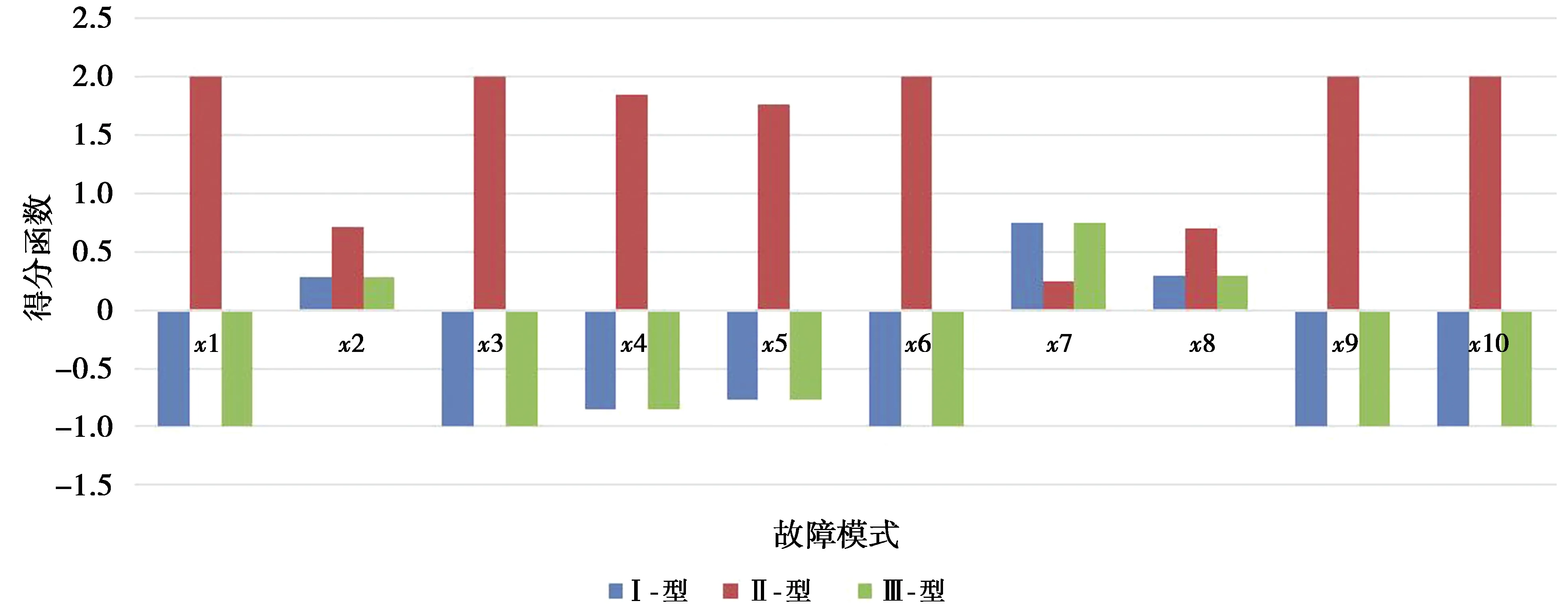
对于2个q-RO模糊数b和b′,若s(b)>s(b′),则b>b′;若s(b) 定义3[7,18]令b=(μ,ν)和b′=(μ′,ν′)为2个q-RO模糊数,存在如下主要运算规则。 6)bb′= 定义4[18]设U和V是2个非空有限论域,U×V上的q-RO模糊关系R表示为 R={〈(x,y),μR(x,y),νR(x,y)〉| (x,y)∈U×V} (4) (4)式中:μR(x,y)和νR(x,y)取值为[0,1],代表(x,y)对R的隶属度和非隶属度。对于任意(x,y)∈U×V,令γ∈μR(x,y),η∈νR(x,y),γ+=max{γ|γ∈μR(x,y)}和η+=max{η|η∈νR(x,y)},则有0≤γ,η≤1且0≤γ+,η+≤1。 定义5[13]令U,R,P分别代表一个非空有限论域,该论域上的等价关系和概率度量,称(U,R,P)为一个概率近似空间。对于任意x∈U和阈值0≤β<α≤1,X的上下近似定义为 (5) (6) MULTIMOORA是Brauers和Zavadskas[22]建立的一种具备稳定决策结果的方法,通常包括比率系统、参考点、全乘法形式。其中,在比率系统中,xij代表目标i(i=1,2,…,n)上备选方案j(j=1,2,…,m)的对应值。将一个目标对备选方案的每个对应值作为分子,该目标有关的所有备选方案的平方和的平方根作为分母,即 (7) (8) 参考点是求参考点与对应点的最小最大度量,即 (9) 与其他决策方法相比,MULTIMOORA主要有以下优点:①通过结合多个基本方法,使得所求结果准确性更高;②能有效解决具有多个备选方案的复杂多属性决策问题;③计算过程易于理解,运算速度快。 在q-RO模糊信息系统中,q可取满足对于任意x∈U,(μb(x))q+(νb(x))q≤1,q≥1的任意值。一般情况下为了运算方便,取满足条件的最小q值。 本节在q-RO模糊信息系统中,结合多粒度粗糙集与概率粗糙集,提出3类多粒度q-RO模糊概率粗糙集模型。 1)Ⅰ-型多粒度q-RO模糊概率粗糙集。本节采用加权平均算子来构建Ⅰ-型多粒度q-RO模糊概率粗糙集,可克服乐观、悲观多粒度概率粗糙集存在信息融合极端性方面的局限。 (10) 2)Ⅱ-型多粒度q-RO模糊概率粗糙集。距离度量是q-RO模糊信息融合过程中的关键步骤,本节采用欧氏距离法构建Ⅱ-型多粒度q-RO模糊概率粗糙集。 (11) 3)Ⅲ-型多粒度q-RO模糊概率粗糙集。加权平均算子倾向于考虑评价集中的群体性意见。本节依据加权几何算子构建Ⅲ-型多粒度q-RO模糊概率粗糙集,该方法倾向于考虑评价集中的个体意见。 (12) 给定一个q-RO模糊信息系统(U,V,Ri,B),首先利用离差最大化法[26]求出每个属性的权重值和每个决策者的权重值。 令 (13) (14) (15) (16) 对于任意xj∈U,yk∈V,xj关于信息系统(U,V,Ri,B)的多粒度隶属度为 (17) 排序函数Ind(xj)(j=1,2,…,p)表示xj的值在所有x的值中从大到小的排序值。如设x1=0.4,x2=0.8,x3=0.6,则Ind(x1)=3,Ind(x2)=1,Ind(x3)=2。 输入:一个q-RO模糊信息系统(U,V,Ri,B)。 输出:最佳备选方案x*。 步骤1选取合适的q值; 步骤2计算每个属性的权重值和每个决策者的权重值; 步骤5根据排序函数Ind(ξj),Ind(ψj),Ind(ζj),得到MULTIMOORA排序; 算法流程图如图1。 图1 q-RO模糊多属性群决策流程图 在模型算法中,步骤1选取q值的复杂度为O(pn);步骤2计算各个属性权重值的复杂度为O(p2m),各决策者权重值的复杂度为O(p2n);步骤3计算隶属度θ的复杂度为O(pmn);步骤4计算得到3种排序的复杂度为O(m2);步骤5—步骤6选择最佳备选方案的复杂度为O(p)。因此,该算法的总体时间复杂度为O(p2n)。 本节以文献[18]中的案例为背景进行实例分析,给出q-RO模糊多属性群决策的具体步骤。 假设某投资公司拟从财务指标的视角出发,选择一个符合公司合作意向、要求和战略地位的商业伙伴。为体现科学化与民主化,由3位财务专家构建了一个q-RO模糊信息系统(U,V,Ri,B)(i=1,2,3)。首先,令U={x1,x2,x3,x4}为经考察后可选企业的集合,V={y1,y2,y3,y4,y5}为企业财务指标的集合,其中,yk(k=1,2,3,4,5)分别表示毛利率、流动比率、应付账款周转率、资产负债率、净资产收益率。3位财务专家根据论域U和论域V给出的q-RO模糊关系如表1—表3。标准财务指标为B={ 表1 备选企业财务指标的q-RO模糊关系1 表2 备选企业财务指标的q-RO模糊关系2 表3 备选企业财务指标的q-RO模糊关系3 首先,根据(U,V,Ri,B)中所有评估值,确定本实例中q的最小值为3。 因此,可得Ⅰ-型排序结果ξ3>ξ4>ξ2>ξ1。 因此,可得Ⅱ-型排序结果ψ3>ψ4>ψ2>ψ1。 然后,可计算出下列多粒度q-RO模糊隶属度为 因此,可得Ⅲ-型排序结果ζ3>ζ4>ζ2>ζ1。 根据以上3种不同企业的排序,确定以下排序函数。 Ind(ξ3)=Ind(ψ3)=Ind(ζ3)=1; Ind(ξ4)=Ind(ψ4)=Ind(ζ4)=2; Ind(ξ2)=Ind(ψ2)=Ind(ζ2)=3; Ind(ξ1)=Ind(ψ1)=Ind(ζ1)=4。 最后,依据本文所建立的q-RO模糊多属性群决策方法,可得排序结果x3>x4>x2>x1,即最佳企业为x3。 灵敏度分析是一种常见的分析不确定性的实验方法,其实质是通过逐一改变相关变量的数值来解释关键指标受这些因素变动影响大小的规律。 本文通过改变上述实例中的q值来观察决策结果的变化。当q的取值为5时,计算结果如表4,排序结果为x3>x4>x2>x1。 表4 q=5时,q-RO模糊多属性群决策结果 当q的取值为10时,计算结果如表5,排序结果为x3>x2>x4>x1。 表5 q=10时,q-RO模糊多属性群决策结果 当q的取值为20时,计算结果如表6,排序结果为x3>x2>x4>x1。 表6 q=20时,q-RO模糊多属性群决策结果 结果表明,当q发生变化时,排序结果和之前有一些差别,但不影响最终的结果,最优企业仍为x3。因此,本文所建立的q-RO模糊多属性群决策方法在上述实例中具备稳定性。 Wang和Triantaphyllou[27]提出了多属性决策方法有效性测试的标准。本节通过测试1和测试2证明所建立的q-RO模糊集多属性群决策方法具备有效性。 测试1在一个有效的多属性群决策分析中,用一个更差的备选方案去替代非最优方案时不会改变最优备选方案。在上述实例中,分别用表1—表3中x4的补集替代x1,计算结果如表7。 表7 q-RO模糊多属性群决策测试1结果 排序结果为x3>x4>x2>x1,最佳选项为x3。该结果与4.1节中的结果一致。因此,测试1验证了本文所建立的多属性群决策方法具备有效性。 测试2若将一个多属性群决策问题分解成若干小规模决策问题,分别对它们使用相同的决策方法,将结果进行组合后,最后结果应与原结果保持一致。在上述实例中,若将决策问题分成2个小规模的多属性群决策问题,即{x1,x2,x3}和{x2,x3,x4},然后采用本文所建立的方法可得x3>x2>x1和x3>x4>x2,进行组合之后,该结果与原结果保持一致。因此,测试2验证了所建立的多属性群决策方法具备有效性。 本节将分别用上述提到的3种多属性群决策方法以及决策指标集的方法与本文中的可调多粒度多属性群决策方法进行了对比性分析。 分析1比较了上文提到的3种决策方法以及本文提出的可调多粒度多属性群决策方法,结果如图2。 图2 文献[18]背景下4种多属性群决策方法结果对比 从图2中可看出,不同方法所得计算结果虽存在差异,但这4种方法选择出的最优备选企业均为x3。 分析2使用基于指标集的决策方法,计算结果如下。 计算结果显示T1∩T2∩T3={3}≠∅,因此,最优备选企业仍为x3。 整体来看,本文所建立的q-RO模糊多属性群决策方法利用了MULTIMOORA的优势,并克服使用单一决策方法所带来决策结果存在差异的局限,可为获取稳定决策结果提供理论支撑。 本节以文献[28]中案例为背景,进行如下实验分析。 在蒸汽轮机的故障诊断过程中,假设1组10个故障模式表示为U={x1,x2,…,x10},其中,xj(j=1,2,…,10)代表不平衡、气动力耦合、偏移中心、油膜振荡、转子的径向冲击摩擦、共生松动、抗静电轴承损伤、喘振、轴承块松动、非均匀轴承刚度。另一论域V={y1,y2,…,y9}代表9个频率范围,其中,yk(k=1,2,…,9)表示不同频谱的一些频率范围:C1(0.01-0.39f),C2(0.4-0.49f),C3(0.5f),C4(0.51-0.99f),C5(f),C6(2f),C7(3-5f),C8(f的奇数倍),C9(大于5f的高频),故障测试的样本为D。为解决该多属性群决策问题,每位机械工程师都提供他们关于系统故障的决策偏好,如表8—表10,并以q-RO模糊集的形式给出。D={ 表8 工程师1提供的系统故障知识 表9 工程师2提供的系统故障知识 表10 工程师3提供的系统故障知识 通过本文所建立的算法进行决策分析,计算结果如表11和图3。不难看出,最终排序结果显示最优备选项为x7,与文献[28]结果一致,因此,进一步验证了本文所提出方法的有效性。 表11 实例2的计算结果 图3 文献[28]背景下4种多属性群决策方法结果对比 本文针对q-RO模糊多属性群决策问题,首先提出了3类多粒度q-RO模糊概率粗糙集。然后,建立了基于多粒度概率粗糙集与MULTIMOORA的q-RO模糊多属性群决策方法。最后,通过实际算例验证了所建立方法的可行性与有效性。在接下来的研究中,有必要进一步探索大规模群体决策、动态决策等问题,并利用更广泛的知识发现工具来获得更具说服力和可解释性的决策结论。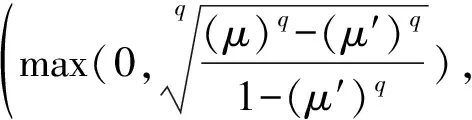
1.2 q-RO模糊概率粗糙集

1.3 MULTIMOORA

2 多粒度q-RO模糊概率粗糙集



3 基于多粒度概率粗糙集与MULTI-MOORA的q-RO模糊多属性群决策
3.1 模型建立



3.2 模型算法



3.3 算法复杂度
4 实例分析
4.1 实例描述



4.2 决策过程


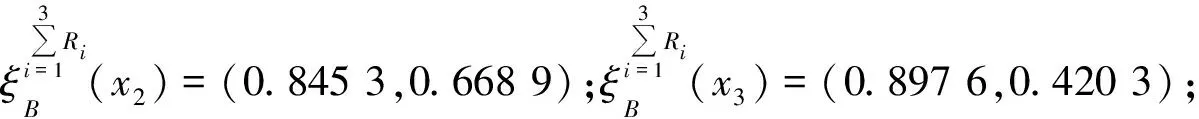
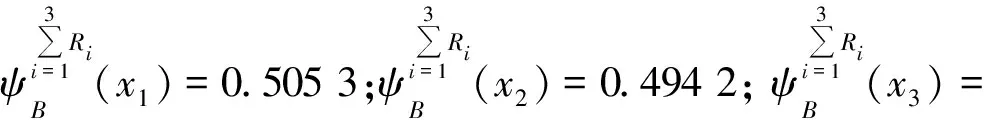

4.3 灵敏度分析
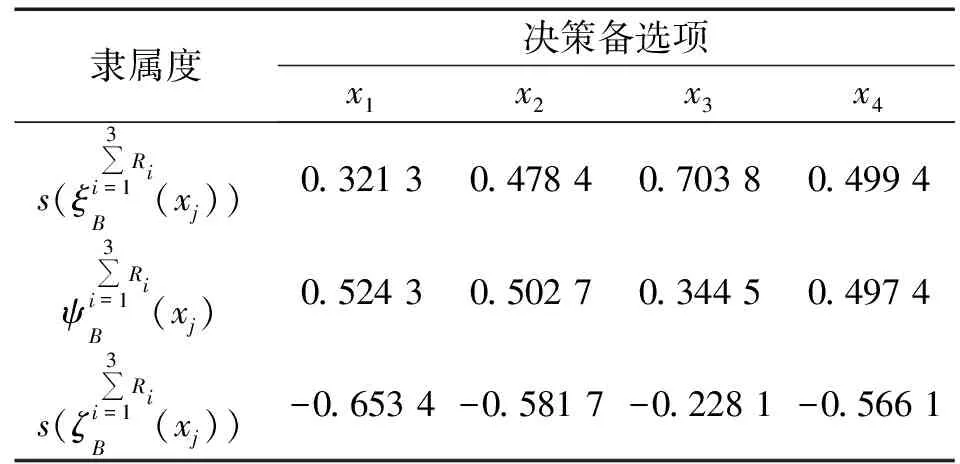
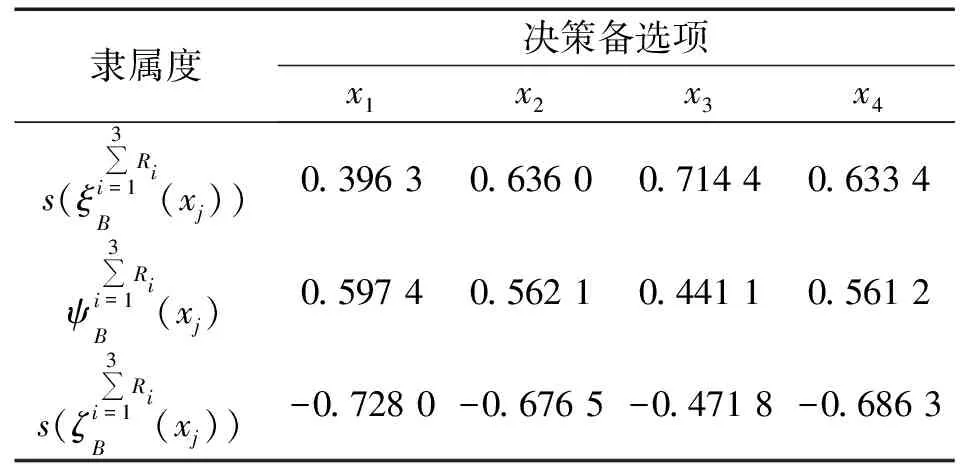

4.4 有效性测试

4.5 对比性分析

4.6 实验分析



5 总 结

