摩擦力矩特性对卫星跟踪转台运动性能的影响研究

郑文颖, 许吉敏, 王 伟

(合肥工业大学 机械工程学院,安徽 合肥 230009)

搭载在侦查卫星等移动平台上的光电跟踪转台是实现对空间和地面目标捕捉、跟踪的核心装备。提高卫星跟踪转台的运动精度对升级我国国防、民用监测系统有重要的战略价值,在国务院颁发的《中国制造2025》产业规划中也提到要重点发展新型卫星等空间平台与有效载荷。目前跟踪转台的轴系普遍采用滚动轴承作为主支撑部件,其摩擦力矩特性是影响转台运动性能的最重要因素[1]。虽然卫星跟踪转台长期工作于太空微重力环境中,但其安装调试都是在地面上进行的,地面模拟试验与在轨运行实况之间存在较大误差。究其实质,在轨运行转台的摩擦力矩特性不同于地面环境,以摩擦力矩为纽带的卫星跟踪转台地面模拟试验方案才是解决上述较大误差问题的关键[2]。因此研究摩擦力矩特性对转台运动性能的影响不仅有助于转台精度的增长,同时可为地面模拟试验方案提供理论参考。

为提高卫星跟踪转台的运动精度,研究人员从摩擦补偿、控制方法、支撑部件优化设计等角度开展了大量研究。摩擦补偿分为基于摩擦模型和基于非模型2种方法。非模型补偿大多使用传统的比例积分微分(proportional integral differential,PID)控制,需采用鲁棒控制器来避免极限环振荡;基于摩擦模型的补偿方法应用广泛,具体原理为根据所选摩擦模型得到一个补偿量,然后施加到控制系统中以抵消每一瞬时的摩擦力矩,其实质为一种前馈控制方法。在模型补偿的控制方法中,摩擦模型的选择是关键,这是由于摩擦模型决定了摩擦动静态特性的表征形式,库仑摩擦模型、LuGre摩擦模型、Stribeck摩擦模型等都是常用的摩擦模型[3]。在控制方法方面,模糊控制算法与经典PID控制器相结合,形成的模糊PID控制器实现了单轴转台的高精度控制[4-5]。反向传播(back propagation,BP)神经网络PID和径向基函数(radial basis function,RBF)神经网络滑摩变结构控制方法与传统PID相比具有一定的优越性[6]。此外,基于内模原理的重复控制理论与传统超前校正相结合的复合控制方法在提高跟踪转台精度方面也取得了显著成果[7-11]。在支撑部件优化设计方面,研究者主要通过引入高弹性模量厚涂层或更换新类型轴承使得支撑部件的摩擦力矩数值小而平稳,从而改善伺服控制精度,如采用低温高速火焰喷涂工艺在轴承滚道上制备WC-12Co厚涂层、采用超导磁悬浮轴承等[2,12]。

本文以二轴卫星跟踪转台中支持整体框架运转的方位轴为研究对象建立机电动力学模型。采用基于摩擦模型的补偿控制方法分析库仑摩擦模型和LuGre摩擦模型的伺服控制效果,重点比较不同运动频率下的角位置和角速度跟随特性,研究摩擦力矩数值变化下的卫星跟踪转台运动性能。相关理论研究对卫星跟踪转台精度增长、地面模拟试验等方面的工作有理论价值。

1 方位轴机电动力学模型

二轴卫星跟踪转台由相互垂直的方位轴和俯仰轴组成,是一种最常见的转台结构,其示意图如图1所示。在轴端的伺服电机驱动下,两轴联动实现有效载荷(如红外相机)2个自由度的运动,从而实现对目标的捕捉和跟踪;俯仰轴实现有效载荷绕水平轴的俯仰运动;方位轴实现整个转台框架的回转运动,其支撑轴承载荷远大于俯仰轴,是转台中最重要的部分。本文以某型二轴卫星跟踪转台中的方位轴为对象,研究摩擦力矩特性对其运动性能的影响。

图1 二轴卫星跟踪转台的结构示意图

方位轴的伺服电机电路方程和动力学方程为:

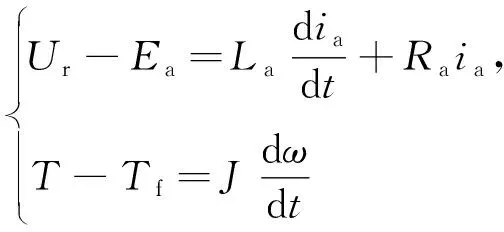
(1)

其中:Ur为电枢控制输入电动势;Ea为反电动势;La为电感;ia为电流;T为伺服电机的驱动力矩;Tf为方位轴运动时的摩擦力矩;ω为方位轴运动角速度。Ea和T的计算表达式为:

Ea=keω,T=kmia

(2)

其中:ke为反电动势系数;km为力矩系数。联立(1)式和(2)式,可得方位轴的机电动力学方程为:

(3)

本文分析基于库仑和LuGre 2种摩擦模型下的方位轴伺服控制效果。库仑摩擦力矩是一个常数,即Tf=Tc。LuGre摩擦力矩的计算公式为:

(4)

其中:z为支撑部件接触面鬃毛的平均变形;σ0、σ1为动态摩擦系数;μ为黏性摩擦系数。基于摩擦模型补偿控制的方位轴仿真原理框图如图2所示。其中:最左边的输入信号模块为期望的角速度信号;期望的角位置信号可以通过积分得到;子系统模块为基于摩擦模型补偿模块;模块f(u)根据仿真条件可设置为库仑摩擦模型和LuGre摩擦模型。仿真在Matlab/Simulink中进行。

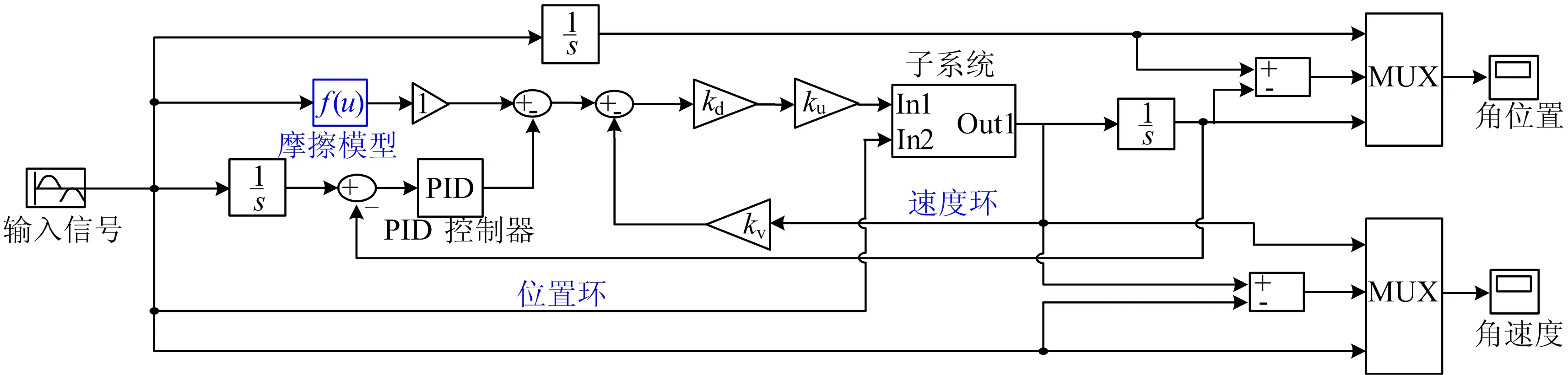
图2 基于摩擦模型补偿控制的方位轴仿真框图

2 方位轴运动性能仿真

仿真研究过程中,期望的角位置信号为正弦形式S=Asin(2πft),A为幅值,f为运动频率;期望的角速度信号为S′=2πfAcos(2πft);卫星跟踪转台保精度工作速度为0.02～6.00°/s,最大工作速度为8.00°/s[13]。本文研究中幅值A固定为5.00°,即保持0.087 3 rad不变。

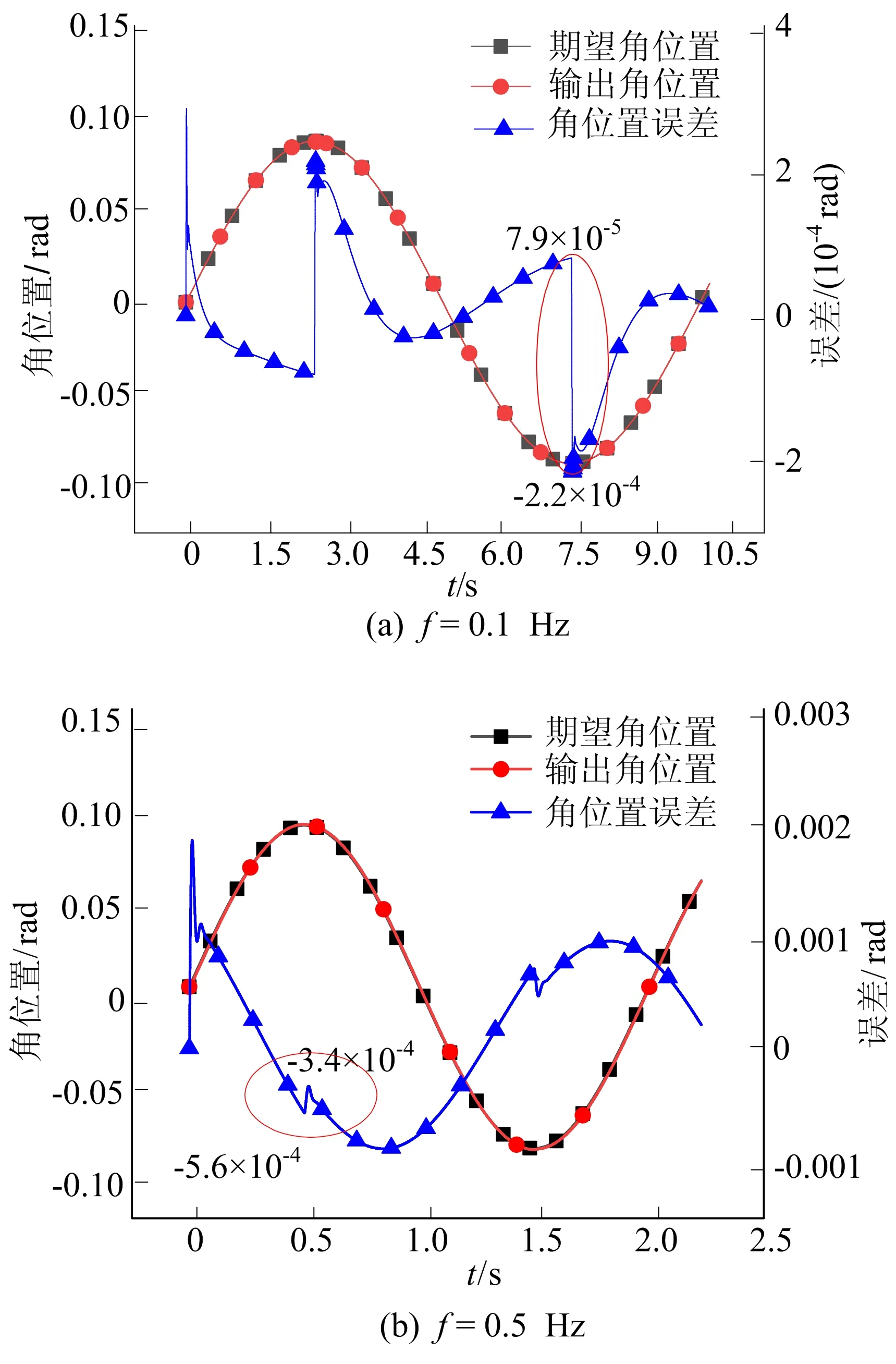
运动频率分别为0.1、0.5、1.0 Hz时,库仑摩擦力矩对方位轴角位置跟随性能的影响如图3所示。图3中信息包含期望角位置信号、实际输出角位置信号及两者之间的误差。在方位轴刚启动时,伺服电机存在一定的响应时间,影响伺服控制效果,角位置跟随误差会陡增。在连续运转中,对转台运动性能影响最大的时刻是轴系到达最大角位置处,此时伺服电机需要反向运转,存在减速再加速的动作,此时如果伺服控制效果不好,那么极易出现抖颤现象,影响后续的跟随效果。

从图3可以看出:当频率f=0.1 Hz时,在方位轴最大角位置处误差跳跃程度比较大,最大误差与最小误差的偏差为3×10-4rad;当f=0.5 Hz时,位置误差的波形基本呈现出正余弦变化规律,表明跟随效果较好,最大误差与最小误差的偏差为2.2×10-4rad;当f=1.0 Hz时,位置误差波形与正余弦波形更加接近,且最大误差与最小误差的偏差为7×10-5rad。这表明在最大角位置处,误差跳跃程度随频率f的增大而减小,伺服控制效果也随之变好。在幅值一定的情况下,低频意味着低速,伺服控制系统会产生低速不平稳现象,速度会出现脉动,角位置跟随性能差甚至会出现卡死现象[14]。

运动频率分别为0.1、0.5、1.0 Hz时,库仑摩擦力矩对方位轴角速度跟随性能的影响如图4所示。

角速度信号形式为S′(t)=2πfAcos(2πft),幅值A固定为0.087 3 rad不变。随着频率f的增大,速度峰值会随之增大。在方位轴启动时刻,输出的实际角速度波动很大,这与上文提到的伺服电机响应特性有关。

由图4可知,在角位置最大处即角速度速度反向处,速度误差会发生急剧的波动,这会影响到卫星跟踪转台的连续稳定运转。当f=0.1 Hz时,速度波动的最大值为3.8×10-3rad/s;随着频率f的增大,输出速度的波动程度越来越小,当f=0.5 Hz时,速度波动的最大值为3.3×10-3rad/s;当f=1 Hz时,速度波动的最大值为1.3×10-3rad/s,此时速度误差的波动非常小。这表明低频下方位轴的速度跟随特性较差,与位置特性的分析相吻合。低频下基于库仑摩擦模型的摩擦补偿效果较差,最大位置处的波动会导致伺服控制系统不易收敛,此时电机可能因处于抖颤状态而不能正常工作。需要说明的是,在分析过程中采用绝对误差来跟踪比较性能。这是由于输入的正弦信号必然存在角位置为0的情况,此处对应的绝对误差无论多小都会使得相对误差趋于无穷大,不适合采用相对误差结果进行比较;在同样的幅值下,采用绝对误差进行比较更为合理;且摩擦补偿控制实质为前馈控制,此误差并不作为反馈信号施加到控制系统中。

运动频率为0.1、0.5、1.0 Hz时,LuGre摩擦力矩对方位轴角位置跟随性能的影响如图5所示。

图5 不同运动频率下LuGre摩擦力矩对角位置跟随性能的影响

由图5可知,与库仑模型下的控制效果明显不同的是,在方位轴启动时刻,角位置误差没有发生明显的波动,角位置跟随比较平稳。这是由于LuGre摩擦模型考虑了接触表面在外载荷下的变形,其包含了摩擦力未达到最大静摩擦力矩之前界面的微小位移,能较为准确地描述非线性摩擦行为。在最大角位置处出现了平顶现象，频率f=0.1 Hz时平顶现象持续时间大约1.5 s;随着频率f的增大,平顶现象逐渐减弱,f=0.5 Hz时,平顶持续时间变为0.5 s左右;f=1.0 Hz时,平顶现象持续时间大约为0.2 s。这种平顶现象在现实中的伺服控制中经常可见[15],表明基于LuGre模型下的控制仿真更加接近实际。

运动频率为0.1、0.5、1.0 Hz时,LuGre摩擦力矩对方位轴角速度跟随性能的影响如图6所示。

图6 不同运动频率下LuGre摩擦力矩对角速度跟随性能的影响

由图6可知:当频率f=0.1 Hz且方位轴刚启动时,库仑模型下角速度误差由0突变成0.1 rad/s,而在LuGre摩擦模型下的角速度误差突变不足0.01 rad/s;当频率f增大后,角速度误差突变的幅度逐渐增大,这与库仑模型是一致的。角速度误差在最大角位置处并未出现波动现象:当f=0.1 Hz时,最大角位置处角速度误差变化0.04 rad/s;f=0.5 Hz时,角速度误差变化0.02 rad/s;f=1.0 Hz时,角速度误差变化0.005 rad/s。

从上述仿真结果可以发现:基于库仑摩擦模型的摩擦补偿控制虽然在其他区域有较好的运动跟随特性,但在启动时刻和最大角位置处误差波动大,导致卫星跟踪转台稳定运转的可靠性降低,原因在于库仑摩擦模型是一种静态的简化模型,与真实的非线性摩擦行为差异较大;而LuGre模型因考虑了最大静摩擦力矩之前的微小变形,更接近真实的摩擦行为,使得在启动时刻和最大角位置处误差波动较好,转台运转将更加平稳。

接下来,将基于优选的LuGre摩擦模型分析摩擦力矩数值变化对方位轴运动跟随性能的影响,主要通过改变(4)式中黏性摩擦系数μ来实现。如上文所述,卫星跟踪转台是在地面环境下安装调试的。地面模拟试验普遍采用的是运动环境模拟,即在地面上营造出太空微重力环境[16]。实际上,转台在地面调试和太空运行中的最主要差别在于轴系摩擦力矩的变化。理论上可以分析得到2种工况下的摩擦力矩特性,并可以在地面调试中将转台轴系的摩擦力矩人为调节成太空运行工况下的数值,此时得到的运动学性能即为太空运行的真实性能。因此，研究不同摩擦力矩下的转台性能可为这种地面模拟思路提供数据参考。

不同LuGre摩擦力矩下方位轴运动跟随性能的变化如图7所示。由图7可知,随着黏性摩擦系数μ的增加,角位置和角速度跟随性能都降低,其误差都逐渐增大。角位置跟随曲线的平顶现象也随着黏性摩擦系数的增大而变严重。由于摩擦补偿控制是一种前馈控制方法,当黏性摩擦系数增大时,轴系的摩擦力矩会随之增加,伺服电机的输出力矩要随之进行调节。电机本身的调节特性一定且摩擦力矩在低频运动下是强非线性的,输出力矩数值越大则与真实的摩擦力矩间的误差就越大,这会导致轴系的跟随性能退化。不同摩擦力矩下的仿真研究不仅为地面模拟试验方案提供了数据参考,也为转台精度增长提供了另一可行途径,即通过降低支撑轴承的滚动摩擦系数来提高运动精度,如采用陶瓷轴承或其他低摩擦轴承。

图7 LuGre摩擦力矩数值变化下的方位轴跟随性能

3 结 论

本文以二轴卫星跟踪转台中的方位轴为对象,研究摩擦力矩对其运动性能的影响,主要结论如下:

(1) 无论是库仑摩擦模型还是LuGre摩擦模型,方位轴在低频下的运动跟随性能较差,应重点关注。

(2) 在最大角位置处,基于库仑模型的摩擦补偿控制容易出现波动;而LuGre摩擦模型考虑了最大静摩擦力矩之前的接触界面变形,与实际的摩擦行为更接近,因此摩擦补偿控制效果好,在最大角位置处速度误差波动不明显。

(3) 通过改变LuGre模型中的黏性摩擦系数大小研究了不同摩擦力矩下方位轴的运动跟随性能,证明小摩擦力矩有助于卫星跟踪转台的伺服控制效果。