一种面向车内噪声控制的改进变步长LMS算法
钱梦男, 卢剑伟, 晏桂喜, 郭嘉豪
(1.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 2.合肥工业大学 机械工程学院,安徽 合肥 230009)
20世纪60年代Widrow和Hoff提出最小均方(least mean square,LMS)算法,便以其结构简单、计算量小、对硬件要求低等优点而被广泛应用于包括有源噪声控制(active noise control, ANC)在内的自适应信号处理领域。对于LMS算法,由于其步长固定,不能兼顾收敛速度和稳态误差,在算法的收敛范围内,算法步长设置越大,其收敛速度越快,同时使得稳态误差变大;反之亦然。针对此问题,国内外学者提出了很多改进的算法[1-11]改善LMS算法性能。这些算法可以分为2类:一类是变换域LMS;另一类是时域LMS。由于时域算法的结构简单和鲁棒性,在ANC系统中获得广泛的应用,而时域中的改进算法主要分为如下2种:
(1) 变抽头长度的LMS算法。文献[1-3]所提出的算法,通过调整抽头长度使LMS算法性能有所提升,但是这些算法在变换抽头长度的同时要求抽头长度为整数,造成计算较为复杂,实际应用难度较大。
(2) 变步长的LMS算法。通过构造误差和步长之间的关系,实现对步长的控制。此种算法的控制原则为:初始阶段误差值较大,采用大步长加快收敛速度;收敛后误差值接近0时,采用小步长来降低稳态误差。文献[4]基于Sigmoid函数提出SVSLMS算法,但是该算法在稳态误差接近0时,步长变化仍然较大。为此,文献[5-6]对文献[4]中的算法进行了改进。文献[7]采用Tanh函数对LMS算法进行了改进;文献[8]提出了基于Sinh函数进行改进的变步长算法;文献[9-10]提出了基于对数的变步长算法;文献[11]提出了一种分段式的变步长算法。
上述改进算法在兼顾收敛速度与稳态误差方面有所改进,但仍在计算量和收敛速度方面有待进一步改善,特别是用于车载ANC系统时,还不能很好地满足硬件的嵌入式使用的需求。为此,本文在LMS算法的基础上,提出了一种基于Softsign的变步长算法,改善定步长LMS算法收敛速度和稳态误差的矛盾,兼顾算法的计算量,并通过算例分析,来验证算法的性能。
1 LMS算法
LMS算法是基于最速下降法的迭代适应算法,通过调整滤波器参数,适应输入信号x(n)随时间变化的特性,使系统响应信号y(n)与期望响应d(n)之间的误差e(n)达到最小,原理如图1所示。
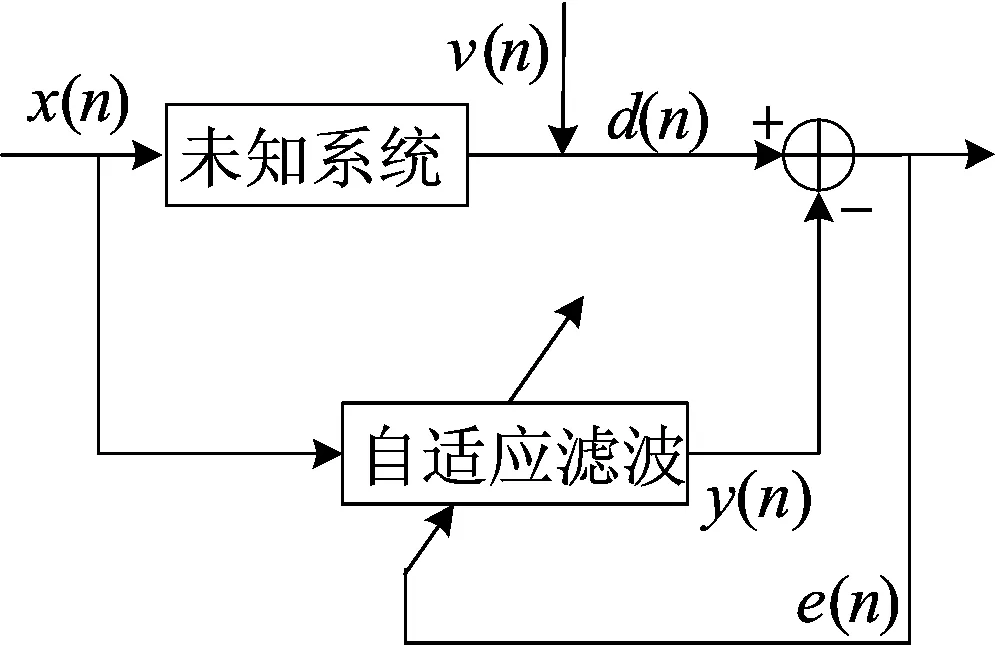
图1 自适应滤波原理
其迭代过程如下:
y(n)=W(n)TX(n)
(1)
e(n)=d(n)-y(n)
(2)
W(n+1)=W(n)+2μe(n)X(n)
(3)
其中:X(n)为n时刻的输入信号矢量;W(n)为n时刻自适应滤波器的权系数;μ为算法的步长。LMS算法的收敛条件为0<μ<1/λmax,其中,λmax为输入信号自相关矩阵的最大特征值。
2 一种改进的变步长算法
2.1 改进的变步长算法
Softsign函数与Tanh函数、Sigmoid函数具有相似的函数形状、过零点、单调平滑的函数曲线,通过简单调整可以很好地满足步长调整原则,且与Sigmoid函数、Tanh函数相比较不含指数项,计算更加简单。因此,本文根据变步长算法改进原则,利用Softsign函数特性,提出一种改进的变步长算法。
(4)式是利用Softsign函数的调整过的步长函数,其函数图像如图2所示。从图2可以看出,在误差e(n)趋近于0时,步长μ(n)变化依旧很快,会造成算法稳态误差较大,且步长μ(n)与误差e(n)的函数图像不可调整。
(4)
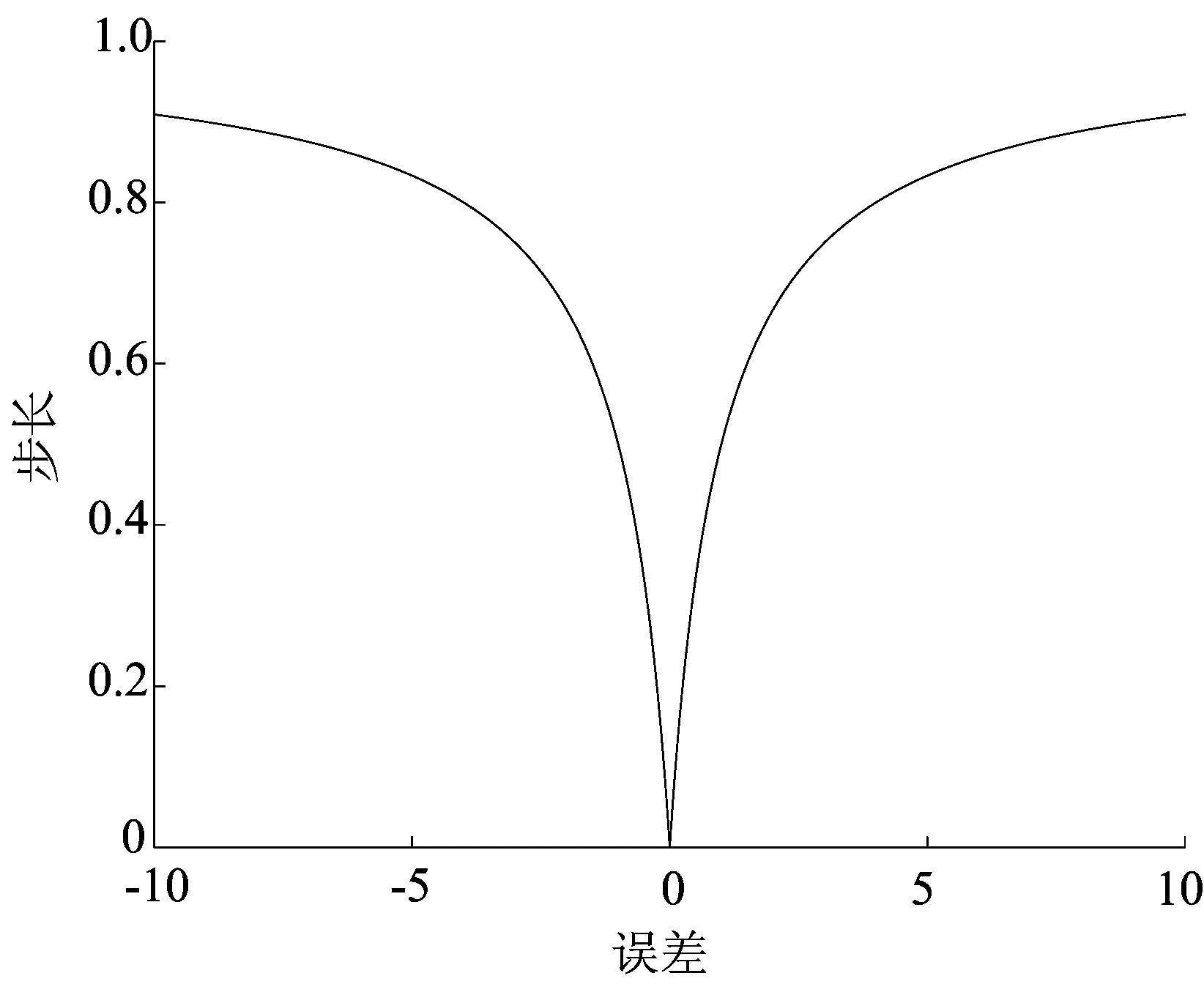
图2 步长与误差之间的关系
针对上述问题,本文对(4)式进行了改进,引入了控制参数α、β、m,调整后的变步长函数为:
(5)
由此得出一种改进的基于Softsign函数的变步长LMS算法。改进的变步长算法的收敛条件为0<β/α<1/λmax。
2.2 参数对算法的影响
下面利用误差e(n)与μ(n)之间的函数曲线分析各参数具体的影响,即分析α、β、m对算法性能的具体影响,如图3所示。
由图3可知:① 当β、m值固定时,在收敛范围内,α值越大,算法的初始收敛步长越小,收敛越慢;② 当α、m值固定时,在收敛范围内,β值越大,算法的初始收敛步长越大,收敛越快;③ 当α、β的值固定时,m值越大,算法在误差e(n) 趋近于0时,步长μ(n)的变换趋势越平缓,且此时算法在误差e(n)较大时拥有更大的步长μ(n),但是m值越大,算法的计算复杂程度也会随之增加。
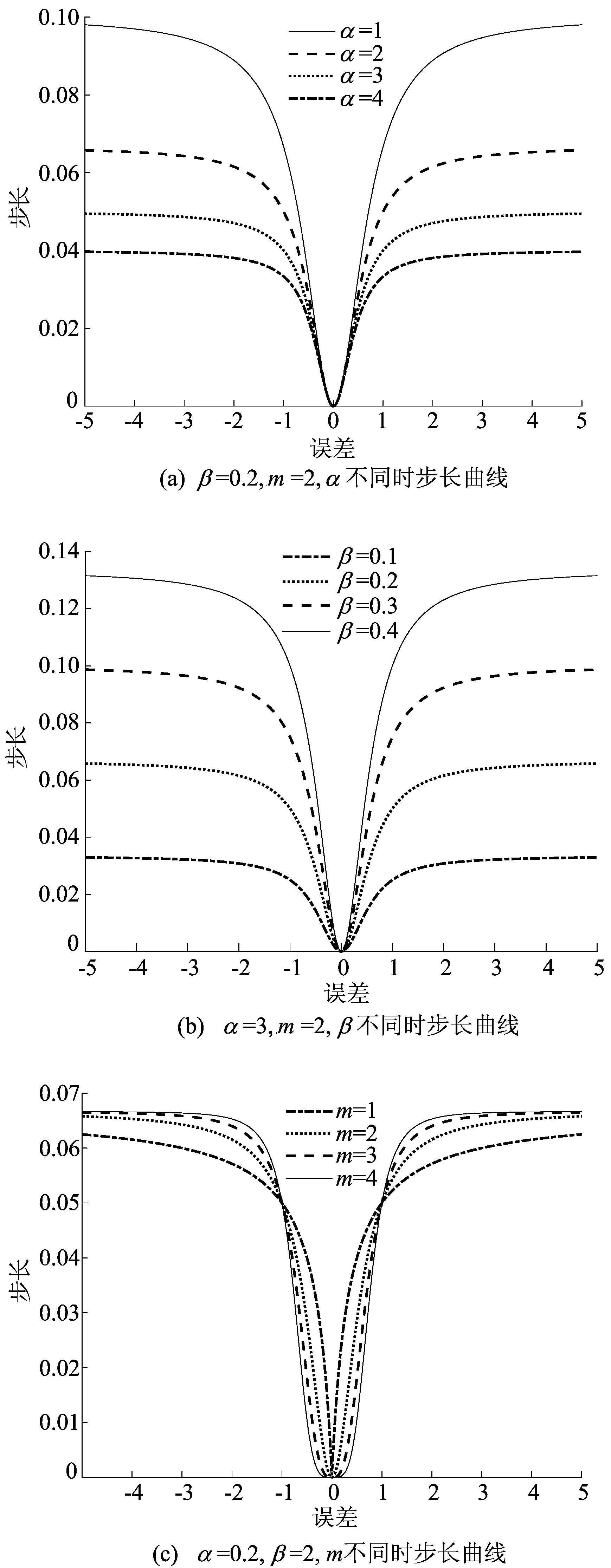
图3 参数对步长曲线的影响
3 新的变步长算法仿真验证
3.1 改进的变步长算法性能验证
为了验证提出的改进的变步长算法性能,利用Matlab软件,通过仿真算例对该算法进行分析。设置仿真参数为:噪声输入x(n)是均值为0、方差为1的高斯白噪声;干扰信号v(n)是均值为0.04、方差为1的高斯白噪声,且与x(n)不相关;自适应滤波器的长度为4;采样点数为500;试验次数为200。对均方误差进行统计分析,得到算法的收敛曲线,如图4所示。
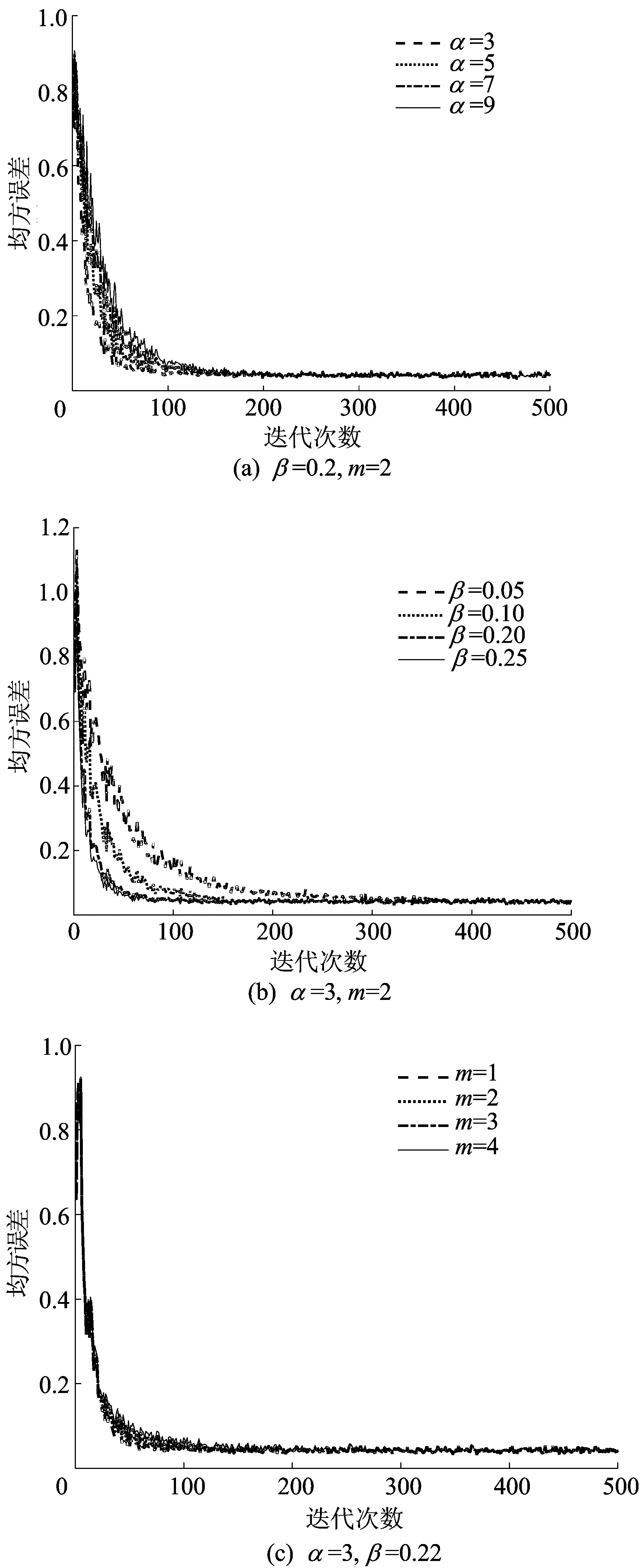
图4 参数对收敛曲线的影响
由图4可知:① 固定β、m值,随着α的增大,收敛速度变缓;② 固定α、m值,随着β值的增大,收敛速度变快;③ 固定α、β值,m值增大可以降低算法稳态误差,但是从图4c可以看出,此方式对于稳态误差并不具备明显改善效果,而且随着m增大,算法的初始收敛速度有一定的降低,且会增加算法计算复杂度。图4结果与图3结果相印证,说明了本文算法改进的有效性。
3.2 与其他算法性能比较
为了验证本文算法在性能上的优势,将本文算法与定步长的LMS算法及文献[7]中的Tanh-LMS算法相比较。文献[7]中步长μ(n)与误差e(n)函数关系为:
(6)
设置仿真参数为:噪声输入与3.1节一致;滤波器长度为4;定步长算法的步长μ=0.01;(6)式仿真参数与文献[7]中相同,α=100,β=0.04,m=1。本文算法设置参数为:α=3,β=0.25,m=1,采样点数为500;计算200次取均方误差。仿真结果如图5所示。
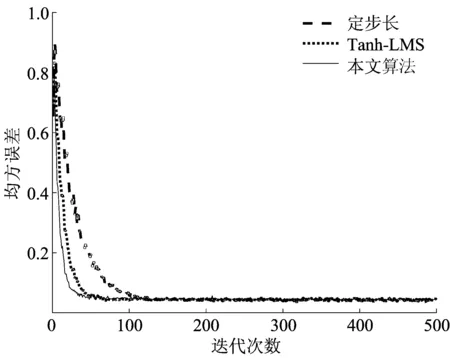
图5 3种算法收敛速度比较
从图5可以看出,本文算法在与定步长LMS算法及Tanh-LMS算法拥有相似的稳态误差情况下,在收敛速度上定步长180次后达到收敛效果,文献[7]在80次后达到收敛效果,而本文算法在50次后就能实现很好的收敛,可以看出本文算法具有更快的收敛速度。
3.3 算法计算量比较
算法计算量上比较,因定步长算法不含步长的变化项,其稳态误差与收敛速度兼顾性最差,其计算量本文不予比较。现将本文算法与文献[7]中Tanh-LMS算法相比较,结果见表1所列,算法参数值为3.2节仿真参数。从表1可以看出,本文算法在计算量上明显小于Tanh-LMS算法,尤其是本文算法不含指数项,对车载ANC系统硬件实现的要求更低。

表1 本文算法与文献[7]算法计算量比较 单位:项
3.4 在车内噪声控制中的应用仿真
为了验证本文提出的算法在车载ANC系统中的应用优势,利用采集到的车内噪声数据对算法进行降噪性能仿真比较。采样设备为东华DH5922N动态信号测试仪,频率为2 000 Hz。双通道采集车内数据,将通道1与通道2采集到的数据分别作为输入信号和期望信号。
选取200个连续噪声点建立自适应滤波器。然后随机选取未参与训练的1 000个连续点作为噪声信号进行降噪。分别将LMS算法、Tanh-LMS和本文提出的算法应用于车内自适应降噪处理,设置参数与3.2节的仿真参数相同,结果如图6所示。
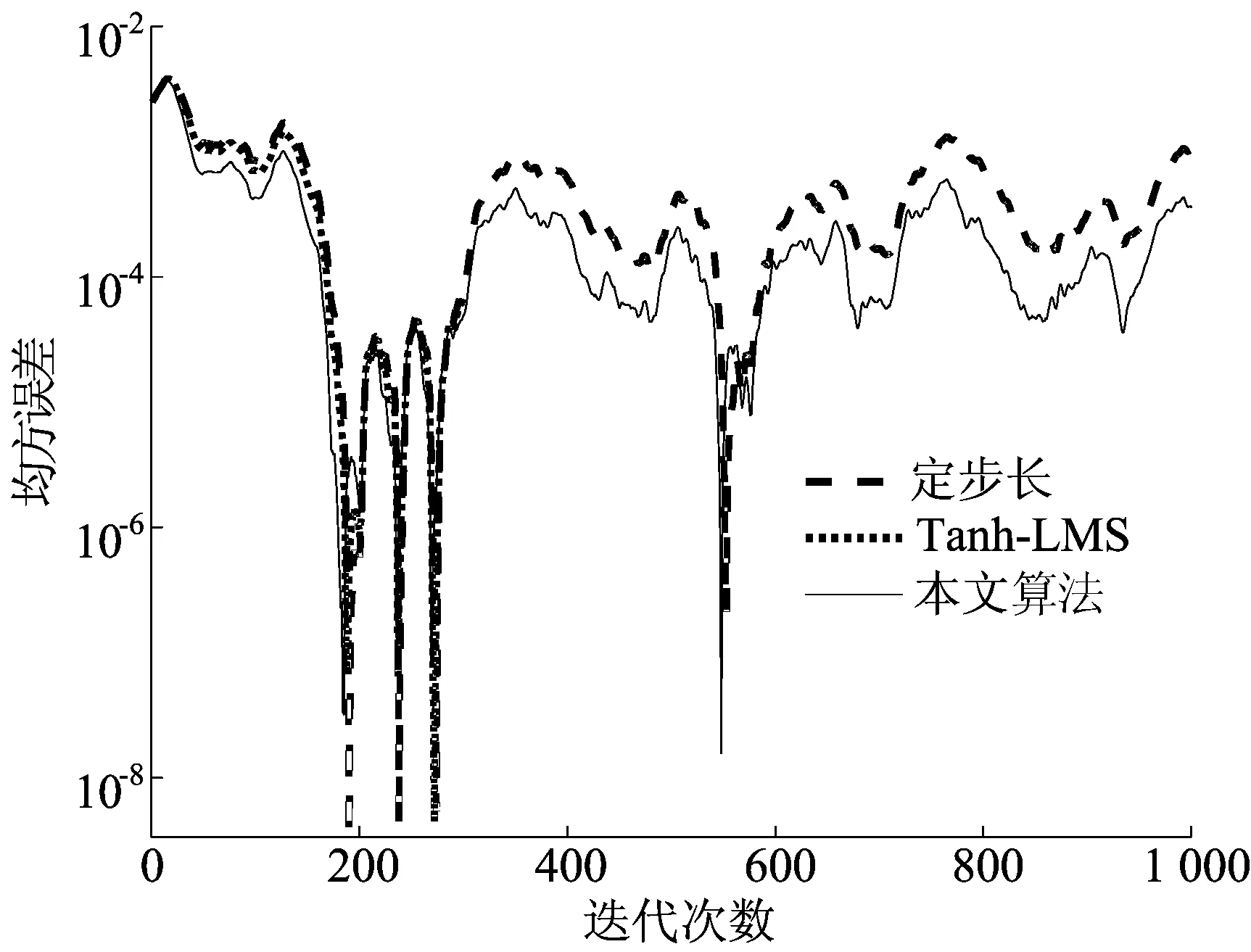
图6 车内噪声误差信号曲线
从图6可以看出,在利用车内噪声数据进行自适应降噪仿真时,本文算法在收敛速度和稳态误差值上优于LMS算法和Tanh-LMS算法,说明本文算法的噪声抵消效果更好。
4 结 论
本文针对ANC系统中定步长LMS算法不能兼顾收敛速度和稳态误差的缺点,基于Softsign函数,建立了步长μ(n)与误差e(n)之间的函数关系,提出了一种改进的变步长算法,并将其应用于车内噪声控制中。仿真结果表明,本文算法在兼顾收敛速度和稳态误差方面优于LMS算法和Tanh-LMS算法;在计算量方面与Tanh-LMS算法相比具有明显的优势;改进的算法在车内噪声控制中的效果优于其他2种算法,提高了其在硬件上的应用性。
——中国制药企业十佳品牌

