基于MFO-SVR的球磨机出粉量估算
宋 宇, 陆金桂
(南京工业大学 机械与动力工程学院,江苏 南京 211816)
0 引 言
在整个火力发电过程中,球磨机是必不可少的辅助设备,它将煤块磨制成煤粉,使其充分燃烧。因为球磨机运行特性复杂,各参数之间耦合现象严重,导致球磨机出粉量难以直接测量,也难以使用简单的数学模型进行精确的间接测量,所以在最优工况不明确的情况下,工作人员常常使球磨机在低负荷区运行,大大降低了出粉量,同时还增加了能耗。因此,寻找合适的方法解决球磨机出粉量的测量问题变得极为重要。
在实际生产中,需要采取一些间接的方法进行测量。在间接测量中,目前采用的差压法、功率法、噪声法、轴承振动法、油压法、气压差动法、应变法等方法都是依靠单一变量来表征存煤量进而得到球磨机的出粉量,但是通过这些方法得到的球磨机出粉量的误差比较大。近年来,随着测量技术的发展与完善,基于多变量的软测量方法被逐渐应用于测量领域[1-3]。其基本思想是以数据驱动为基础,构建易测量的变量与那些难测量的变量之间的数学关系模型,通过测量那些可测量的变量来间接测量那些难测量的变量。常见的软测量建模方法有基于黑箱理论的神经网络法[4-5]以及支持向量回归机(support vector regression,SVR)法[6-7]。
人工神经网络具有很强的鲁棒性和容错性,可以拟合所有复杂的非线性关系,且有一定的学习能力和自适应性,因此可以用来预测球磨机的出粉量。文献[8]以最优拉丁超立方法选取的数据作为训练样本,建立了球磨机出粉量的BP神经网络估算模型,降低了估算误差,提高了泛化性; 文献[9]借助机理分析和混沌信息处理计算,建立了球磨机出粉量的软测量模型,对球磨机出粉量进行了较为精确的估算; 文献[10]提出了一种基于Takagi-Sugeno型模糊规则的火电厂球磨机出粉量预测方法,提高了电厂效率。但是球磨出粉量的神经网络模型由于存在以下缺点,导致使用结果并不理想。
(1) 神经网络模型的参数都是人为设定的,通过试凑法经过微调得到一组最优参数,这需要做大量的试验,增加了时间成本。
(2) 神经网络模型的训练以传统统计学为基础,基于经验风险最小化原则。这需要无穷多的样本数据支撑,实际上训练样本是有限的,因此导致了网络的泛化性差,预测精度不高。
(3) 神经网络采用逆梯度法调整权、阈值,经常陷入局部最优解。当网络层数过多时还会出现“梯度消失”现象。
相比于神经网络而言,SVR的训练以统计学理论为基础,基于结构风险最小化原则。SVR的复杂程度仅取决于支持向量的个数,主要针对小样本情况,并且从本质上避免了从归纳到演绎的过程,可以比较准确地预测出球磨机出粉量。文献[11]结合球磨机的机理对影响球磨机出粉量的主要因素进行分析,选择合适的辅助变量,建立了球磨机出粉量的SVR模型,得到了较为精确的预测结果;文献[12]结合混沌灰熵分析理论,建立了球磨机出粉量的GECA-ε-SVR模型,对球磨机出粉量进行了精确的估算。
虽然球磨机的SVR模型有诸多优点,但是惩罚因子C以及核函数系数g影响着SVR的预测精度,并且它们很难确定。目前确定C和g的方法有k折交叉算法[12]、网格搜索法[13]、模拟退火(simulated annealing,SA)[14]、粒子群优化(particle swarm optimization,PSO)算法[15]、遗传算法(genetic algorithm,GA)[16]。前两者是非智能优化算法,搜寻的结果都不太准确,很难确定较优的参数。后三者属于智能优化算法,SA是个体优化算法,虽然在统计上能100%找到全局最优解,但是计算复杂;PSO和GA是群体优化算法,理论上群体优化算法要好于个体优化算法。PSO计算简单,操作方便,但随着迭代次数的增加种群多样性降低,且易陷入局部最优解;GA虽然保证了种群多样性,但计算量大,计算结果不稳定,易陷入局部解。相比而言,飞蛾火焰优化(moth-flame optimization,MFO)算法[17-19]计算简单,能较好地平衡局部搜索能力和全局搜索能力。因此本文尝试着使用MFO算法来确定球磨机出粉量SVR模型的参数,对球磨机出粉量进行精确估算。
本文首先介绍了MFO算法的原理,并将MFO算法和SVR相结合建立了球磨机出粉量的MFO-SVR模型。将球磨机出粉量的MFO-SVR模型和PSO-SVR模型、GA-SVR模型进行对比,验证了MFO-SVR模型具有较优越的预测能力以及较好的泛化性。
1 MFO算法
1.1 算法原型
飞蛾扑火优化算法的灵感来源于“飞蛾扑火”这一生物行为。“飞蛾扑火”并不是飞蛾的自杀行为,而是由飞蛾本身具有的横向定位机制引起的,如图1所示。在这种方法中,由于飞蛾离月球很远,飞蛾通过保持与月球的固定角度来飞行,可以保证飞蛾在一条直线上长距离飞行。

图1 横向定位机制
当飞蛾看到人造光源时,它们试图与光线保持一个相似的角度直线飞行。但是,这样的光线比月球的光线距离近很多,因此保持与光源相似的角度会导致飞蛾无用或致命的螺旋飞行路径,飞蛾最终会向光源收敛,如图2所示。

图2 “飞蛾扑火”生物行为
1.2 算法原理
在MFO算法中,假设候选解是飞蛾,问题的变量是飞蛾在空间中的位置。因此,通过改变其位置向量,飞蛾可以在一维、二维、三维或超维空间中飞行。
因为MFO算法是基于种群的算法,所以用矩阵M表示飞蛾的集合,即
(1)
其中:n为飞蛾种群数目;d为待求变量的维度;mi,j可以通过使用随机分布来给出,即
mi,j=[bu(i)-bl(i)]rand()+bl(i)
(2)
其中:mi,j为矩阵M第i行第j列的值;bu(i)、bl(i)分别为第i个飞蛾位置的上限和下限;rand()为在区间[0,1]中生成的均匀分布随机数。
对于所有飞蛾种群,还假设有一个数组OM用于存储相应的适应度值,即
OM=[OM1OM2…OMn]T
(3)
火焰是算法中的另一个关键因素,类似于飞蛾矩阵M,火焰矩阵用F表示,火焰的适应度值用数组OF表示,即
(4)
OF=[OF1OF2…OFn]T
(5)
在MFO算法中,飞蛾矩阵M表示在算法搜索过程中执行移动变化的实际主体,而火焰F代表着经过飞蛾M搜索之后到目前为止所得到的最优解。因此,如果得到了一个更好的解,就会保证每只飞蛾在该最优值的附近进行搜索,以免错过任何最优解。
MFO算法计算过程可以描述如下:
MFO=(I,P,T)
(6)
I用于产生一个初始随机飞蛾群,并且计算相应的适应度函数值。该模型可以表示为:
I:φ→{M,OM}
(7)
P代表飞蛾在空间范围内的搜索原理;飞蛾矩阵M输入P中,输出更新之后的矩阵M′,即
P:M→M′
(8)
若算法达到了设置的停止条件,则T的值为真;若不满足,则T的值为假。表示为:
T:M→{true,false}
(9)
综上所述,当I函数初始化之后,P函数进行迭代更新,运行直至T函数返回为真,则算法运行结束,一般流程框架如下:
M=I()
WhileT(M) is equal to false
M=P(M);
end
在初始化飞蛾的种群数、位置以及确定了适应度函数之后,飞蛾种群的更新机制为如下螺旋线:
Mi=S(Mi,Fi)=Dieb tcos(2πt)+Fj
(10)
其中:Mi为第i个飞蛾;Fj为第j个火焰;S为螺旋函数;Di=|Mi-Fj|为第i个飞蛾距第j个火焰的距离;b为定义对数螺旋形状的常数;t为[-1,1]中的随机数。控制飞蛾与火焰的距离,对数螺旋线如图3所示。
图3中,t越小,飞蛾离火焰越近,通过改变t,飞蛾可以到达火焰周围的位置,增强了算法的局部寻优能力。
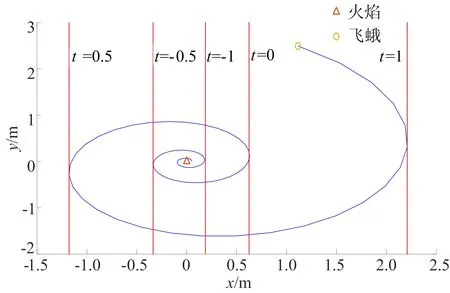
图3 对数螺旋线
为了避免所获得的解为局部最优值的情况,在每次迭代更新列表后,火焰根据它们的适应度数值大小排序,然后飞蛾更新它们相对于火焰的位置。
采用计算公式使火焰数量在迭代过程中不断减少,即
(11)
其中:l为当前迭代次数;N为最大火焰数目,lmax为最大迭代次数;round表示取整。
P函数的执行步骤如下:
用(11)式计算更新火焰的数量
计算飞蛾的适应度函数值
if迭代次数为1
F=sort(M);
OF=sort(OM);
else
F=sort(Mt-1,Mt);
OF=sort(OMt-1,OMt);
end
fori=1:n
forj=1:d
计算飞蛾与相应火焰之间的距离Di=|Mi-Fj|;
采用(10)式更新飞蛾与相应火焰之间的距离M(i,j);
end
end
综上所述,执行P函数直到T函数返回ture。P函数终止后,最佳飞蛾作为获得的最佳近似值返回。
2 MFO-SVR算法
用SVR预测球磨机出粉量等价于求解合适的惩罚因子C以及RBF核函数系数gamma,为了提高球磨机出粉量的预测精度,使用MFO算法来确定参数C和gamma,算法流程如下。
(1) 设置参数。飞蛾和火焰的数目n=60,最大迭代次数lmax=100,变量的维度d=2,飞蛾位置的上限bu=[30,100],下限bl=[-30,-100]。
(2) 飞蛾位置初始化。在搜索空间内随机生成飞蛾位置,M(i,:)=[mi,1mi,2]=[gC],迭代次数l=1。其中,M(i,:)为飞蛾矩阵M的第i行的行向量。
(3) 计算适应度值。将mi,1和mi,2输入SVR模型中以进行球磨机出粉量的预测。根据预测结果,可以计算出适应度函数的相应值。本文采用平均绝对百分比误差(mean absolute percentage error,MAPE)为适应度函数,计算公式为:
(12)
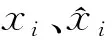
(4) 将飞蛾位置按适应度值从小到大排序,赋给火焰。
(5) 飞蛾围绕火焰按(10)式,更新其位置。其中:b=1;t为[-1,1]中的随机数。
(6) 记录当前最优火焰适应度值。
(7) 根据(11)式减少火焰数量,l=l+1。
(8) 判断是否达到最大迭代次数,若达到则输出最优火焰位置和其适应度值,否则转到步骤(4)。
球磨机出粉量的MFO-SVR算法流程如图4所示。

图4 球磨机出粉量的MFO-SVR算法流程
3 计算实例
3.1 数据获取
本文的研究对象为重庆某电厂1#球磨机,由于球磨机结构复杂,其磨煤过程被许多因素所干扰,同时这些因素之间的关系又具有高度的非线性特点,通过数据服务器SCADA,从电厂DCS数据库中采集时发现球磨机现场测点较多,采集的数据也较为复杂,在现场工作人员的帮助下,采集了该球磨机1 d的运行数据,剔除了一些异常样本,最终采用系统抽样从中筛选了500组样本数据,见表1所列。
对上述数据进行归一化处理,即
(13)

随机选取450组作为训练样本,其余50组作为测试样本,分别建立球磨机出粉量的MFO-SVR、PSO-SVR、GA-SVR模型。

表1 球磨机样本数据
3.2 参数设置
(1) MFO-SVR算法。飞蛾和火焰的数目n=60,最大迭代次数lmax=100,变量的维度d=2,对数螺旋线参数b=1,SVR的不敏感系数ε=0.001,g∈[0,30],C∈[0,100]。
(2) PSO-SVR算法。种群的规模n=60,最大迭代次数为lmax=100,变量的维度d=2,学习因子c1=c2=1.78,惯性权重ω=0.7,SVR的不敏感系数ε=0.001,g∈[0,30],C∈[0,100]。
(3) GA-SVR算法。种群的规模n=60,最大迭代次数为lmax=200,交叉概率Pc=0.6,变异概率Pr=0.01,SVR的不敏感系数ε=0.001,g∈[0,30],C∈[0,100]。
3.3 实验结果与分析
根据球磨机的3个主要的平衡方程[20],选择对球磨机出粉量贡献度大的进出口差压、出口风粉压力、出口风粉温度、进口一次风量、进口一次风压、进口一次风温、电流等因素作为输入,以球磨机出粉量为输出,建立了球磨机出粉量的MFO-SVR、PSO-SVR、GA-SVR模型,其预测结果如图5、图6所示。


图6 MFO-SVR算法迭代曲线
从图5可以看出:GA-SVR模型的两端有发散的迹象,预测值和实际值的走向趋势相反,说明GA-SVR模型的泛化性能不好,而MFO-SVR、PSO-SVR模型两端的预测值和实际值走向趋势相同,表明具有较好的泛化性能。
从图6可以看出:在前5次迭代时MAPE下降得比较快,这是由于MFO算法充分发挥了前期较强的全局搜索能力;第6次~第18次迭代期间,虽然MAPE下降的速度变慢,但是也匀速下降,这是由于MFO后期发挥了较强的局部搜索能力,在第18次迭代时锁定了全局最优解。由此可以看出MFO算法能较好地平衡局部搜索能力和全局搜索能力。
为了验证模型的泛化能力和寻优精度,本文将平均绝对误差(mean absolute error,MAE)、MAPE、均方根误差(root mean square error,RMSE)和决定系数(R-square,R2)4个统计学检验数据作为模型的评价指标。
MAE的计算公式为:
(14)
MAPE的计算公式为:
(15)
RMSE的计算公式为:
(16)
R2的计算公式为:
(17)
其中:xi、yi分别为实际值和估算值;n为数据样本的个数。
球磨机出粉量软测量模型误差见表2所列。

表2 球磨机出粉量软测量模型误差
从表2可以看出:前3项误差评判指标,球磨机出粉量的MFO-SVR模型最低,PSO-SVR模型其次,GA-SVR模型最高;MFO-SVR模型的平方相关系数R2比其他算法的更接近于1,其次是PSO-SVR模型的,GA-SVR模型的离1最远。这表明球磨机出粉量的MFO-SVR模型具有较好的预测精度和较优的泛化能力,PSO-SVR模型次之,GA-SVR模型最差,与前面预测结果分析相吻合。
4 结 论
(1) 本文借助软测量技术,以进出口差压、出口风粉压力、出口风粉温度、进口一次风量、进口一次风压、进口一次风温、电流等因素作为输入,以球磨机出粉量为输出,建立了球磨机出粉量的MFO-SVR模型,解决了球磨机出粉量的测量问题。
(2) 将所建立的球磨机出粉量的MFO-SVR模型,与其PSO-SVR模型、GA-SVR模型的预测结果进行对比,结果显示MFO-SVR模型的MAE、MAPE、RMSE比其他2个模型低,分别为2.172 4%、3.300 2%、2.848%,其平方相关系数也更接近于1,表明了球磨机出粉量的MFO-SVR模型具有较好的预测精度和较优的泛化能力,更适合球磨机出粉量的软测量。

