轻绳对圆环拉力的冲量大小到底是多少？*——对《绳杆关联系统若干问题研究》一文的再分析

姜付锦 喻 聪

(武汉市黄陂区第一中学 湖北 武汉 430300)

1 问题由来

【题目】[1]如图1所示，将质量为2m重物悬挂在轻绳的一端，轻绳的另一端系一质量为m的环，环套在竖直固定的光滑直杆上，光滑定滑轮与直杆的距离为d.杆上的A点与定滑轮等高，杆上的B点在A点正下方距离为d处，现将环从A处由静止释放，不计一切摩擦阻力，求：

图1 题图

(1)环到达B处时，重物上升的高度h;

(2)若环到达B处时速度大小为v，求此时重物速度大小;

(3)环从A处静止释放到B处过程中，环克服轻绳拉力做的功W;

(4)环从A处静止释放到B处过程中，绳对环拉力的冲量大小 ;

(5)环能下降的最大高度H.

1.1 原文作者对第(4)问的分析

规定向下为正方向，环从A运动B的过程中，因绳对环拉力的冲量不在竖直方向上，运用动量定理非常麻烦.因此对重物、环与重物组成的系统分别应用动量定理，对重物运用动量定理，有

2mgt-I=2m(-v物)-0

(1)

对环与重物组成的系统运用动量定理，有

mgt+2mgt=mv+2m(-v物)

(2)

1.2 笔者的一点疑惑

上题中第(4)问，绳子对环拉力的方向是时刻变化的，绳对重物拉力的方向是不变的.绳对圆环拉力的冲量有两个分方向：水平方向和竖直方向，我们可以先求出拉力在两个方向上的分冲量，再求出它们合冲量即为拉力的冲量.把环与重物组成一个系统，则绳子对环在竖直方向上的冲量与绳子对重物在竖直方向上的冲量不能抵消，故原文中(2)式有误.

对重物用动量定理得

2mgt-IF=2m(-v物)

(3)

对圆环用动量定理得

mgt-Iy=mv

(4)

联立式(3)、(4)整理得

mgt+2mgt-IF-Iy=mv+2m(-v物)

(5)

故笔者以为原文中式(2)结果有待商榷.

2 定量研究

2.1 两个物体速度与夹角的关系

当轻绳与竖直杆的夹角为θ时，设环的速度v1，重物的速度v2，由机械能守恒定律

(6)

环与重物的速度关系

v2=v1cosθ

(7)

联立式(6)、(7)得

v2=v1cosθ=

(8)

2.2 圆环所受拉力的冲量

设绳子的拉力为F，则通过对圆环受力分析可知，圆环的动力学微分方程如下

(9)

将式(9)整理后得

(10)

因为轻绳与竖直杆夹角在减小，所以轻绳绕定滑轮转动的角速度为负值，即

(11)

联立式(10)、(11)两式，得绳子的拉力为

(12)

圆环受到的拉力在水平方向和竖直方向上的冲量分别为

(13)

联立式(8)、(12)、(13)，并积分得

(14)

由式(14)，得圆环受到轻绳拉力的冲量为

(15)

2.3 圆环下落的最大高度

设圆环下降的最大高度为H，则根据机械能守恒定律得

(16)

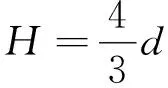
(17)

所以圆环在最低点时绳与杆的夹角为

(18)

3 数值模拟

为了研究问题的方便，不妨设m=1 kg,g=10 m/s2,d=1 m，数值模拟如下.

3.1 圆环与重物的速度与时间关系

图2为圆环与重物的速度与时间关系图像.从图2可以发现，圆环与重物的速度与时间呈周期性变化；它们不是同时达到最大速度，圆环先达到最大速度，重物后达到最大速度；它们速度为零是同时的.

图2 圆环与重物的速度与时间关系

3.2 圆环与重物的速度与角度关系

圆环与重物的速度与角度的关系图像如图3所示.从图3可以发现，圆环达到最大速度时绳与杆的夹角不是60°，此时夹角要比60°大一些；重物达到最大速度时绳与杆的夹角也不是60°，此时夹角要比60°小，与式(18)分析结果吻合.

图3 圆环与重物的速度与角度关系

3.3 圆环与重物的加速度与时间关系

圆环与重物的加速度与时间关系如图4所示.从图4可以发现，圆环开始运动时加速度为g，重物开始时加速度为零；圆环速度最大的时刻比重物速度最大时刻早一些.

图4 圆环与重物的加速度与时间关系

4 结束语

通过以上分析发现，圆环与重物的速度与时间呈周期性变化；它们不是同时达到最大速度，圆环先达到最大速度，重物后达到最大速度，它们速度为零是同时的；圆环达到最大速度时绳与杆的夹角要比60°大；重物达到最大速度时绳与杆的夹角要比60°小；圆环开始运动时加速度为g，重物开始时加速度为零，而且两个物体的加速度与时间变化的周期相等；当圆环在平衡位置微扰时，圆环与重物振动规律的相位差为零，且它们最大速度之比为它们质量的反比；绳子对圆环拉力的冲量没有解析解，只有数值模拟解.