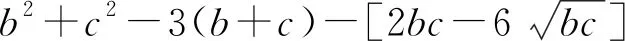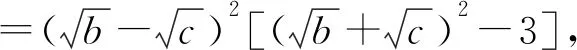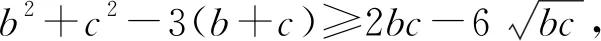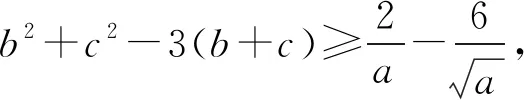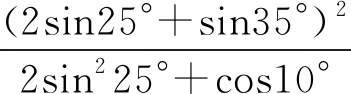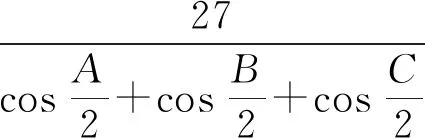数学问题解答

2616平面上给定n个点，任意三点不共线，过任意两点作直线．已知任意两条直线既不平行也不垂直，过这n点中任意一点向另外n-1个点的连线作垂线，则所有这些垂线的交点(不包括已知的n个点)的个数至多有______个．

(江苏省常熟市中学 查正开 215500)

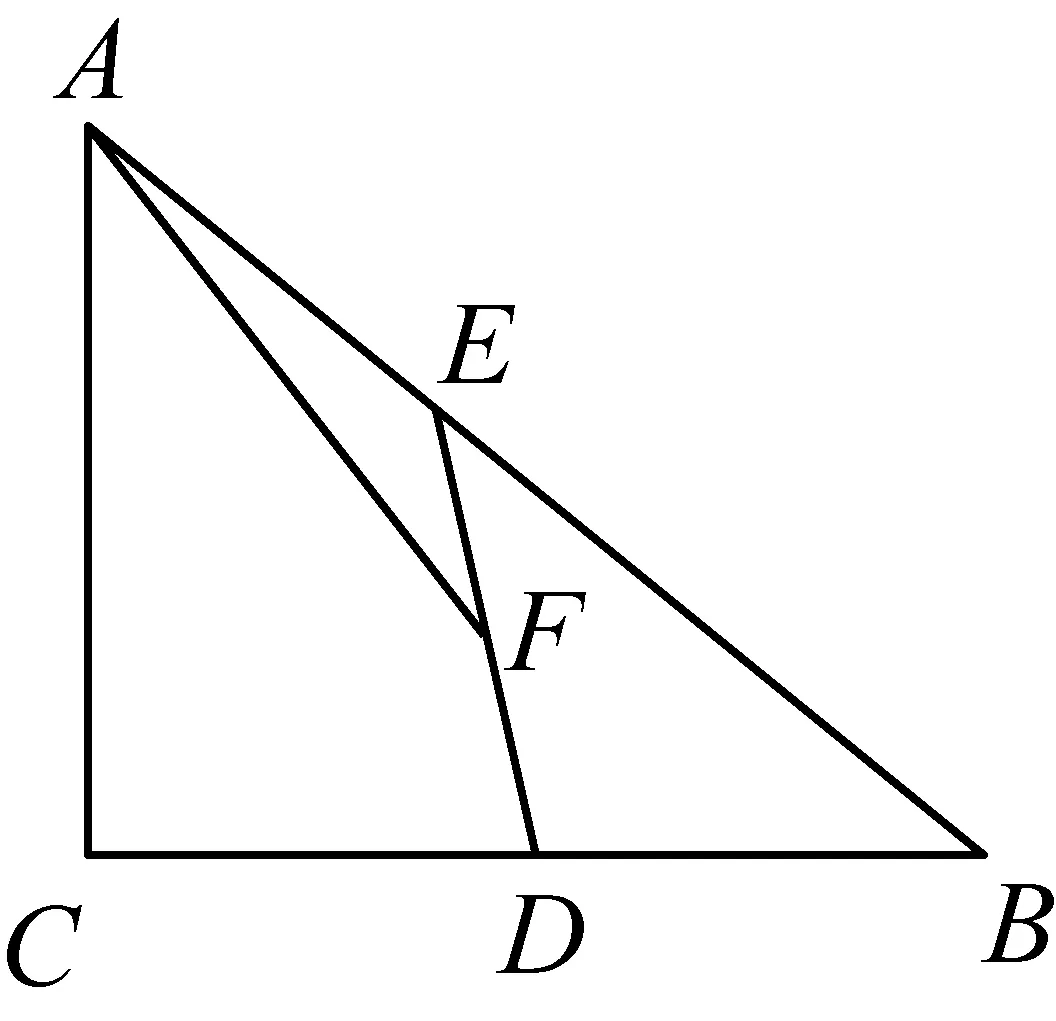
2617如图1，点A在⊙O上，点D在⊙O外，过点D作⊙O的割线DB2B1、DC2C1.连接AB1、AB2、AC1、AC2、AD，连接B1C1、B2C2分别与AD交于点E1、E2.

图1

(北京市朝阳区芳草地国际学校富力分校 郭文征 郭璋 100121)

证明如图2，设AD与⊙O相交于点F，连接FB1、FB2、FC1、FC2.

图2

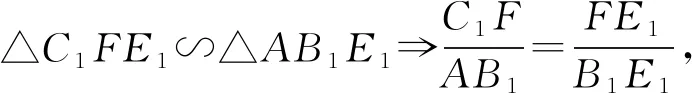
①

②

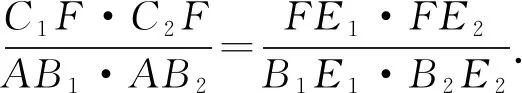
③

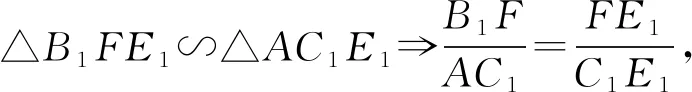
④

⑤

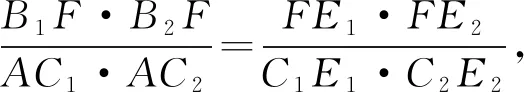
⑥

⑦

因为A、B1、B2、F四点共圆，

所以∠B2B1F=∠B2AF，即∠DB1F=∠DAB2.

又∠1为△DB1F和△DAB2的公共角，

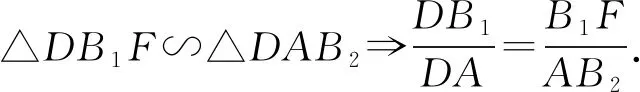
⑧

⑨

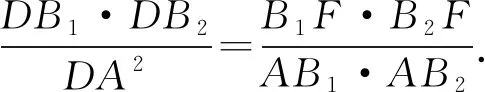
⑩

因为A、C1、C2、F四点共圆，

所以∠FAC2=∠FC1C2，即∠DAC2=∠DC1F.

又∠2为△DC1F和△DAC2的公共角，

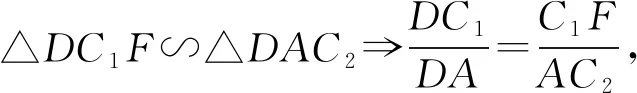
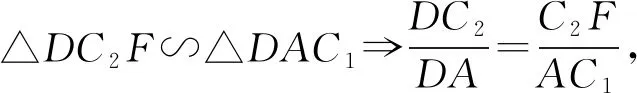
由圆的割线定理得DB1·DB2=DC1·DC2，

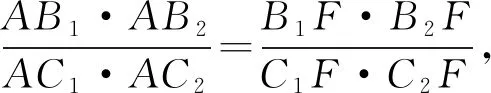
2618△ABC中，证明：

(2)4cosAcosBcosC-(sinA+sinB+sinC)2+(1+cosA+cosB+cosC)2=0；

(3)[-6-2(cosA+cosB+cosC)]·

(华中师范大学国家数字化学习工程技术研究中心 彭翕成430079； 江苏常州九章教育科技有限公司 曹洪洋213002)

证明设△ABC的外接圆半径为R，内切圆半径为r，半周长为p，

根据三角形面积关系和海伦公式可得

p2r2=p(p-a)(p-b)(p-c)，

即pr2=p3-p2(a+b+c)+p(ab+bc+ca)-abc

=-p3+p(ab+bc+ca)-4pRr，

可得ab+bc+ca=r2+p2+4Rr.

根据恒等式

cos2A+cos2B+cos2C+2cosAcosBcosC=1得

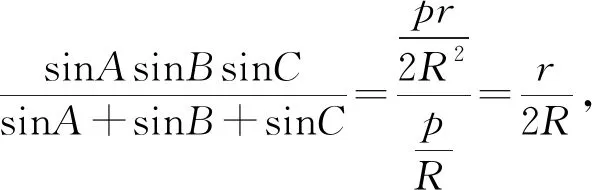
至此，只需将上述结论代入原式即可证明.

(安徽省枞阳县宏实中学 江保兵 246700)

证明首先在△ABC中，由三角形内切圆知识，有

设△A1A2A3,△A1A2A4,△A1A3A4,△A2A3A4的内切圆的半径分别为r4,r3,r2,r1，结合下图有

同理

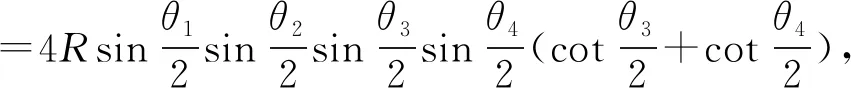
考虑到△ABC中的欧拉公式OI2=R2-2Rr，

所以

由于r1+r3=r2+r4,

2620已知a,b,c为正数,且abc=1, 求证:

a2+b2+c2+6≥3(a+b+c).

(湖北省宜都市一中 刘宜兵 廖全清 袁昌芹 443300 )

证明不妨设0

a2+b2+c2+6-3(a+b+c)

故a2+b2+c2+6≥3(a+b+c),

当且仅当a=b=c=1时等号成立.

2021年9月号问题

(来稿请注明出处——编者)

(山西省临县一中 李有贵 033200)

2622如图，四边形ABOC中，AB=AC，OB=BC=CO，∠A=80°，点M在BC上，满足∠CAM=20°．以O为圆心，OB为半径作圆交AM于Q，求证:∠QBC=10°．

(湖北省公安县第一中学 杨先义 434300)

2623设a≥b≥c≥0,a+b+c=3,求证:

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000)

2624在Rt△ABC中，点D为直角边BC的中点，点E在斜边AB上且满足AE=CD，点F为

线段ED的中点，证明：∠CAF= ∠DEB.

(河南辉县一中 贺基军 453600)

2625已知锐角△ABC，求

(安徽省六安第二中学 陶兴红 237005)