基于自由转子的纱线扭矩的检测方法

洪 焱，沈小林，田 野，吴三宝，杨 进

(1.武汉纺织大学 纺织新材料与先进加工技术省部共建国家重点实验室，湖北 武汉 430200；2.广东溢达纺织有限公司，广东 佛山 528000)

纺织面料的纬斜是衡量织物品质的重要指标[1]。目前，国内企业在实际生产中为减小面料的纬斜程度，一般通过蒸纱定形将纱线的扭应力减小到合理的范围内[2]。对不同种纱线蒸纱定形标准也不一样，由于无法准确得知每种纱线的扭矩，导致蒸纱前需要反复打样测试以确定其定形标准，不仅操作繁琐、效率较低而且存在一定误差。因此准确掌握纺织用纱线的扭矩在蒸纱定形中显得尤为重要。

现有的关于纱线扭矩的检测方法一般分为扭摆法和扭力秤法[3]。Zurek等[4]利用扭摆法测试了混纺纱的扭转性能，但此方法仅限于较小的扭应变和摆动周期，对有捻纱线的测试误差较大。Freston等[5]采用扭力秤法对小扭矩试样进行测试，结果发现该方法仅适用于无捻纱线或纤维的加捻测试，无法对已有捻度的纱线进行准确测量。因此，亟需一种经济、高效、便捷的方法来准确获取纱线的扭应力，对其做出准确区分以适用不同的蒸纱标准。

为此，本文研究设计了基于自由转子的纱线扭矩的检测装置来对纱线扭矩进行准确测量。通过该装置可准确得到纱线的扭矩，从而匹配准确的定形标准，减少后续织造织物发生纬斜而对品质造成不良影响。

1 检测系统的组成及其工作原理

1.1 检测系统

本文研究所开发的基于自由转子的纱线扭矩的检测系统主要由箱体、转轴、转子、光电门、电磁阻尼等部件组成，可自动采集纱线的测试信号并通过后续计算机处理得到测试纱线的扭矩。其中转子的要求最为精细，其详细结构如图1所示。该结构是由齿轮转盘、圆棒、穿纱孔、磁性金属片等构成。整个装置除磁性金属片以铁为材质外其余部件均为铝合金制造而成。转子底部为圆锥状，材质轻巧且转动时所受风阻较小，可保证其转动的稳定性。

齿轮圆盘共具有40根齿，每根齿之间均匀间隔9°，当齿从光电门中转过时，经红外扫描，其转过的角度与所用的时间便会以数据的形式传输到计算机中进行后续处理。

1.2 工作原理

上下两端分别与转轴、转子相连的纱线在系统底部电磁阻尼的作用下保持静止悬挂状态，并通过转轴调节至合适长度。光电门因其响应速度快、稳定性好、在完成非接触测量时的准确度和稳定性都很高，是用来收集测试信号的理想媒介[6]。转子在纱线自身扭力的作用下由静止开始平稳的转动，此时光电门将扫描齿轮圆盘所得到的数据传输到计算机中通过Origin加以处理，即可得到其角加速度与时间的关系曲线。从图上便可准确得到转子的初始角加速度。

由转子的初始角加速度和刚体绕定轴的转动定理，即可计算出纱线的扭矩[7]：

M=Iβ

(1)

式中：M为纱线的扭矩，N·m；I为转子的转动惯量,kg·m2；β为转子的角加速度,rad/s2。

2 转动惯量分析

转动惯量是刚体力学中比较重要的物理量，用来描述刚体在转动中惯性的大小[8]。通过检测系统可得到转子角加速度的数值，并计算出测试所用的转子的转动惯量，可获取最终所需的纱线的扭力值。

转子由圆锥底盘、齿轮圆盘、磁性金属片、带有穿纱孔的圆棒等4个部件组成。形状规则的匀质刚体转动惯量可直接从定义出发，通过积分计算其转动惯量[9]。由相加性原理，对同一转轴而言，刚体的总转动惯量等于各部分转动惯量之和[10]。可知，只需计算转子各部件的转动惯量，然后累加即可得到转子的转动惯量。

2.1 磁性金属片和圆棒的转动惯量

转子的磁性金属片部件在计算转动惯量时可将其视作一个匀质圆盘，因此该部件的转动惯量计算公式和圆棒部件一致，如式(2)所示[11]。

(2)

式中：I为刚体的转动惯量，kg·m2；m为刚体的质量,kg；r为刚体的半径,m。

将测量所得的磁性金属片和圆棒的质量m、半径r分别代入式(2)，得到磁性金属片的转动惯量为2.40×10-7kg·m2，圆棒转动惯量为 2.80×10-10kg·m2。

2.2 齿轮圆盘的转动惯量

齿轮圆盘的结构如图1所示，对于齿轮圆盘的转动惯量一般将其分为2部分：圆盘内圆和外部的三角形齿。

经过测量计算所得的齿轮圆盘的内圆半径r和质量m可得到齿轮圆盘内圆的转动惯量为1.52×10-7kg·m2。

对于圆盘外围的三角形齿，单个三角形齿相对质心的转动惯量[12]为

(3)

式中：I为刚体的转动惯量，kg·m2；m为三角形齿的质量，kg；a、b、c分别为三角形的三条边长，m。

将所测数据代入式(3)可得单个三角形齿相对质心的转动惯量为4.01×10-11kg·m2。根据转动惯量的平行轴定理可计算出三角形齿的转动惯量为[13]

Iz=Ic+md2

(4)

式中：Ic为刚体绕质心转动的转动惯量，kg·m2；m为刚体的质量，kg；d为2个转轴之间的距离，m。

由于三角形齿为等腰三角形，其质心在该三角形底边的高上，距顶点三分之二处，因此可得该质心到转盘中心的距离即2个转轴之间的距离，将其代入式(4)即可得到单个三角形齿的转动惯量为4.49×10-9kg·m2，因齿轮圆盘共有40根齿，因此齿的总转动惯量为1.80×10-7kg·m2。

将上述圆盘内圆和三角形齿的转动惯量相加得到最终所需的齿轮圆盘的转动惯量为3.32×10-7kg·m2。

2.3 圆锥底盘的转动惯量

连续质量分布的刚体，往往先取任一质量微元dm，然后利用密度这个中间量进行转化后求解[14]。

转子的圆锥底盘部件如图2所示，利用微元积分的方法求其转动惯量。将圆锥分为若干不同直径的薄圆盘，其中任一半径为r的圆盘与圆锥底部的距离为h，圆锥高为H，底部半径为R，通过计算最终得到圆锥部件的转动惯量如式(5)所示。

图2 圆锥底盘Fig.2 Cone chassis

(5)

式中：m2为圆锥底盘的质量，kg；R为圆锥底盘的底部半径，m。

将测量所得圆锥底盘质量和底部半径代入式(5)，得到圆锥底盘的转动惯量为8.88×10-8kg·m2。将上述得到的4个部件的转动惯量相加，得到最终所需转子的转动惯量为6.61×10-7kg·m2。

3 实验部分

为证明该方法的普适性以及准确性，采用不同类别纱线来验证纱线长度和捻度与扭矩之间的关系。其中白色单纱用以测试不同长度纱线的扭矩，蓝色单纱用以测试不同捻度纱线的扭矩。在纺织生产中同线密度纱线因其生产批次、仓库中存放的时间以及不同染色及后续处理过程的不同，会使其内部的扭应力出现不同程度的差异。企业需要对其作出区分并按照不同的蒸纱标准消除其内部扭应力。为证明该方法的实用性,采用各色29.2和19.4 tex的单纱用以测试同线密度不同颜色纱线的扭矩，以对其进行准确区分。每组测试均进行5次，取其平均值。

本实验以各类由广东溢达纺织有限公司提供的纯棉单纱为样品进行测试。样品纱线的各项参数如表1所示。

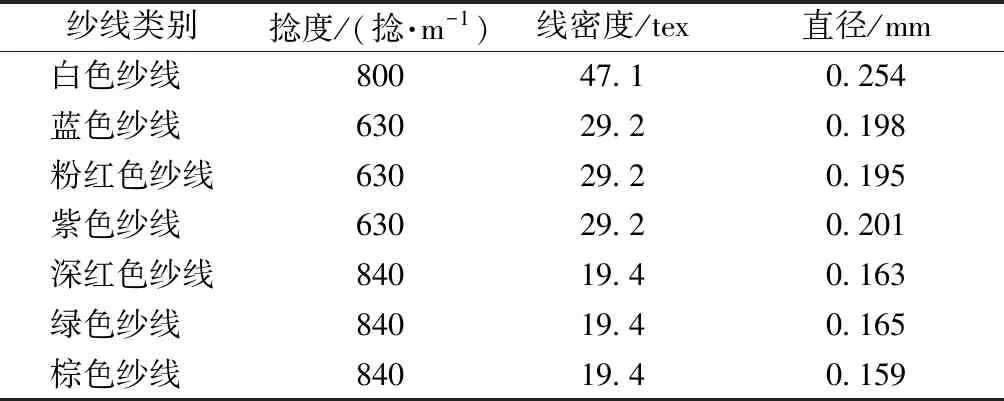
表1 样品纱线的参数Tab.1 Parameters of sample yarn

取800捻/m的白色纱线20 cm进行检测，可得到转子转过的角度、角速度和角加速度与时间的关系曲线如图3所示。

从图3可看出：转子在纱线扭力的作用下从静止开始转动，其转过的角度与时间呈正比关系，随着时间的增加，角度逐渐增大；随着时间的增加，转子的角速度先增加到1个峰值，然后逐渐下降；初始状态时，转子角速度为零，转子所受空气阻力为零，对所求初始值无影响；随着时间增加，转子角速度达到最大值，空气阻力与时间的二次方成正比，此时转子所受空气阻力最大，而此时纱线残余力矩已较小，低于转子所受的阻力导致了转子角速度开始降低。

图3 转子转过的角度、角速度和角加速度与时间的关系曲线Fig.3 Relationship curve between angle(a)，angular velocity(b)，angular acceleration(c)and time of rotor

其角加速度从最大值逐渐减少至零，这时转子角速度达到最大值，纱线的残余力矩较小，在空气阻力的作用下转子角加速度开始反向增大。可准确地得到测试纱线的初始角加速度为2.27 rad/s2。

利用式(1)和前面计算出的转子的转动惯量得出该纱线的扭矩为1.50×10-6N·m。

3.1 不同长度纱线的扭矩测试

由牛顿第二定理，物体的加速度与物体所受的外力F成正比，与物体的质量成反比。当纱线的长度即外力和质量成比例增加时，其角加速度的值不会变化，即所测纱线的扭矩为一个定值，与长度无关。为验证本文方法的准确性，依次再取长度为8、10、12、14、16、18和22 cm的白色纱线进行测试,每组纱线均测试5次取其平均值。将所得数据作图和计算处理之后得到的结果如表2所示。

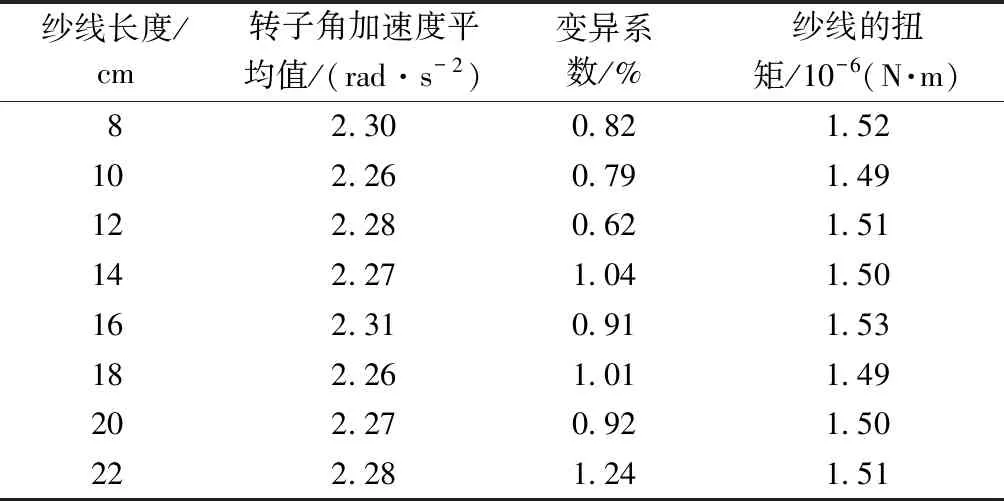
表2 不同长度纱线的测试数据Tab.2 Test data of different length yarns

从表2可以看出，对不同长度纱线进行测试之后所得的纱线的扭矩在误差范围内，均稳定在1.50×10-6N·m这一定值。

为使结果更具说服力，更换转子的磁性金属片，改变转子的转动惯量。新换金属片的半径为13.5 mm，质量为0.96 g，经计算其转动惯量为8.75×10-8kg·m2，则整个转子的转动惯量为5.09×10-7kg·m2。

取该纱线20 cm，于装置中进行测试，得到转子角加速度与时间的关系曲线如图4所示。从图可知该纱线的初始角加速度为2.99 rad/s2，由式(1)计算得到纱线的扭矩为1.52×10-6N·m，与前面测试所得数据在误差范围内完全相同。

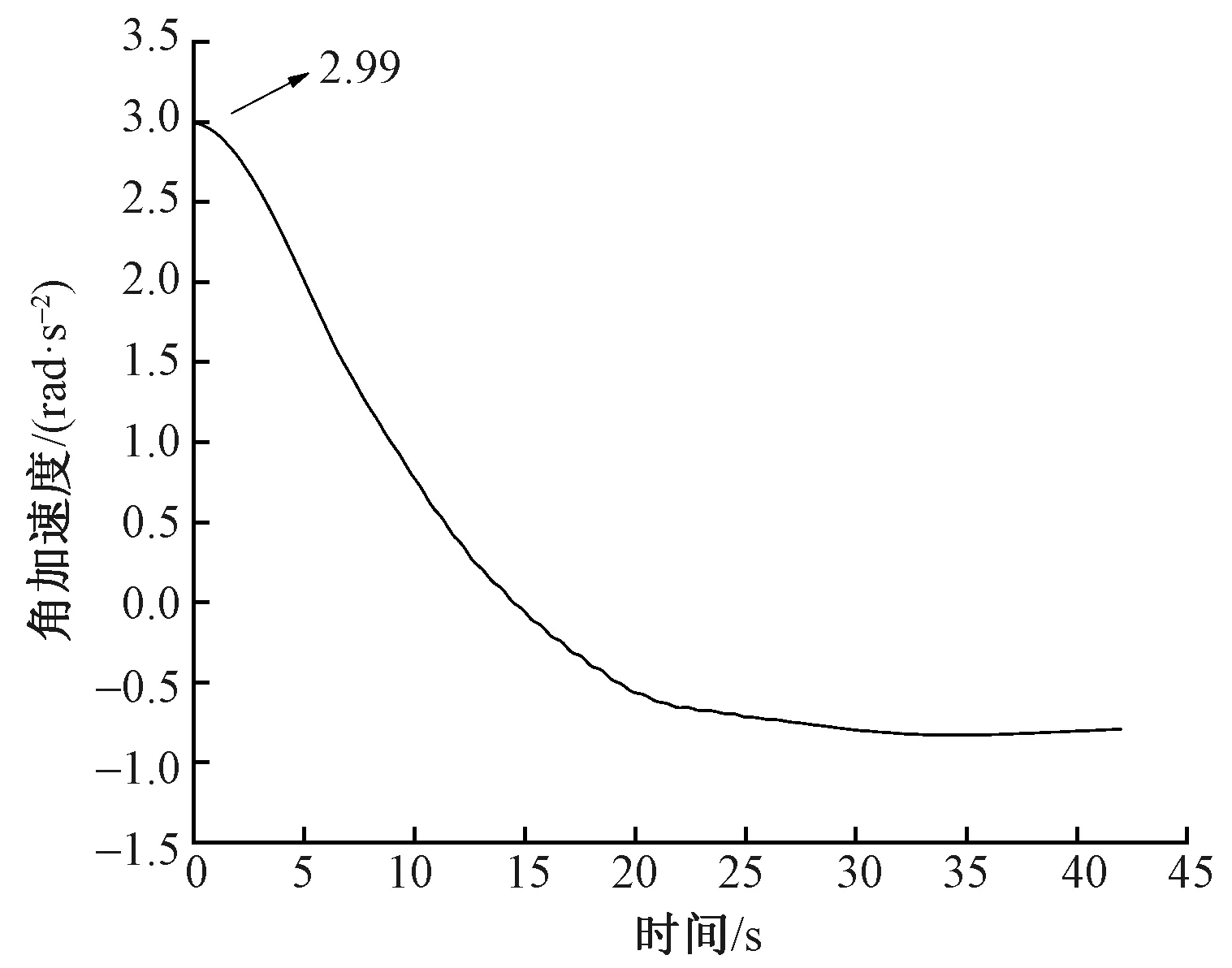
图4 转子的角加速度与时间的关系曲线Fig.4 Relationship curve between rotor angular acceleration and time

3.2 不同捻度纱线测试

为进一步验证测试装置的准确性，以630捻/m的29.2 tex蓝色纱线为样本，每次取15 cm对其进行加捻和解捻，以得到其不同捻度的测试数据,结果如表3所示。

表3 不同捻度纱线的测试数据Tab.3 Test data of yarns with different twist

为更清晰地得出不同捻度纱线与其扭矩之间的关系，以捻度为横坐标，扭矩为纵坐标作出关系曲线，如图5所示。

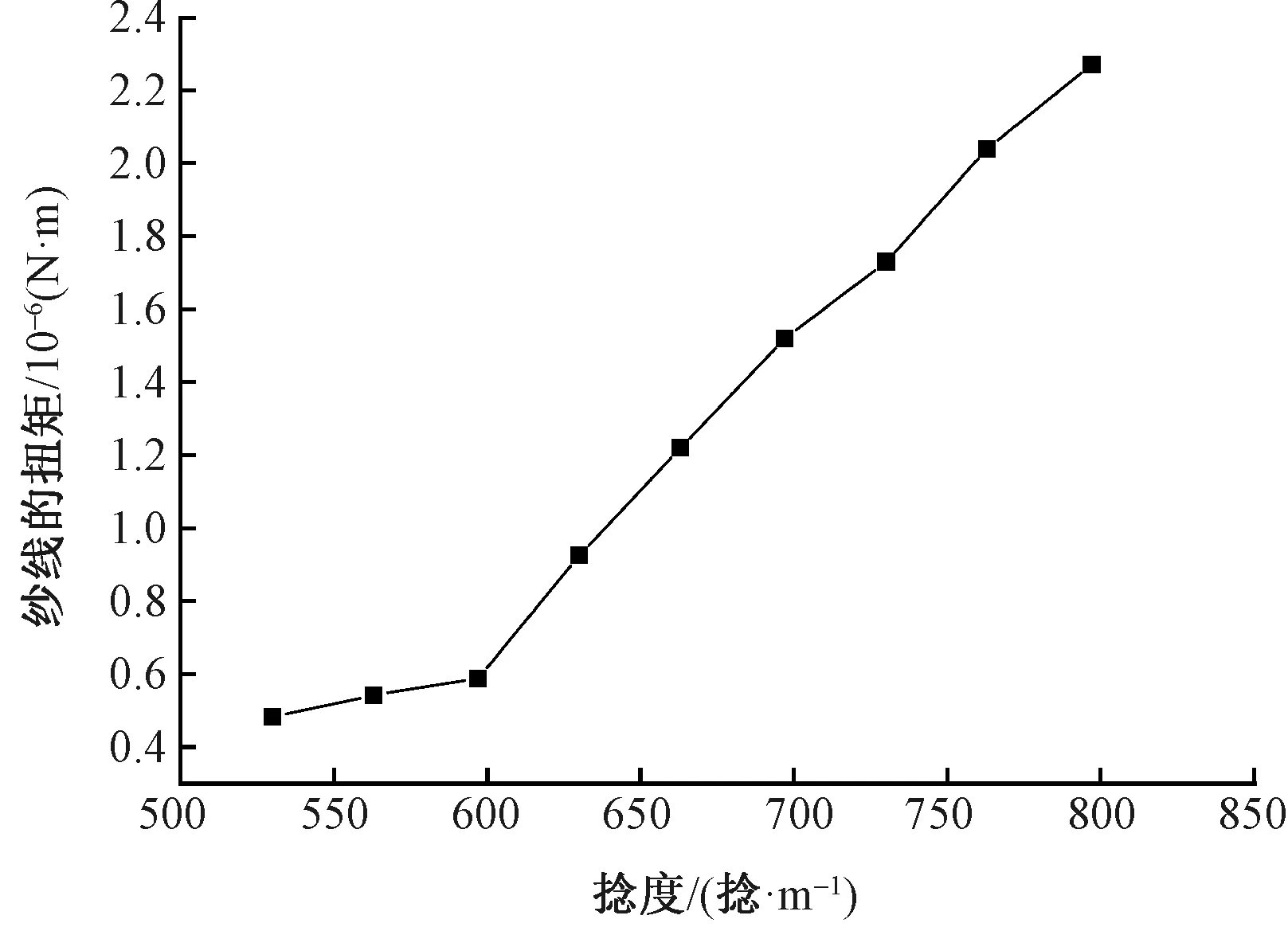
图5 不同加捻程度的纱线扭矩与捻度的关系曲线Fig.5 Relationship curve between yarn torque and twist for different twisting degrees

从理论分析，纱线的扭矩应与其捻度成线性关系，从图中可清晰看出，纱线在加捻段，不同捻度测试下的纱线扭矩与捻度在误差范围内呈现出线性关系，充分验证了本文测试方法的准确性。而在解捻段，由于纱线的放置时间导致的应力松弛以及空间位阻效应导致其呈现出非线性关系。

3.3 同线密度不同颜色纱线的测试

分别取同类型的29.2和19.4 tex经过不同染色和后续处理的纱线进行测试,所得结果如表4所示。

表4 同线密度不同颜色纱线的测试数据Tab.4 Test data of yarns with same linear density and different colors

工厂实际生产中同线密度纱线由于生产批次、存放时间以及不同染色以及后续处理，其纱线的扭矩也会出现不同程度的变化，导致其后续的蒸纱定形标准也会随之变化。从表4可以看出，相同线密度不同颜色纱线的扭矩之间存在明显的差别，证明本方法可对其作出准确区分，并按照不同的蒸纱标准消除其内部扭应力，在企业实际生产中具有重要的指导意义。

4 结 论

为实现对纱线的扭矩进行准确的测量，使其匹配准确的蒸纱定形标准，从而减小织物的纬斜概率，提出了基于自由转子的纱线扭矩的检测方法，并以此对多种纱线进行检测。结果表明，纱线的扭矩为一个定值，与测试所用纱线的长度无关，同种纱线其内部扭矩与捻度在误差允许的范围内呈现出线性关系。除此之外，对于不同扭矩的相同线密度纱线，本方法可以对其作出准确区分，并按照不同的蒸纱标准消除其内部扭矩，不仅在如今的纺织业生产检测中具有广阔的应用前景，而且为纱线扭矩领域的研究提供了一种新的思路。