基于哈密顿原理轴向运动纱线的振动特性研究

李 杨， 胡旭东， 彭来湖， 郑秋扬

(浙江理工大学 浙江省现代纺织装备技术重点实验室， 浙江 杭州 310018)

纱线是纤维沿轴向方向经加捻后形成的纤维集聚体，在织造过程中纱线受到外力作用时呈现极其复杂的动力学特征[1-2]。纱线在传输过程中的稳定性对织物的品质、生产效率以及后续加工的顺利进行产生较大影响[3]。在织造过程中纱线振动引起的张力变化，会使织物表面产生疏密不匀、高低不平等问题，影响产品质量，降低织物等级[4]。因此，对纱线传输过程中的振动特性分析显得尤为重要。

纱线轴向运动的横向振动可转化为运动弦线的非线性振动，很多学者对此进行了研究。Swope等[5]利用状态空间的复特征值确定弦的模态函数；Mote等[6]利用哈密顿Hamilton原理研究了轴向运动弦线的非线性振动特性；Ames等[7]采用Galerkin截断法讨论了纱线周期激励条件下的运动特性，建立了包含纱线速度、初始张力、横向位移和线密度的控制方程。随着研究的不断深入，以两端受约束的轴向运动纱线为研究对象，分析了主参激共振时系统的稳定性[8]；以纱线传输速度和初始张力作为因变量，对纱线的动态力学性能进行研究分析[9-10]。以往描述纱线大都为Lagrange范畴，而纱线运动模态较为复杂，基于此，本文采用哈密顿动力学方法，研究了针织纬编生产中运动纱线的横向振动。通过研究纱线输送速度和以纱线作为连续介质系统的Hamilton双变量的函数，并利用变分原理求解行进纱线的对偶方程，以期对行进纱线的特征值以及在不同传输速度下的自由振动和受迫振动提供研究思路。

1 针织纬编纱线动力学模型

针织纬编在生产过程中，纱线由于织机针筒的转动从纱筒上退绕，经过输纱器穿过导纱孔钩在织针上[11]。纱线在运动过程中受到针织机初始张力激励和织机机构产生的外部激励发生振动。这些激励会造成纱线张力不稳定，从而导致纱线输送状态产生变化。

图1 轴向运动纱线模型

对轴向运动纱线系统的各变量和参数做无量纲化如下：

(1)

式中：c0为瞬时速度，s为运动时间。

(2)

式中：Xi,η、uj,η分别为横向、纵向位移分量。

该点的无量纲张力为：

(3)

在物质坐标系下，纱线的Lagrange运动微分方程为

(4)

在绝对坐标系下，纱线的运动力学微分方程：

(5)

忽略纱线在空间中各方向的振动，纱线的自由振动微分方程为

uk,tt+2cuk,ηt+δ(uk,t+cuk,η)+

(6)

式中：qk(t)为纱线受到的外部激励减去纱线静止状态下受到的载荷。

此时，初始条件和边界条件为

(7)

式中：αk(η)为纱线静止状态时位移构形；βk(η)为织机运转时纱线速度构形。

2 纱线振动模态函数

为方便求解，假设纱线在运动过程中所受阻尼为0，由式(6)得纱线的自由振动微分方程为

(8)

式中：U=U(η,t)为纱线上一点处于静止状态时的横向位移。边界和初始条件为：

(9)

绝对坐标系下纱线的无量纲Hamiltion函数为

(10)

引入U(η,t)的对偶变量p=p(η,t)。根据变分原理，得到Hamilton对偶方程组为

(U(η,t),p(η,t))T

(11)

用分离变量法得出对偶方程组(11)的特征值：

(12)

式中：Φ(η)=(Φ1(η)，Φ2(η))T是特征向量；λ为特征值。

纱线在静止时自由振动的特征值为

(13)

(14)

3 轴向行进纱线振动响应

3.1 轴向行进纱线自由振动响应

针织生产过程中纱线的输送状态会随着编织工艺的改变而发生变化。当纱线轴向行进速度为0时，由于自身重力会产生自由振动。根据展开定理，纱线的横向位移函数可表示为模态函数的叠加，即：

(15)

初始条件为

(16)

式中：

(17)

根据式(14)纱线振动的辛共轭正交性条件，可得到纱线轴向行进速度为0时的自由振动响应：

(18)

3.2 轴向行进纱线受迫振动响应

假设织机在运行过程中由各机构振动对纱线产生的耦合激励为均匀激励，纱线受迫振动的动力学方程为

(19)

式中：f(η,t)为作用在纱线上的载荷。纱线受迫振动的对偶方程为

(20)

展开全状态向量：

(21)

把纱线所受外部激励函数h按照特征向量展开为

(22)

将纱线振动对偶方程的展开全向量(22)和纱线外部激励函数的特征向量代入纱线受迫振动的对偶方程(20)，得：

(23)

对于纱线的受迫振动，我们只考虑f(η,t)的第1项，得到纱线系统受迫振动的特解：

(24)

4 数值分析和讨论

为验证本文主要结果，以棉纱为例，初始张力T=120 cN、弹性模量E=7.84 MPa、长度S=1.2 m、线密度ρ=27.4 tex，进行了数值模拟。通过算例分析了纱线不同速度下的模态，指出速度对模态的形状和幅值的影响。此外，还讨论了纱线的自由振动响应以及受迫振动响应。

4.1 纱线临界速度响应

考虑纱线自由振动模态的前三阶正交归一化模态函数，我们对纱线在不同行进速度下的模态进行分析，指出行进速度对模态的形状和振动幅值的影响。

图2示出c=0.8,c0=1时的前三阶模态函数。可以看出随着行进速度的增大，模态实部幅值的绝对值随之减小。反之，随着行进速度的增大，模态虚部的幅值的绝对值随之增大。

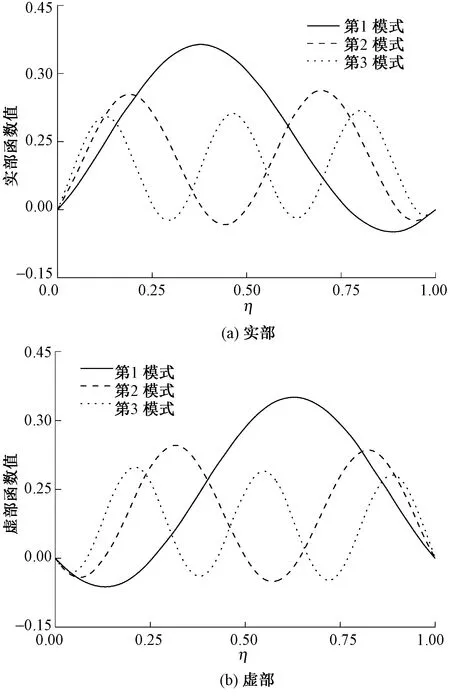
图2 行进速度接近临界速度时模态函数

为观察纱线运动速度对模态的影响，以3种不同的速度c=0.0,c=0.5,c=1.0计算模态函数的实部。图3示出不同运动速度下纱线的前三阶模态实部函数。可以看出模态函数的形状与纱线的速度密切相关。纱线运动速度与模态函数的实部呈正相关关系。反之，纱线运动速度与前三阶模态函数的周期为负相关关系。

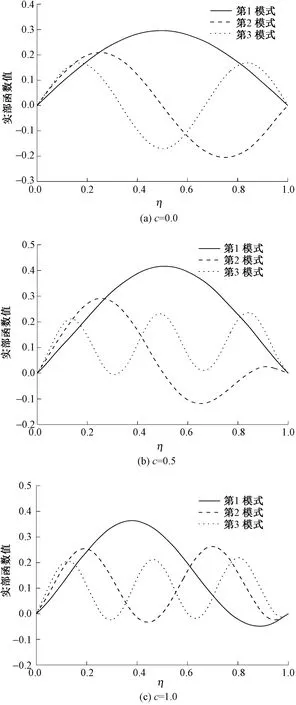
图3 不同速度下模态函数

4.2 纱线自由振动响应

在计算纱线的自由振动时，设初始速度为0，初始构形U=0.3η(η-1)。图4示出纱线中间位置处c0=0.5时不同行进速度下的响应曲线，随着行进速度c的增大纱线振动得响应周期变大。图5示出纱线在不同位置处的响应曲线。随着η的增大，响应幅值逐渐增大，并且在中点处达到最大。

图4 不同行进速度的响应

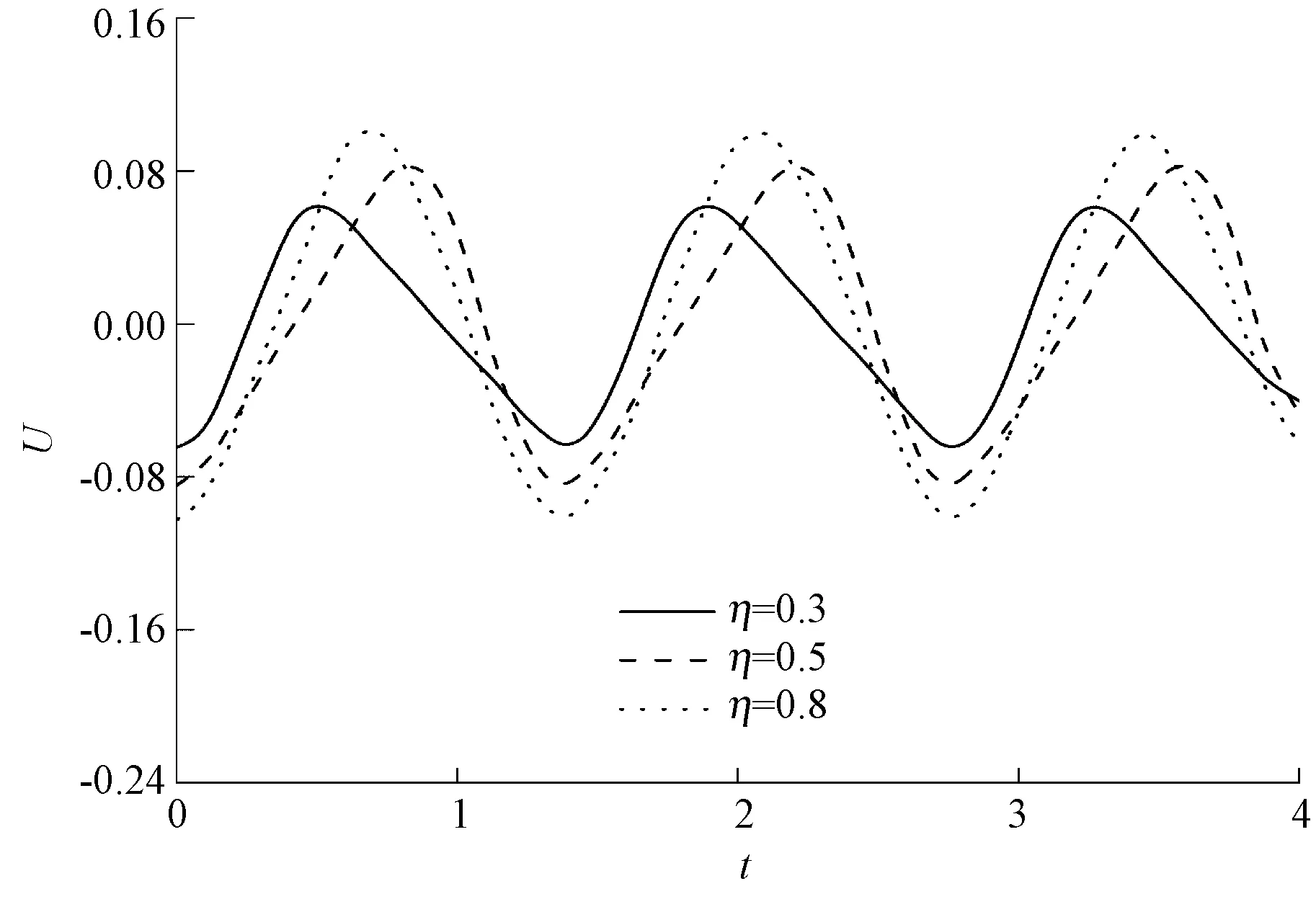
图5 不同位置的响应

4.3 纱线受迫振动响应

考虑无阻尼时纱线受迫振动，对一个周期内不同外激频率、不同传输速度和不同项数构形的影响。

图6示出纱线中点位置处c=0.5,c0=1.8时一个周期内的构形，可看出构形的幅值随着时间的增大而减小。图7示出为c=0.5,c0=1.8时纱线在不同运动速度时的构形，可看出运动速度越大构形幅值变化越大，周期变小。图8示出c=0.5,c0=1.8,t=1.2时，取不同项数的模态函数叠加得到的构形，n=2,n=3在时构形基本重合，因此取前2项模态函数叠加即可计算出纱线横向位移的大小。

图6 一个周期内构形图

图7 不同行进速度下的构形图

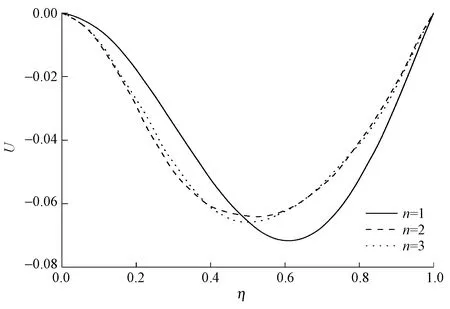
图8 不同项数构形图

5 结 论

本文以针织纬编织机为例，建立了由储纱器到织针导纱孔之间的运动纱线在Hamiltonian体系下的动力学微分方程，引入纱线横向位移的对偶变量，利用变分原理，得到行进纱线的对偶方程组。根据分离变量法，求得纱线振动的特征值和特征向量。利用辛共扼正交性条件和展开定理，得到了纱线自由振动响应。通过有关算例求解并分析了纱线的模态。经数值仿真可知，纱线的传输速度不同，振动响应周期也不同，速度越大响应周期也越大；运动速度不变，纱线上不同点的响应幅值不同，纱线中点处的振幅最大，两边逐渐减小；在1个振动周期内，纱线振幅在起始时刻振幅最大，而后逐渐减小；纱线振动位移按模态展开项数n=2,n=3时的构形基本相同，只取前2项相即可计算出纱线的横向位移。