分级随机采样弱随机RRT算法及在移动机器人运动规划中的应用

郑 维，张 涛，王洪斌，田亚静，王洪瑞

(1.燕山大学 电气工程学院，河北 秦皇岛 066004；2.国网石家庄市藁城区供电公司， 河北 石家庄 052160; 3.河北大学 电子信息工程学院，河北 保定 071000)

1 引 言

自主机器人的运动规划一直是热门的研究领域，其目的是为机器人在空间中规划出一条带有控制序列的运动轨迹，使机器人能够完成给定的运动行为。实现运动规划的方法主要有两类：基于图论的方法[1,2]和基于采样的方法。基于采样的规划方法避免了显式的构造构型空间，从而避免了“维度灾难”问题，首先从状态空间中随机抽取样本，然后检查样本的可行性，并选择接受或拒绝该样本。快速扩展随机树(rapidl expansion random tree,RRT)算法以其简单高效的算法流程以及概率完备性的特点，在基于采样的规划方法中有较大优势。

1998年，Lavalle S M[3]首先提出RRT算法;文献[4]严格地分析随机采样算法返回的解的代价随样本数量的增加的渐近行为；文献[5]针对动态环境，提出了一种基于采样算法的实时动态规划框架；文献[6]在RRT算法的基础上，提出了一种基于增量采样的运动规划算法，解决了集群环境下的近似最优运动规划问题；文献[7]结合方向相似性得多步扩展与贝塞尔曲线拟合生成初始解；文献[8]提出了基于“懒惰”的最优快速探索随机树算法，能够在静态和动态环境中使用更新的信息进行实时重新规划；文献[9]引入自适应引力场以获取采样点，加快算法得收敛速度；文献[10]提出了一种渐进优化的采样算法，得到初始路径后划定子区域进行重接线，从而得到最优路径；文献[11]提出了Informed RRT*-Connect算法，在获取初始解后进行重新抽样，并仅接受更好的解，以此获取最终解；文献[12]使用双树搜索以加快搜索速度，获取初始解后，对双树进行知情采样，优化初始解；文献[13]根据人工势场法建立的势场进行采样，并使两棵树同时向前推进，直至相交,减少算法的迭代次数；文献[14]引入了回归机制，以防止过度搜索配置空间，提升算法规划的成功率；文献[15]所提出的算法中，采样节点是由目标偏差采样策略以可变概率确定的，可以在不同障碍物密度的区域中平衡搜索时间和安全性；文献[16]使用神经网络来预测成本函数，并设计了一种新的随机搜索树重构方法，以在配置空间中寻找接近最优的解决方案；文献[17]结合了P-RRT*和Q-RRT*的优势，确保快速收敛到最佳解决方案，并生成更好的初始解决方案；文献[18]扩大了节点可能存在的父节点集合，从而生成更好的初始解；文献[19]采用了更集中地偏向RRT树形增长的方法，加快了算法的收敛速度；文献[20]结合双树结构提出了一种RRT*的新颖方法，以分离扩展和优化过程；文献[21]引入了双向变体和启发式搜索，提高了收敛速度，并具有更高的内存利用率；文献[22]提出自适应混合动态步长和目标吸引力RRT，在缩短路径的长度的同时加快了算法的求解速度。

基于上述研究内容可知，尽管加快算法求解速度，减少算法迭代次数已经成为RRT算法改进的重点，但大多数工作仍然是针对多树搜索及减少迭代次数等方面进行的，而造成RRT算法求解速度慢的根本原因在于其扩展时进行的遍历寻找最近节点所产生的大量计算。

针对移动机器人运动规划过程中，RRT算法采样效率低，寻找最近邻节点计算量大和非线性反馈控制器不受系统模型动态约束等问题，提出一种新的基于分级随机采样与扩展的RRT算法，同时设计了新的快速限幅反馈控制器。最后，使用3种不同类型的地图对移动机器人的运动规划过程进行仿真验证。结果表明：本文方法有效地缩短了RRT算法迭代后期遍历寻找临近节点的消耗时间，提高了系统的收敛速度，同时保证运动规划过程中反馈控制器能够始终满足系统模型动态约束。

2 RRT算法

RRT算法迭代完成树结构示意图如图1所示。

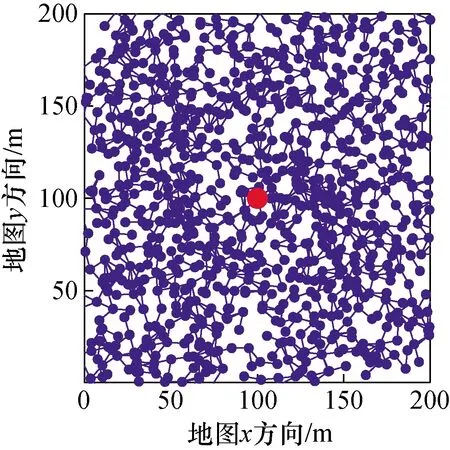
图1 RRT算法迭代完成树结构示意图Fig.1 Schematic diagram of the iteration completion tree for the RRT algorithm

随机树结构初始化为

T=[ni|i=1,2,3,…,N]

(1)

式中：ni=(x,y,qparent)∈χfree表示节点,(x,y)表示ni节点的坐标，qparent表示ni节点的父节点。

ni是直接从配置空间中随机选取，采用实值函数ρ:χ×χ→[0,∞)计算配置空间χ中点对点的距离来寻找ni最近的节点qnearest。采用碰撞检测函数判断自由空间χfree中是否存在xi；设D表示碰撞检测函数输出结果，当D为true时，表示χfree中存在xi，当D为false时，表示χobs中不存在xi，结束循环，进行下一次采样与检测。采用碰撞检测函数判断xi是否位于自由空间χfree中；当D为true时，表示xi处在χfree中，当D为false时，表示xi位于χobs中，结束循环，进行下一次采样与检测。

经过分析可得出：

(1)节点ni所携带的信息仅仅包含坐标与父节点之间的信息，并未携带更多有利信息，如当前节点与障碍物的相对关系、该区域节点数量、与目标区域的相对距离等。

(2)新节点是通过在配置空间χ中均匀采样得到的，当配置空间中存在大量的采样点时，才能保证采样点在配置空间中的覆盖率趋于1。但是如果T中存在大量的节点，尤其是在计算配置空间中点对点之间的距离时，会导致计算量激增。

(3)在RRT算法中，碰撞检测函数与搜索父节点的过程都要通过实值函数ρ:χ×χ→[0,∞)来获得距离参数。将新的采样节点连接到树中时需要遍历采样节点与树中节点之间的距离，获取最近节点作为父节点。随着迭代次数n不断增加时，执行该函数的次数呈指数型增长，从而导致计算量增加。

3 分级随机采样弱随机RRT算法

本文提出了一种新的基于分级随机采样与扩展的弱随机快速搜索随机树(RRT)算法，同时设计快速限幅非线性反馈控制器，在保证概率完备性的同时提高算法在迭代后期的搜索速度，进而提高算法在面对狭窄空间的搜索效率。

3.1 分级随机采样

针对RRT算法中由于均匀采样引起的采样结果不确定性问题，本文采用分级随机选取的采样方法，在保证概率完备性的同时减弱采样点的随机性，弱随机树结构初始化为

(2)

式中：先选择树中一节点作为子节点的父节点,priority_1,priority_2表示候选扩展节点集合；score_ni表示T中ni节点分数；a，b，c表示划分不同优先级的分数节点；else表示节点不作为候选扩展节点。

比较公式(1)和公式(2)，本文提出的算法将T中节点ni按照节点分数划分为不同的扩展优先级，priority_0,priority_1,priority_2。同时保证在划分优先级时T中节点ni最多只能存在于一个优先级集合中。

与RRT算法相比，本文提出的方法进行扩展时，并不是先选择随机点再寻找其父节点，而是先分级随机选取树中父节点作为待扩展的节点，再弱随机选择子节点的扩展方向，最后通过计算确定子节点的位置坐标。在选取待扩展父节点时遵循分级随机选取的原则，即若高优先级集合不为空，则在高优先级集合内随机选取待扩展节点，若高优先级集合为空，则判断中优先级集合是否为空。需要说明的是，每次迭代后更新待扩展点集合，当出现高中低3个优先级集合全部为空的情况，则表示此时采样点已经在状态空间中均匀分布，无需再次进行随机扩展，else集合中的节点不作为待扩展节点的候选节点。

为了使选取的待扩展节点能够顺利的完成扩展任务，本文为随机树中的节点预分配了8个扩展方向：上、下、左、右、左上、右上、左下、右下。每个节点不再作为质点进行空间搜索，而是存在一定的搜索范围，搜索范围是以每个节点为中心，半径为1/2R(R为步长值)的区域。与RRT算法相比，上述搜索方法提高了搜索效率。然而预分配的扩展方向并不全是可以扩展的，为了记录节点扩展方向是否可以扩展，本文采用2×4维矩阵dir_mat记录扩展方向，定义如下：

(3)

式中：dir_mat表示节点的方向属性矩阵，矩阵元素1，2，3，4，5，6，7，8分别对应节点的8个扩展方向，不可扩展的方向包括两种情况，第1种是位于障碍物边界或地图边界的节点，第2种是节点附近已存在节点。

方向属性矩阵与节点方向的对应关系如图2所示。

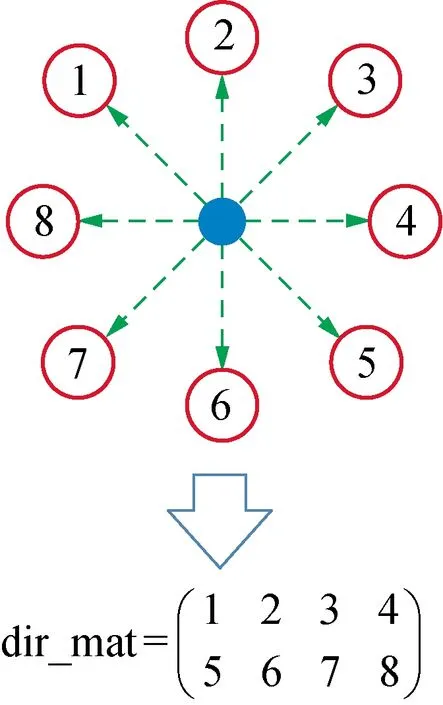
图2 方向属性矩阵与节点方向对应关系Fig.2 Correspondence of direction attribute matrix and nodes direction

3.2 获取子节点

为了获取子节点，计算出各子节点的坐标，给出子节点的计算公式如下：

(4)

式中：ni_childj,j=1,2,3,…,8表示ni节点各方向子节点；x、y分别表示节点横纵坐标；R为步长值。

依照待扩展集合优先级，优先在高优先级的扩展节点集合中随机选取ni节点，确定ni的dir_mat属性矩阵，随机选取子节点的扩展方向，两次随机选取保证探索方向的随机性。图3给出ni节点方向子节点示意图。

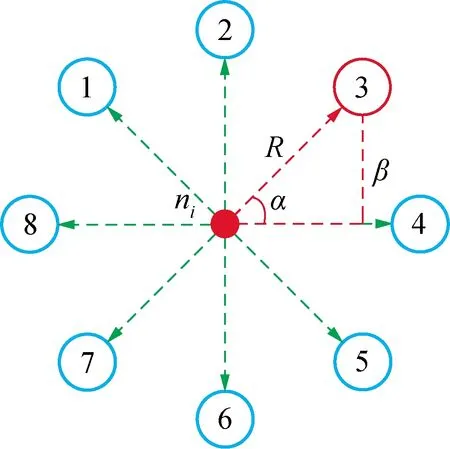
图3 ni各个方向子节点示意图Fig.3 Schematic diagram of the sub nodes in all directions for ni

图3中ni节点可扩展的8个方向，ni节点坐标为(x,y)，步长值设置为R，α=45°，β=R·sinα进而根据公式(4)计算出各个子节点的坐标。

3.3 搜索临近节点

在搜索临近节点的过程中，由于子节点qchild方向的弱随机性，会出现两种临近节点过度搜索的现象，如图4所示。

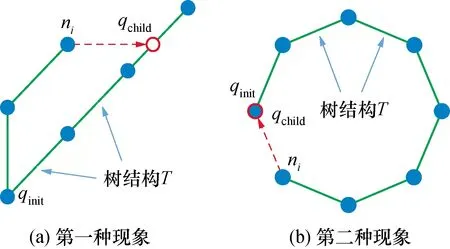
图4 临近节点过度搜索示意图Fig.4 Schematic diagram of the excessive search for the adjacent nodes

为了解决上述问题，本文对生成的qchild点进行临近搜索判断，同时为了避免大量的距离计算，提出一种新的判断策略，将距离计算问题转变为判断qchild邻域矩阵是否为0阵的问题，步骤如下：

第1步：初始化阶段，将与地图匹配的节点位置矩阵map_array初始化为0阵。

第2步：进行重复点判断时，选择合适的邻域矩阵半径，获取以qchild点为中心的邻域矩阵。

第3步：判断qchild的邻域矩阵是否为0阵，若为0阵，表示qchild点附近不存在节点，返回0，若不为0阵，表示qchild点附近已经存在节点，则不返回0。

第4步：成功扩展子节点后，更新节点位置矩阵map_array。

3.4 弱随机RRT算法

弱随机RRT算法具体步骤如下：

第1步：程序开始时，对程序进行初始化，包括树的结构体与节点位置矩阵map_array。

第2步：依据节点待选集合的优先级，选取待扩展节点qparent。

第3步：查找待扩展节点的方向矩阵，随机选择待扩展节点qparent的可扩展的方向。

第4步：依照公式(3)，计算子节点qchild的位置，并对qchild进行临近搜索判断。若qchild附近没有已存在的节点，则进行第5步，相反则返回第2步。

第5步：更新节点的待选集合与节点位置矩阵map_array

第6步：将子节点添加到树的结构体中。判断子节点是否位于目标区域，若位于目标区域，停止迭代，若子节点仍然位于目标区域之外，返回第2步。

图5表示分级随机采样弱随机RRT算法迭代示意图，从图中可以看出：采用分级随机采样弱随机RRT算法进行空间搜索，能够以较少的点探索到更多的区域，并且节点在空间中的分布均匀。

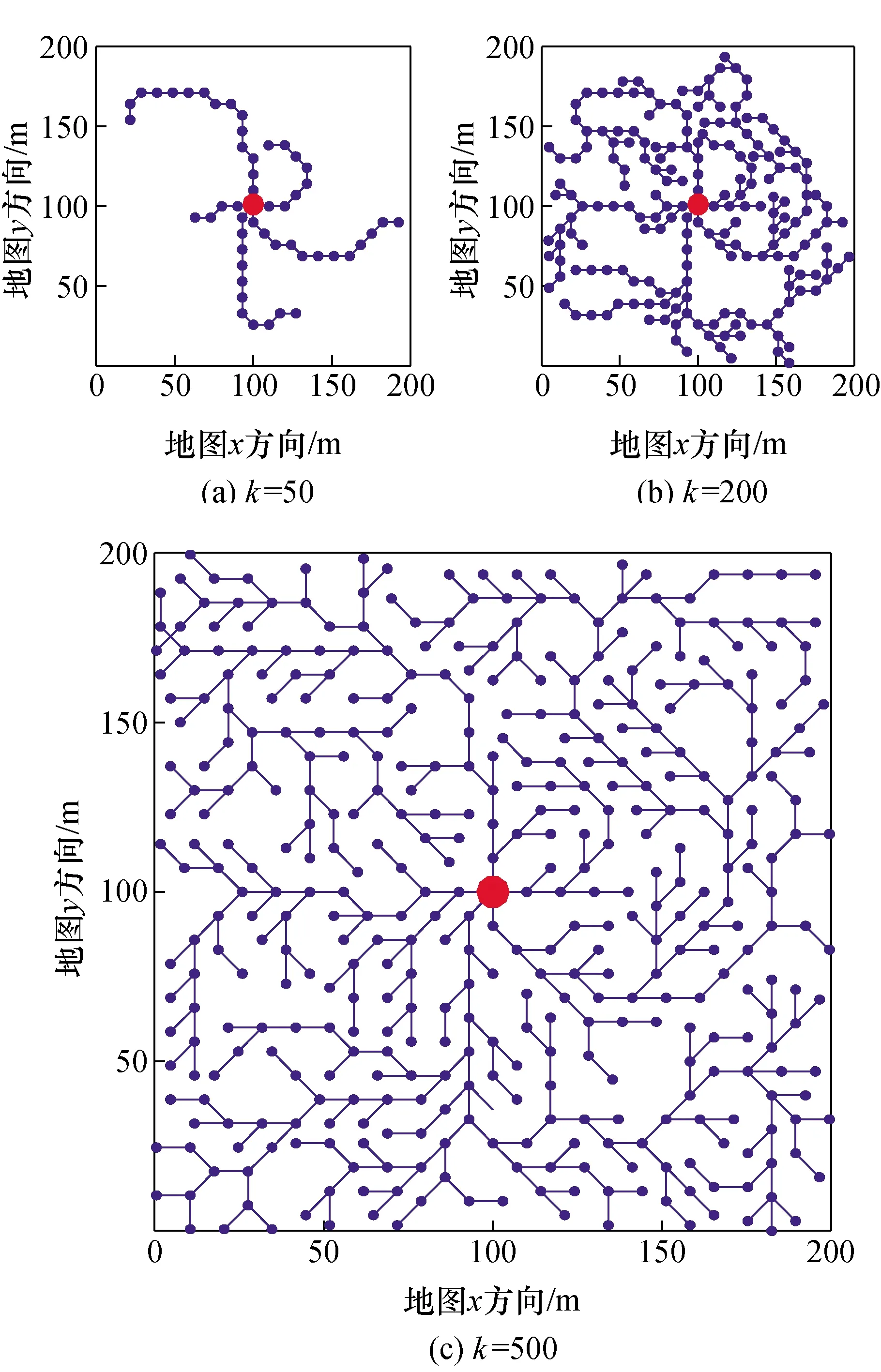
图5 分级随机采样弱随机RRT算法迭代示意图Fig.5 Iteration schematic diagram of hierarchical random sampling weak random RRT algorithm

图5(a)中迭代次数k=50，说明在迭代初期，新算法中树结构向着未探索空间进行搜索。

图5(b)中迭代次数k=200，说明在迭代中期，新算法能够使用较少的点探索到较大的区域，如果地图中障碍物较少，则此时能够获得初始解。

图5(c)中迭代次数k=500，说明在迭代后期，绝大部分空间均被探索，此时树中节点进入临近饱和状态。

图6表示分级随机采样弱随机RRT算法与RRT算法迭代次数与时间对比图。从图中可以看出当算法在迭代次数小于400时，两个算法消耗时间相差不大，但是随着迭代次数的增加，RRT算法消耗的时间要远远超出分级随机采样弱随机RRT算法消耗的时间。这是因为当随机点均匀分布在配置空间中时，分级随机采样弱随机RRT算法待扩展点集合均为空，即使继续迭代也不会再增加新的节点，缩短了消耗时间。

图6 分级随机采样弱随机RRT算法与传统RRT 算法迭代次数与时间对比图Fig.6 Comparison results of the iteration times and time between hierarchical random sampling weak random RRT algorithm and RRT algorithm

综上所述，本文提出的基于分级随机采样的弱随机RRT算法在降低了节点搜索过程中的时间消耗，与RRT算法相比，具有一定的优越性。

4 快速限幅非线性反馈控制器设计

文献[23]基于非线性反馈控制器，提出了跨越多个路径点时保持匀速来优化运动轨迹的方法。该方法可生成平滑的运动轨迹，且计算量低。非线性反馈控制器利用运动学模型可以引导机器人通过特定的路径点从起点移动到终点，但存在不受系统模型动态约束的问题，故不能保证机器人的速度、加速度严格满足机器人动态特性。针对上述问题，本文以差速轮式移动机器人为应用对象，采用分级随机采样弱随机RRT算法，设计快速限幅非线性反馈控制器，保证机器人在运动规划过程中满足物理模型的动态约束。

4.1 非线性反馈控制器

差速轮式移动机器人模型如图7所示，该机器人通过调节两个动力轮的加速度控制两动力轮的速度，实现机器人的前进、后退，左右转向等运动状态。该差速轮式移动机器人的运动学模型如下：

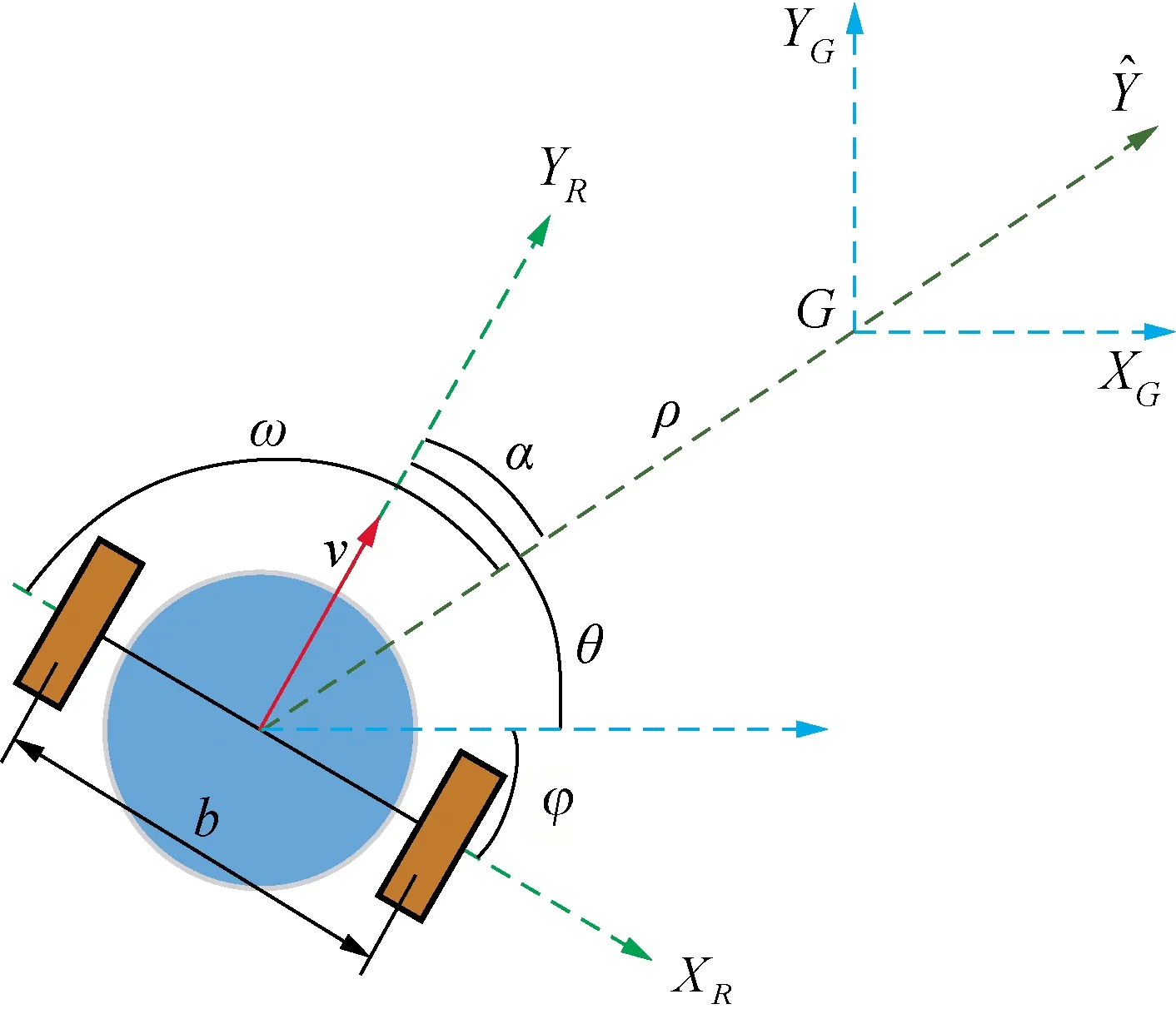
图7 差动轮式移动机器人模型Fig.7 Model of the differential wheeled mobile robot

(5)

基于上述模型，设计非线性反馈控制器如下：

(6)

为了保证机器人运动的稳定性，非线性反馈控制器应满足以下条件[23]:

(7)

由公式(6)可知，在运动开始时，由于机器人位于初始位置，故此时ρ为最大值，导致机器人的水平速度v在下一时刻瞬间达到速度最大值。然而移动机器人的水平速度受其水平加速度的约束，所以会出现机器人在起始时刻摆脱其物理模型约束的行为。对于这一问题，本文提出了将控制器中的平移速度与角速度作为机器人当前期望速度方法，并考虑机器人的物理模型约束[24]，机器人的实际平移速度与角速度关系如下:

v=v0+aΔt,ω=ω0+ΩΔt

(8)

式中：v0表示机器人当前时刻速度；a表示机器人当前时刻水平加速度；ω0表示为机器人当前时刻角速度；Ω表示为机器人当前时刻角加速度；Δt表示控制序列时间间隔。进而计算平移加速度a(t)：

(9)

式中：amax表示机器人最大水平加速度；v(t)表示机器人t时刻水平速度；vref(t)=Kρtanh (Kvρ(t))。

同理可以得到角加速度Ω，如下

(10)

式中：Ωmax表示机器人最大角加速度；ω(t)表示机器人t时刻角速度；ωref(t)=Kαα(t)+Kφφ(t)。

非线性反馈控制器虽然考虑了移动机器人的运动学动态约束，即移动机器人的平移速度与角速度均受其对应的加速度影响，却忽视了移动机器人的运动状态受两差速轮运动状态的因素[24,25]。两个动力轮在运动过程中会出现加速度大于最大加速度，从而使机器人摆脱其物理模型约束的情况。基于上述问题，考虑两个动力轮的加速度变化，使移动机器人的运动更加接近于真实环境中的运动状态，同时对控制器进行限幅处理,进而设计了快速限幅非线性反馈控制器。

4.2 快速限幅非线性反馈控制器

采用文献[25]中将控制器得到的平移速度与角速度作为期望值，考虑差速移动机器人的平移速度公式与角速度公式。

(11)

式中：vr、vl分别表示移动机器人右轮和左轮速度；b表示两差速轮之间的轮距。

已知平移速度v与角速度ω，计算可得到两个差速轮的速度vr和vl：

(12)

由控制器可得到移动机器人期望平移速度与期望角速度，再根据式(12)进一步得到移动机器人差速轮的期望速度。进而计算差速轮期望加速度：

(13)

式中：ar、al分别表示右轮和左轮加速度；vr_old，vl_old分别表示右轮和左轮上一时刻速度。

移动机器人在运动的起始时刻速度与角速度均为零，而期望的速度与角速度较大，会导致移动机器人的差速轮加速度超出最大加速度amax，所以需要对差速轮的加速度进行限幅处理：

(14)

若根据公式(14)对差速轮的加速度进行限幅，在移动机器人运动伊始，ar与al均大于amax，但是由于角加速度的存在，即ar≠al,而通过公式(14)进行限幅后会导致ar=al=amax，从而使角加速度为零，会使移动机器人的角速度无法收敛到目标角速度。由于存在上述问题，对加速度进行归一化后限幅：

(15)

通过式(15)对差速轮的加速度进行限幅处理，可在保证角加速度的同时确保差速轮满足移动机器人的运动学动态约束。此外，快速限幅非线性反馈控制律同样保证了机器人有平滑的全向运动轨迹，见图8。

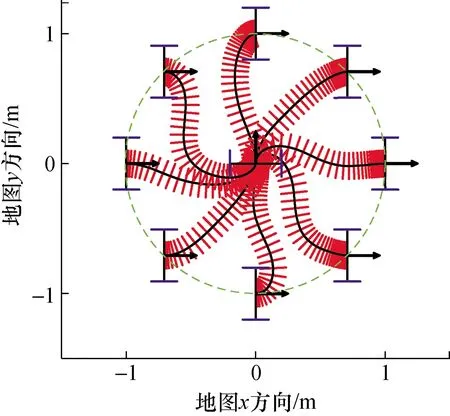
图8 移动机器人全向运动轨迹Fig.8 Omnidirectional motion trajectory of the mobile robot

5 仿 真

5.1 机器人运动轨迹及运动状态

图9给出了采用非线性反馈控制器后机器人运动轨迹与运动状态关系。

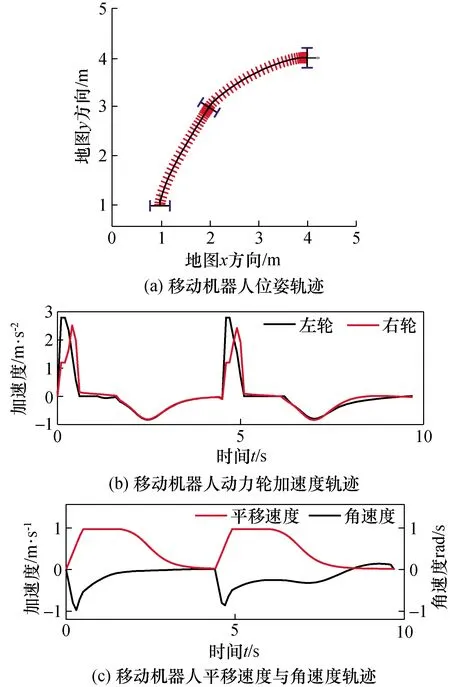
图9 采用非线性反馈控制器后机器人运动轨迹Fig.9 Motion trajectory of the mobile robot with nonlinear feedback controller

图10给出了采用快速限幅非线性反馈控制器后机器人运动轨迹与运动状态关系。从图9和图10可以看出采用快速限幅非线性反馈控制器后机器人具有更加平滑的全向运动轨迹。

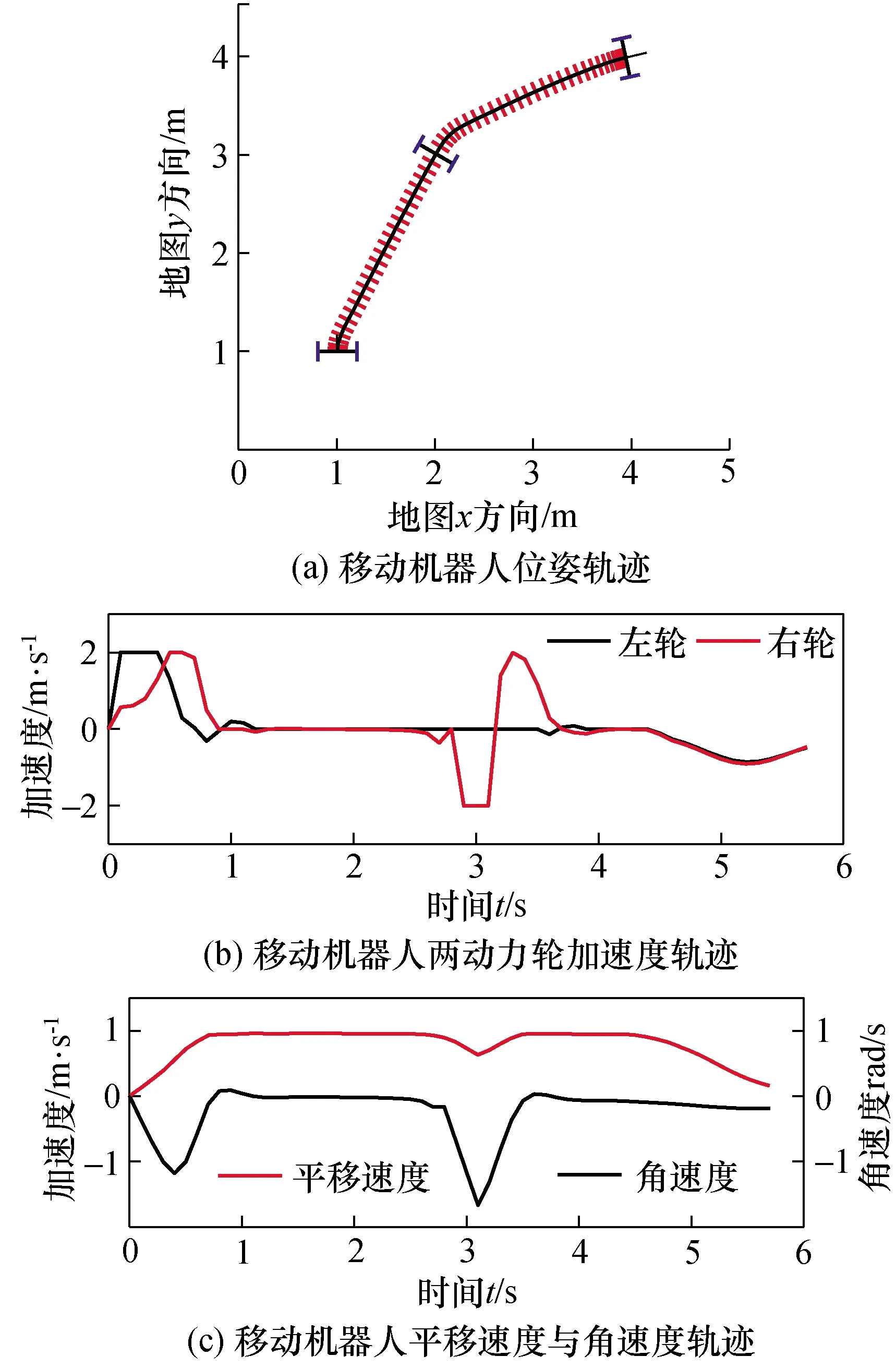
图10 采用快速限幅非线性反馈控制器后 机器人运动轨迹Fig.10 Motion trajectory of the mobile robot with fast limiting amplitude nonlinear feedback controller

5.2 机器人路径规划

为了验证提出算法的可扩展性能。本文采用与RRT算法相关的改进算法相同的扩展方式，算法编号与对应算法见表1。

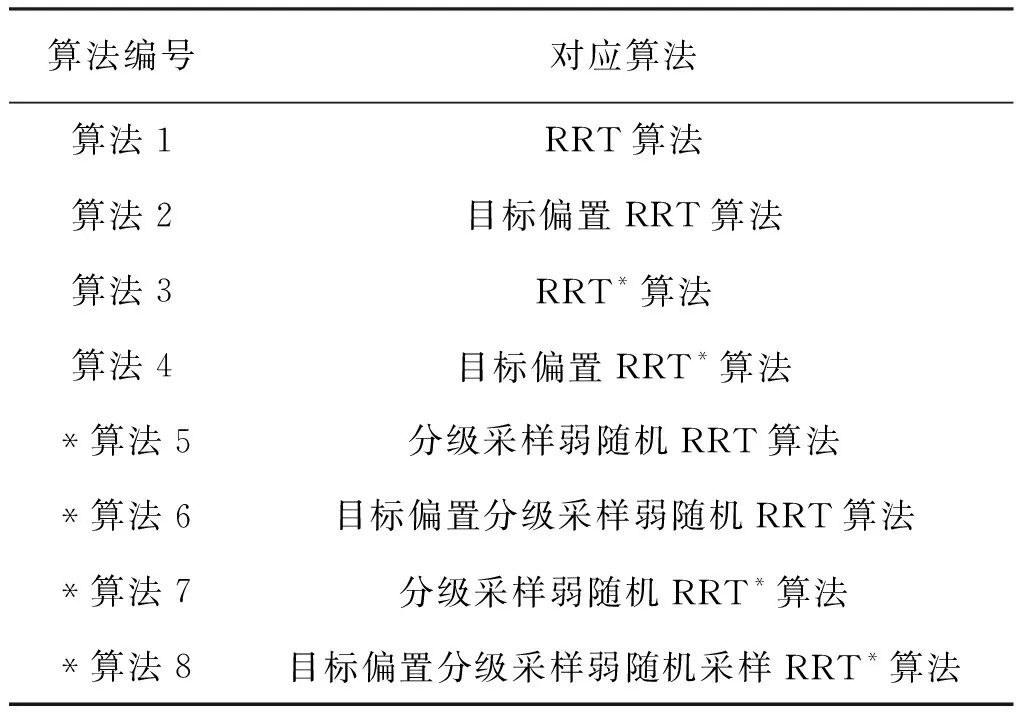
表1 算法编号与对应算法Tab.1 Algorithm number and corresponding algorithm

表1中的算法1～4为RRT算法及其改进算法，算法5～8为本文提出的算法及在其基础上扩展的算法(有*标记)。同时设计3种不同场景地图环境对相关算法进行仿真验证,地图大小为200 m×200 m。

环境(1):简易障碍物场景

图11表示简易障碍物环境下仿真结果。

从图11(a)可以看出,在简易障碍物测试场景中，原始RRT与分级随机采样的弱随机RRT算法均规划出了一条无碰撞的路径。

从图11(b)可以看出，采用分级随机采样弱随机RRT算法求解得到的时间区间更小，稳定性更好。

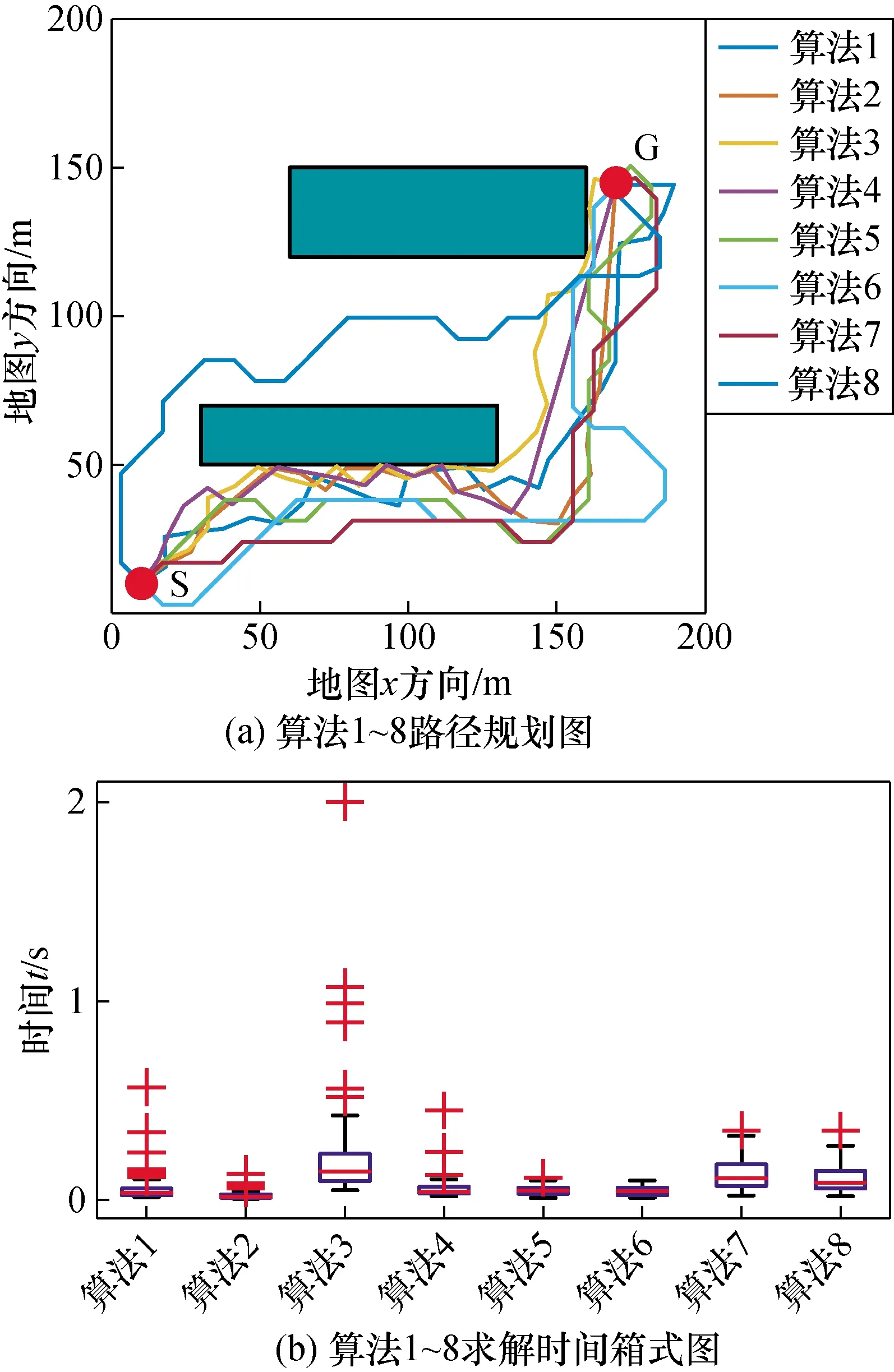
图11 简易障碍物环境仿真结果Fig.11 Simulation results in simple obstacle environment

环境(2)：杂乱障碍物场景

图12表示杂乱障碍物环境仿真结果。

从图12(a)中可以看出，各算法在面对杂乱障碍物场景，仍然可以完成规划任务。由于障碍物的增加，规划任务难度的增强，需要迭代的次数也随之增加，分级随机采样弱随机RRT算法效率更高。

从图12(b)中可以看出，采用分级随机采样弱随机RRT算法求解区间更小，同时缩短了求解时间。

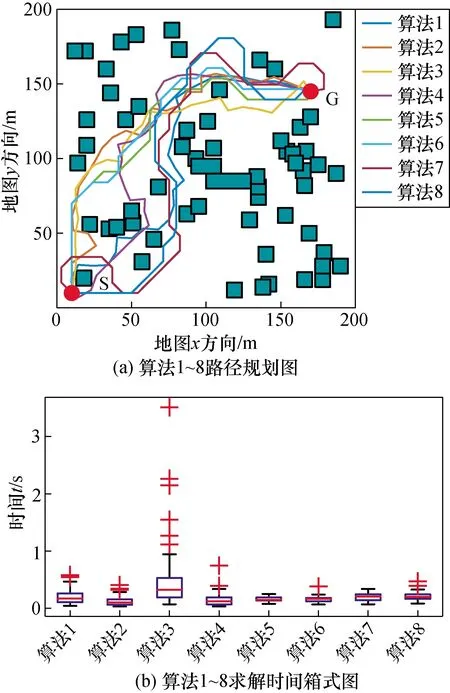
图12 杂乱障碍物环境仿真结果Fig.12 Simulation results in messy obstacle environment

环境(3)：室内狭窄通道场景

图13表示室内环境狭窄通道仿真结果。

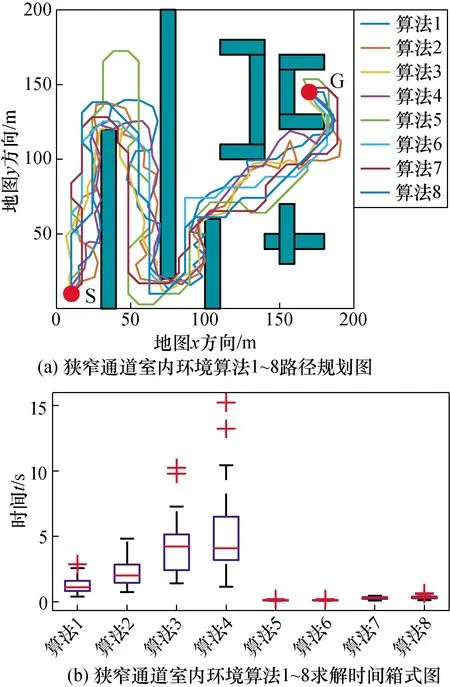
图13 室内环境狭窄通道仿真结果Fig.13 Simulation results in narrow channel of the indoor environment

从图13(a)中可以看出，各个算法完成了指定的规划任务，但由于通道狭窄，算法迭代次数增加，RRT的求解速度降低;分级随机采样弱随机RRT算法缩短了求解时间，提高了迭代速度。

从图13(b)中可以看出，采用分级随机采样的弱随机RRT算法求解速度更快，效率更高。

对基于分级随机采样的弱随机RRT算法在上述狭窄通道室内环境中的原始路径进行冗余节点裁剪与转向节点附近多次采样，降低原始路径的长度与节点数。根据移动机器人动态约束，移差速轮速度与加速度均不能超过最大值，且移动机器人仅通过调节两动力轮来控制其运动状态，为了更接近移动机器人实际的运动状态，仅设置最大速度为vmax=1 m/s，最大加速度为amax=2 m/s2。参数设置为Kρ=1,Kφ=-1,Kα=6,Kv=2。

图14为室内环境狭窄通道运动规划仿真结果。

图14 室内环境狭窄通道运动规划仿真结果Fig.14 Simulation results of the motion planning in narrow channel of the indoor environment

从图14(a)可以看出，采用快速限幅非线性反馈控制器无需将原始轨迹转进行光滑处理，就可以对移动机器人进行位姿规划，最终生成连续光滑的轨迹，且误差范围更小。经过转向后，移动机器人收敛于终点，且速度衰减值0。

从图14(b)、图14(c)和图14(d)中可以看出，采用快速限幅非线性反馈控制器在对机器人进行转向和角度控制时，机器人始终满足物理模型动态约束，其原因是两动力轮的速度和加速度都不超过物理模型规定的最大值。

6 结 论

本文将RRT算法先产生随机点，再搜索父节点的扩展方式，改进为先选择扩展的父节点，再随机确定扩展方向，最后计算得到子节点，完成迭代。避免了算法迭代后期，搜索父节点产生的计算量大的问题，获得了更小的求解区间与更快的求解速度。此外，针非线性反馈控制器在移动机器人运动规划过程中，忽视差速轮加速度，致使差速轮的加速度在转向时不受移动机器人物理模型约束的问题，提出将非线性反馈控制器得到的差速轮速度作为差速轮期望速度，通过快速限幅得到实际的差速轮加速度，进而保证运动规划过程中转向函数始终满足系统模型动态约束。最后通过仿真验证提出方法的有效性。仿真结果表明分级随机采样弱随机RRT算法具有更快的搜索速度与收敛速度。后续工作将考虑提升算法初始解的质量，实现动态环境下移动机器人的运动规划。